Review

, Volume: 7( 2) DOI: 10.37532/2320-6756.2019.7(2).176

• View PDF
• Download PDF

The Postulate of Equivalence Masses or the Law of their Proportionality?

*Correspondence:

Andew Chubykalo Unidad Académica de Física, Universidad Autónoma de Zacatecas, AP C-580, Zacatecas, México, E-Mail: achubykalo@yahoo.com.mx

Abstract

The main sources of GTR problems are analyzed. First, physicists and geometers in explaining phenomena do not take into account the simultaneous existence of two spaces (linear space-time and curvilinear space-time). Secondly, it is shown that the initial postulate on the equivalence of inertial and gravitational masses is erroneous from the point of view of philosophy and physics. Moreover, experimental testing of the hypothesis is difficult because of the lack of accuracy of the measuring devices. It is shown that gravity can be considered as a quadratic effect of electrodynamics. The postulate on the equivalence of inertial and gravitational masses must be replaced by the law of proportionality of the inertial mass of the body and its gravitational charge. The new approach fits in perfectly with the idea of J. Thomson on the electromagnetic nature of material bodies.

Keywords

Electromagnetic mass; Newton’s law of universal gravitation; general theory of relativity

PACS numbers: 03.50.-z; 03.50.De

Introduction

The idea of the electromagnetic nature of inertial matter was put forward at the end of the 19th century by the great English scientist Thomson. Electromagnetic mass is

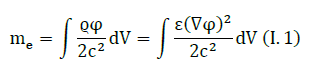
However, the development of this idea was hampered by the following circumstance. The law of conservation of energy formulated by Poynting was limited by electromagnetic waves and was completely unsuitable for instantaneous fields of inertial charges.

The problem of electromagnetic mass in the nonrelativistic approximation was solved only after proving two new energy conservation laws: the Umov conservation law and the Lenz conservation law [1]. Based on these laws, it was proved that the electromagnetic mass has the same properties as the standard inertial mass. Umov’s conservation law in relativistic-covariant form was formulated later (see, for example, [2]). The results obtained allowed to solve a number of important issues. The relativistic Lagrange function describing the interaction of electric charges with each other was strictly justified. The theory of interaction fit perfectly into the framework of relativistic and classical mechanics [2]. However, Newton’s law of world gravitation has not yet had an electromagnetic explanation.

Newton’s law was, as it were, beyond J. J. Thomson’s idea. The problem of explaining Newtonian gravity from the position of electromagnetism had a logical difficulty. Large bodies (stars, planets, material objects) are electrically neutral. How can we relate electric charges and the phenomena of mutual attraction of neutral bodies?

To explain the phenomena of A. Einstein created GTR, which is constantly criticized. A number of papers were published in journals with an analysis of the difficulties of GTR and a critique of the physical interpretation of phenomena in GTR [3-6]. “Black Holes”, “Dark Matter”, “Big Bang” and other oddities of the phenomena predicted by GTR, demanded logical explanations. Finding the source of the problems led us to discover an interesting fact. The fact is that about 200 years ago geometers made a mistake [7].

The essence of the error is simple. We can construct a curvilinear space-time only using Euclidean space and classical time. Geometers and theorists acted simply: they built a curvilinear space-time in a linear space-time, setting the metric tensor in a classical space-time With further analysis, physicists and geometers "safely forgot" about the original linear space-time. They built explanations as if the classical space-time does not exist. In this regard, there is a difficult problem of correcting errors and finding new explanations for the GTR phenomena. This is a very difficult task, in our opinion. Until this problem is solved, we cannot consider GTR as a scientific theory.

• In addition, Einstein’s idea of the equivalence of inertial and gravitational masses seems to be erroneous from the point of view of materialistic philosophy¹. This is the second problem that does not allow to recognize GTR by scientific theory. Below we look at the equivalence problem

Proportionality or Equivalence?

In nonrelativistic mechanics there are two concepts of mass: the first relates to the second Newton’s law, and the second to the law of Newton’s gravitational force:

The first mass, inertial, is the ratio of the force of gravity acting on the body to its acceleration.

The second mass, gravitational, determines the force of attraction of the body by other bodies and its own force of attraction.

These two masses are measured in different experiments, so they are absolutely not obliged to be connected, and even more so to be proportional to each other.

In modern physics, the opinion was strengthened that the strict proportionality of these masses was established experimentally. Note, moreover, that in [8], in the framework of classical mechanics and Euclidian geometry, it was theoretically proved that the principle of proportionality of inertial and gravitational masses holds for two interacting neutral (having no any electric charges) bodies. This allows us to speak about a single body mass, both in non-gravitational and gravitational interactions. A suitable choice of units can make these masses equal to each other. "Strong proportionality" can have several explanations. There are two models that use different principles:

• The law of proportionality of the masses: The first model states that inertia and gravity are various phenomena that are not related to each other, which may have a common nature. However, due to some properties of a substance, the proportionality between masses takes place in a wide range of conditions. The rule has limits of applicability beyond which it is violated

• The equivalence postulate of the masses: Creating GTR, Einstein proposed to quantitatively equate inertial and gravitational masses. From a philosophical point of view, this hypothesis is untenable, since quantitative equality inevitably leads to the identification of qualitative properties. Therefore, in physics, there is a statement that the gravitational and inertial forces not only have a common nature but also the same

The two approaches indicated are fundamentally different. We need to discuss the characteristics of each approach. From the point of view of experimental verification, both approaches are equivalent. Therefore, the statement of the mass equivalence postulate automatically confirms the principle of mass proportionality. It was experimentally confirmed that the principle of proportionality between inertial and gravitational masses takes place for two interacting bodies [9,10]. Proportionality was theoretically proved in the interaction of two electrically neutral bodies within the framework of classical mechanics[8]. Experimental testing of Einstein’s hypothesis using only two bodies is impossible. Looking for new ideas.

We can offer a direct way to test the mass equivalence hypothesis. In classical physics, there is the principle of “independence of pair interactions”. Two objects interact with each other, regardless of their personal interaction with other bodies.

The interaction of the three bodies: As an illustration of the verification method, we consider the interaction of the Sun with the Earth-Moon system. We will write the Lagrange function for this system.

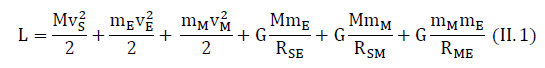
where M is the Sun mass,v_S is the Sun velocity, m_E is the Earth mass,v_E is the Earth velocity, m_M is a mass of the Moon,v_M is the Moon velocity, R_SE is the distance from the Earth to the Sun, R_SM is the distance from the Sun to the Moon and R_ME is the distance from the Earth to the Moon.

The solar mass M interacts with two masses m_E and m_M. This is the gravitational mass of the Earth and the gravitational mass of the Moon. If, say, the Earth and the Moon are far apart, then the energy of interaction between them is small. However, even this low interaction energy W corresponds to some inertial mass

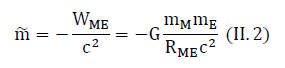
The sign “–” in the formula is due to the fact that the interaction energy is negative. If the principle of mass equivalence holds, then the Sun should have a gravitational interaction with this mass. However, in the framework of classical mechanics, such an interaction does not take place due to the principle of independence of pairwise interactions.

So, we have come to the possibility of direct experimental verification of the equivalence principle. It is necessary to establish: does the mass 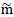have gravitational properties or not²?

In a series of experimental studies, we did not find a similar formulation of the question. The estimate shows that to establish the gravitational properties of the mass 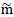, very high accuracy is required (above 10^-17). Now we can say that the principle of mass proportionality has good experimental confirmation. However, the principle of mass equivalence, proving the equivalence of gravity and inertia, has not yet received experimental confirmation or experimental refutation.

The Square Effect of Electrodynamics

As we wrote earlier, The great scientist Thomson drew attention to the analogy between the Quasistatic phenomena of Electrodynamics and Mechanics. He expressed the idea of the Electromagnetic nature of material objects with inertia. We will continue to develop the Thompson idea and show that Gravity is a quadratic effect of Electrodynamics.

Indeed, if we write down the Coulob's Law for static charges and the Newtonian Law of Universal Attraction, then the similarity of the law is surprising. we write the Lagrange functions:

1. Coulomb’s law

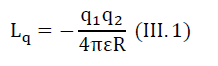
2. The law of universal attraction

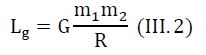
Further, it is possible to generalize the Lagrange function to the case of relative motion of charges, when the electrostatic potential in L_q depends on the relative velocity of charges. We write the Lagrange function for this case.

Coulomb’s Law with Potentials Depending on the Relative Velocity of Charges v₁₂[2]:

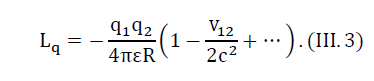
Using the principle of similarity, we can write the generalized Lagrange function for the expression (III.2):

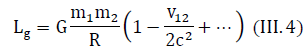
We note that the results of calculations by formula (III.4) coincide with the results of special relativity if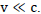

To avoid ambiguous interpretation, we first consider the quadratic effect on the example of a single charged particle, the proton. Below we write the Lagrange function for the interaction of two protons (III.3), adding to it quadratic terms:

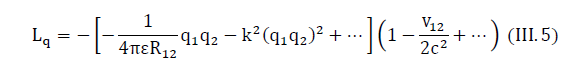
where q₁,q₂ are the charges of the first and second protons, R₁₂ is the relative distance between protons,v₁₂ is the relative velocity of protons, k² is the proportionality factor.

So, we have an expression that allows us to show the electromagnetic nature of Newtonian gravity. Using expression (III.5), we write the formulas for each member of the sum in square brackets separately:

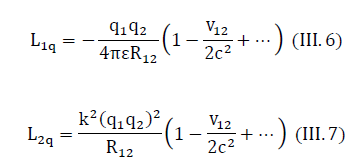
Expression (III.7) is very similar to the Lagrange function for Newton’s law of global attraction (III.4).

Expressions (III.4) and (III.5) will coincide if we assume that the gravitational charge of the particle is proportional to the square of the electric charge of this particle q² Historically, there is a tradition when inertial and gravitational masses have the same units of measurement (kilograms (SI)). We will keep this tradition. To distinguish the gravitational mass from the inertial mass of the proton, we replace the value m_P with a numerically equal value m_P^* is the gravitational charge of the proton.

Note: We hypothesize that the coefficient k is a universal constant for the charges of any elementary particles. The relationship between the inertial mass and the gravitational charge for complex objects (ions, atoms, massive bodies, etc.) can be determined based on the patterns that will be established below for elementary particles.

To avoid further confusion in terminology, we will only talk about the inertial mass of the particle and the gravitational charge of the particle. The term gravitational mass, we will not use.

The Interaction of Two Protons

Large inertial masses (for example, planets) do not have an excess charge. They are electrically neutral. To establish a connection with neutral bodies, we will continue the analysis from the study of the gravitational interaction of two charged particles, protons. For simplicity, we assume that the relative velocity of the interacting bodies is zero.

So that between expressions (III.4) and (III.7) there is an identity, the corresponding members must be equal:

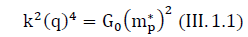
where G₀ is the gravitational constant of protons.

The gravitational charge m_P^* is proportional to the square of the electric charge and is always positive. The proportionality coefficient k is a constant value for a proton equal to:

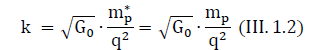
We know the magnitude of the proton charge, the mass of the proton and the gravitational constant. Therefore, we can calculate the value of the constant k. The physical constant k is universal for all elementary particles, as we wrote above.

The unit of measurement of the gravitational charge of the proton and its inertial mass is, as we said, the kilogram (SI). It remains to recall that the inertial electromagnetic mass of the resting charge is equal to:

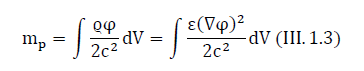
In accordance with the established tradition, we chose the units of measurement so that the ratio of the gravitational charge of the proton to the inertial mass of the proton is always 1 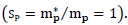In nature, there are, as is known, other particles (electrons, ions, neutrons, neutral atoms, and molecules, etc.). we will look at them in the following paragraphs. proton will serve as a benchmark for comparison.

In nature, there are many charged and neutral particles. We must find a common approach to the description of gravitational interactions between them. Above, we described a proton and obtained the constant k formula (iii.1.2). The constant k, like G₀ is a universal physical constant for all elementary inertial particles. Knowing the magnitude of the charge, we can calculate the magnitude of the gravitational charge for any elementary particle.

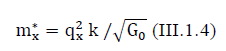
where m_X^* the desired gravitational charge of the particle , q_X² is the square of the particle charge x.

We draw readers’ attention to the differences between the gravitational charge of a charged elementary particle m_X and its inertial electromagnetic mass m_X The gravitational charge m_X^* (see expression (III.1.4)) has no direct connection with the inertial electromagnetic mass m_X defined by expression (III.1.3). The gravitational charge m_X^* and the inertial electromagnetic mass m_X reflect the different properties of the elementary particle. Therefore, we have no right to talk about the “equivalence” (identity) of these masses. Now we can proceed to the determination of the gravitational charge of other elementary particles.

• Electron: The inertial mass of the electron is 1/1836 of the inertial mass of the proton. The electric charge of an electron is equal to the electric charge of a proton. If we calculate the gravitational charge of the electron using (III.1.4), then it turns out that it is numerically equal to the gravitational charge of the proton. For an electron, the ratio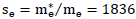

• Neutron: From the point of view of the quadratic effect, the neutron is a special particle, because it does not have a pronounced charge. We study macroscopic phenomena, so we do not need to consider the quark model of a neutron. It is important for us to bear in mind the following experimental fact. The difference of inertial masses between the proton and the neutron is small by the standards of nuclear physics and is about 1.3 MeV. As a result, the neutron in the nuclei may be located in a deeper potential well than the proton, and therefore the beta decay of the neutron is energetically unfavorable. This leads to the fact that the neutron in the nuclei can be stable

Moreover, in neutron-deficient nuclei, a beta transition of a proton into a neutron occurs with the capture of an orbital electron. For this reason, from a macroscopic point of view, we can conditionally consider a neutron as a “bundle” of a proton and a neutron with a relatively weak electrostatic interaction of electric charges. Following this logic, we can assume that the gravitational charge of the neutron is the sum of the gravitational charge of the proton and the gravitational charge of the electron. In other words, the gravitational charge of a “neutral” neutron is twice as large as the gravitational charge of a proton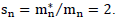

The proportionality law (neutral objects)

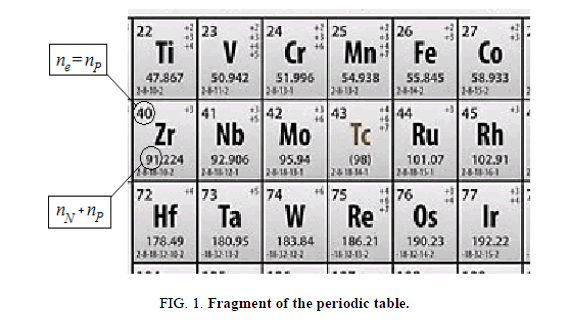
Consider the periodic table (FIG. 1). In each cell occupied by a chemical element, there are two numbers. In fig. 1 upper digit indicates the ordinal number of the element. It reports the number of protons (or electrons) in a neutral atom 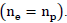The bottom number indicates the atomic mass of the element. Atomic mass is a dimensionless quantity. It is defined as the ratio of the mass of an atom of a given element to 1/12 the mass of a neutral atom of the carbon isotope 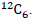For any isotope, atomic mass is an integer. It is equal to the sum of neutrons and protons in a given isotope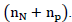

Earlier we established the same dimension of gravitational charges and inertial masses. Therefore, we can use dimensionless units of atomic masses.

Each cell of the table has a sequence number of an element equal to the number of protons (electrons) in a neutral atom of this element. The table also indicates the relative atomic mass (weight) of this element. The atomic mass of an isotope is numerically equal to the sum of the number of neutrons and protons 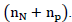Now we can refer to the periodic table and select any element from this table. As an example, choose zirconium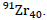

The inertial mass of the zirconium atom is numerically equal to the sum of the mass of protons, electrons, and neutrons. In our case, the inertial mass of the proton is 1, the inertial mass of the neutron is also approximately equal to 1, and the inertial mass of the electron is 1836 times smaller than the mass of the proton. So, the inertial mass of zirconium 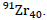in atomic units is equal to:

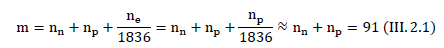
The contribution of electrons to the total inertial mass is negligible.

• Zirconium 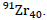gravitational charge: As we established earlier, a proton and an electron have the same opposite electric charges. The gravitational charge of the proton is 1, and the gravitational charge of the electron is equal to the gravitational charge of the proton, i.e. also equal to 1. The gravitational charge of the neutron is equal to 2. It is easy to calculate the gravitational charge of a neutral zirconium atom (atomic units),

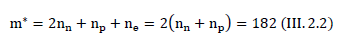
It is interesting to note that 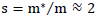not only for any neutral element of the periodic table. Expression 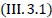reflects the proportionality of inertial mass and gravitational charge for any neutral massive bodies (solids, liquids). Expression 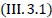does not depend on the chemical composition, shape and size of a neutral object. The reason is that the contribution to the total energy of the binding energy of the chemical compounds of atoms due to the interaction of ions of a solid or liquid substance with each other is very small and is a fraction of a percent.

• Gravitational constant 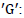Scientists measure the gravitational constant using Newton's law and electrically neutral masses. This law includes inertial masses, and not gravitational charges proportional to them. We must find the gravitational constant 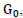using the expression 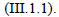If in this law for electrically neutral bodies replace the inertial mass of the proton by the gravitational charge, then we get:

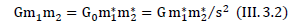
where 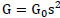is the gravitational constant measured experimentally for neutral bodies; G₀ is the gravitational constant for the proton, m₁=m₂ are proton masses, 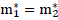are gravitational charges of protons. Since for neutral bodies, the ratio is s=2 the experimentally found value of the gravitational constant G and the proton constant G₀ can be calculated using the formula

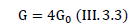
Taking into account the expression 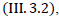Newton’s universal law for gravitational force in the interaction of neutral bodies has the following form

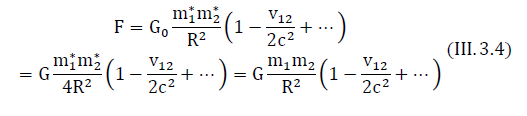
It completely coincides with Newton’s famous law. So, we have obtained an important law of proportionality for any neutral bodies. With the selected system of units of measure, the ratio of the gravitational charge of a neutral body to its inertial mass is a constant value approximately equal to 2.

The inertial mass of the neutral body is the sum of two masses. The first mass is a positive mass. Its value is the sum of the electromagnetic masses of the body charges. The electromagnetic mass of the charge is determined by the expression (III.1.3). The second mass is due to the gravitational interaction and has a negative value. Its value is associated with the gravitational interaction of atoms with each other. Obviously, the negative gravitational mass is negligible.

Here we have the right to continue the analogy between the electrostatic charge with its potential and the gravitational charge with its potential. However, these questions require a separate presentation.

The proportionality law (charged objects)³

Considering the proton, we found that for the proton the value 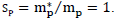For electrons 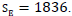Another example of exclusion from the law of proportionality 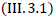is any ion. As an example, consider the -particle. This is a double-ionized helium atom He⁺⁺. For an -particle, the value of s is equal to

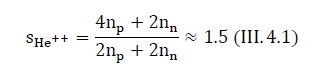
Thus, ionized molecules do not obey the mass ratio (III.3.1). Each ion has its own coefficient depending on the degree of ionization.

In general, Newton’s universal gravity law takes the following form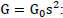

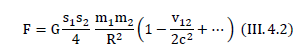
We see that the law of Newton (III.3.4) must be “corrected” for charged interacting objects. This correction is written by the factor 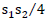in the law of universal gravity (III.4.2). So, “maxwellization” of the equations of gravity allowed us to describe a new model of the physical nature of gravity. Newton's law of universal gravity is preserved, but the phenomena have a different explanation.

• "Atmosphere" of the sun: Now we can illustrate the structural features of the solar "atmosphere" based on the results obtained. Suppose that different particle fly out at the same speed and stop under the action of the forces of gravity of the sun. The particles have the following lift heights (conventional units):

These results allow us to describe qualitatively the structure of the solar atmosphere. First of all, we note that the kinetic energy of electrons is much less than the kinetic energy of alpha-particles, hydrogen atoms, and helium. Their energy is too low to overcome the forces of gravity. For this reason, it can be assumed that a relatively “thin” layer of electrons with a fairly high concentration can exist on the surface of the sun. As the distance from the sun increases, the electron concentration will decrease. The place of electrons will replace a wide layer of neutral particles (atoms of hydrogen, helium, etc.) With “interspersed” positive ions. Part of the neutral particles stops and returns to the sun. This layer as the distance from the sun will be replenished with positive ions of helium, hydrogen, etc.

The concentration of neutral particles near the surface of the sun has a large density gradient. Therefore, the light, passing near the surface of the sun, changes direction, i.e. Rays of the light bend.The next extended region is an area with a large number of positive ions. Planets move in the field of charged particles. Due to the deposition of ions on the surface of the planets, the planets always acquire a small electrical charge. If the total charge of a thin “electron shell” near the sun is several hundred coulombs, then between the charged planet and the electron “shell” of the sun there is a Coulomb interaction that must be taken into account.

It is especially important to take these phenomena into account when assessing the effects of solar flares on the motion of the planets. With an increase in the alpha particle flux, the radius of the planet’s trajectory slightly increases, the duration of the day on the planets changes, etc. The Coulomb forces can give tangible corrections to the results of experimental measurements.

Conclusion

So, the analysis showed the following:

1) Einstein’s postulate does not have a reliable experimental confirmation or refutation. However, mathematical analysis [6] helped to detec t the error of geometers in the GTR, which was made more than 200 years ago. It is necessary to correct the detected error. This means that the modern interpretation of GTR phenomena is not scientific. It needs to be revised

2) We found out that from a philosophical point of view, the postulate on the equivalence of inertial and gravitational masses is not justified. Inertia and gravity can have a common nature. However, they are a manifestation of various independent properties inherent in matter

3) We found that the phenomenon of gravity can be explained based on electrodynamics. At the same time, the law of proportionality between inert and gravitational for neutral masses is perfectly fulfilled. This proportionality does not depend on the chemical composition of the substance, on its size and shape

So, the idea of the great English scientist Thomson on the electromagnetic nature of weighty matter was further developed. Newton’s gravity can be considered as a quadratic effect of electrodynamics.

Acknowledgment

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

¹Analysis of the postulates of A. Einstein showed that he also made philosophical mistakes.

²Here we are dealing with the following strange facts. First, according to the principle of mass equivalence, all inertial and gravitational masses must have the same sign. The mass ? violates this condition because it is negative. Secondly, according to the classical rule of independence of pair interactions, the mass ? should not interact with the mass of the sun. Unfortunately, such “minor”, but fundamental problems of physics avoid discussing.

³We do not consider here the Coulomb interaction between the charges. Coulomb interaction is described in any textbook of physics. We are only interested in the effect of particle ionization on gravitational effects.

References

1. Kuligin VAV, Kuligina M, Kornneva M. The electromagnetic mass of a charged particle. Apeiron. 1996;3:7.
2. Chubykalo A, Kuligin V. Unknown classical electrodynamics. BJMP. 2018;4:384-425.
3. Arteha S. On the basis for general relativity theory. Spase Time and Substance. 2002;3:225-33.
4. Arteha S. Critical remarks to the relativity theory. Spase Time and Substance. 2005;6:14-20.
5. https://creation.com/light-travel-time-a-problem-for-the-big-bang.
6. Chubykalo A, Kuligin V, Espinoza A. Spatial curvature as a distorted mapping of Euclidean space. BJMP. 2018;4:435-42.
7. Will C. The Confrontation between General Relativity and experiment living. Rev Relativ. 2006;9:3.
8. Chubykalo A, Vlaev S. Theorem on the proportionality of inertial and gravitational masses in classical mechanics. Eur J Phys. 1998;19:1-6.
9. Turyshev S. Experimental tests of the general theory of relativity: recent advances and future directions of research. UFN (Uspehi). 2009;179:3-34.
10. Turyshev S, Shao M, Girerd A, et al. A search for new physics with the BEACON mission. Int J Mod Phys D. 2009;18:1025-38.