Short communication

, Volume: 7( 1) DOI: 10.37532/2320-6756.2019.7(1).169

• View PDF
• Download PDF

The Electromagnetic Field of a Magnetic Dipole above a Conducting HalfSpace

*Correspondence:

Seliem Aasa Department of Mathematics, Faculty of Science, University of Kafr El-Sheikh, Egypt, E-Mail: adel_atta60@yahoo.com

Abstract

We calculate solutions for the electromagnetic field due to a magnetic dipole and a finite loop vertically oriented and above a conducting ground by means of an approximate Green function in the frequency domain. Our solution is expressed as the sum of two partial azimuthally electric field, the two partial field are identified as radioactive and diffusion, the transient source in which the exciting current is abruptly switched off has been considered in detail.

Keywords

Reflection; Electromagnetic field; Ward

Introduction

The present paper is concerned priming with the asymptotic representation from the Fast Electric Maniac (FEM) above a uniform conducting ground and scattered form are bodies within the ground, the paper interpretation of their results requires the development of theoretical models as has been started by Wait JR and Kaufman AA [1,2]. The electromagnetic field due to current loop is naturally described by a magnetic Hertz vector while the elementary source is a magnetic dipole. The solution of the present boundary vale problem, where the field derived a vertically oriented distribution of magnesium above the horizontal interface of the air, and the ground is the solution. Stration considered the electromagnetic theory as section 1 [3], and Ward in his study concluded that a ward loop may be regarded as equivalent to the distribution of magnesium [4-6]. We consider the transient field resulting from an abrupt current and showed that the radioactive field is a superposition of poles using the intranet of the element of tangle in the ground [7].

The diffuse field is essentially more complex, we restrict our investigation to its structure and above the ground and lies enough for an asymptotic approximation as an application [8]. Further, since the field is continuously ensured using a recurring loop at the same height, we restrict our calculation to the field of the height.

Methods

The source of magnetic Hertz vector 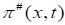of the distribution of magnetization M(x, t) in accordance with the vector equation of wirlas wireless telegraphy

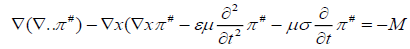(1)

In a medium specified by its uniform permeability, permittivity and conductivity, the electric and magnetic field vectors E(x,t) and H(x,t) are given in terms 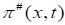by formula:

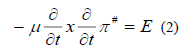
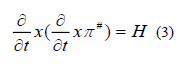
In air, we take 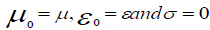so that equation reduced to the simpler form of the wave equation, in the ground, we take 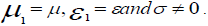To satisfy the boundary conditions, the magnetic tangent component of E and H are continuous. For the horizontal loop, both 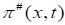and M are parallel to unit vector k to which we take:

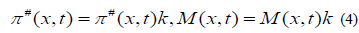
With the origin on the surface of the ground, the boundary condition reduced to the form

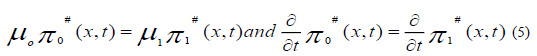
On z=0 where we have taken z=x-h by applied the Fourier transform, it is convenient to eliminate time derivatives

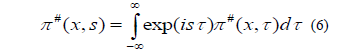
Subtitled from equation (2) and (3) transforms into the scalar Helmholtz form

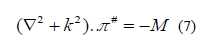
Where,

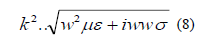
The solution of the last equation subject to boundary conditions of the (5) is approximately expressed in medium terms of the Green function 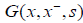corresponding to a unit source at a point x and the same boundary condition. Thus for any distribution M (x,s), we have:

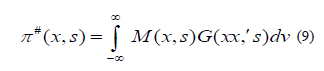
Where the integral is to cover the whole of space and

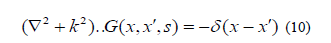
Substitutimg the same boundary condition transform of the field vectors are this given by the formula:

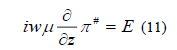
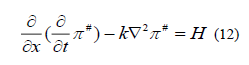
We are interested in the particular case, when the source 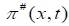is a finite horizontal loop of radius ‘a’ carrying the current ‘I’ (t) at height ‘h’ above the ground taking the origin of the coordinate vertically below the loop, we have

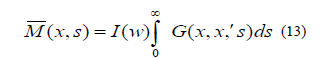
Where ‘c’ the integration is over the plane surface spinning the loop. The transforms of the field vectors can readily be obtained by substitution from (4) into (11) and (12) together with the application of Stokes theorem to the surface integral

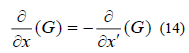
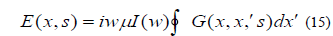
Where the integration is around the loop, in the right-hand sense with respect to direction K. The Gamma function to the position can be Written in Sommerfeld form:

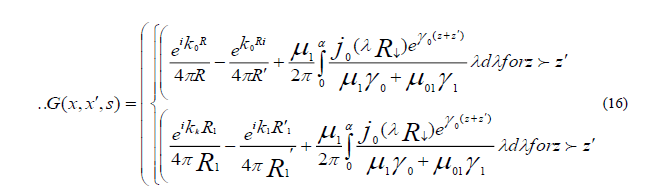
Where, 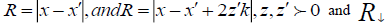is the magnitude of the horizontal component of both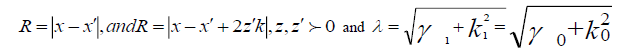

Corresponding to the value of k square in the air and the ground respectively and 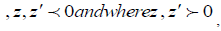respectively contributions from the unit source x and its image at 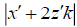have an integral representation of Euler form

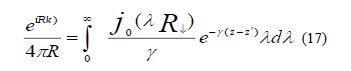
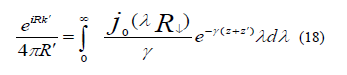
We took cylindrical polar coordinate 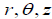corresponding to unit vectors and found E is independent of azimuth for having the d same direction of its interesting form. We derived the electromagnetic (emf) that would be introduced in the recurring loop, it is sufficient to investigate only the electric field due to the transmitted loop contained above the origin.

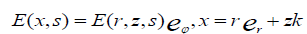
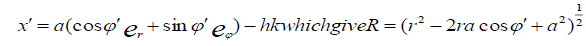
And,

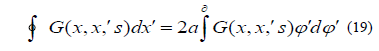
From the addition formula for the Bessel function, the results obtained are

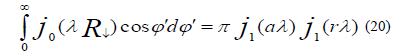
When we substitute from (15) into (14), we find

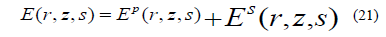
Where,

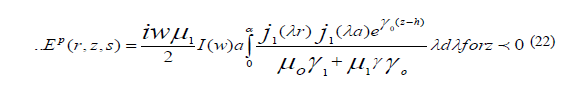
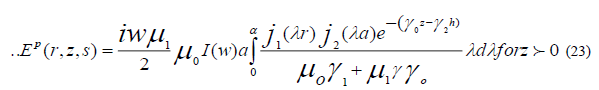
The corresponding result for an elementary dipole whose mount is of limiting values of 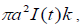first discussed by Wait JR [1], can be recovered from this formula by applying the approximations, thus, we get

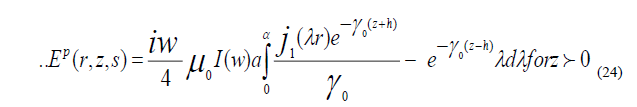
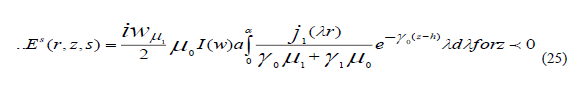
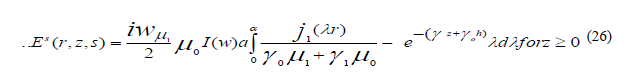
The results can be obtained directly from E an substituting 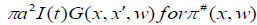the partial field corresponding E^p (r,z,s) is purely radiated vanishing when the source is on ground, whereas that corresponding E^s (r,z,s) is diffusive in character, because of its dependence on the conductive of the ground , they are given by inverse transforms , of the form

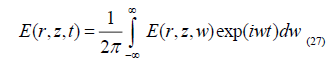
In general, such field cannot be determined in exact form, however, for h=0, the radiation component 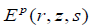is always zero owing to the coincidence of the source and image at the air-ground interface.

Conclusions

We consider the transient field resulting from an abrupt current, we show that the relative field consists of a superposition of Huygens spectral pulse issuing at the instant of a switch - off from each element of the source and image of the ground.

References

1. Wait JR. Electromagnetic waves theory. 1986.
2. Kaufman AA. Harmonic and transient field on the surface of non-layer medium. Geophysies. 1969;44:1208.
3. Stration JP. Electromagnetic theory. Mc.Graw-Hill. 1941.
4. Ward SH. Part A. Electromagnetic theory for geophysical applications. Mining Geophysics. 1967;2:13-196.
5. Ward SH. Part C-The electromagnetic method. Mining Geophysics, Theory. 1967;2:224-372.
6. Morce PM, Feshbach H. Methods of theoretical physics. Mc-Graw Hill. 1951.
7. Sommerfeld A. Partial Differential in physics. Academic Press. 1941.
8. Abo-Seliem AA. The transient response above an evaporation duct. J Phys D Appl Phys. 1998;3:3046-50.