Original Article

Received: June 6, 2018; Accepted: June 11, 2018; Published: June 18, 2018

Citation: Ucar E, Yakinci ME. Static and Dynamic of Vortex in Y₁Ba₂Cu₃O_{7- δ} Superconductor. J Phys Astron. 2018; 6(2):154

Abstract

In this study, static and dynamic of vortex have been investigated in Y1Ba2Cu3O7-δ system depending on the magnetic field and temperature. The Y1Ba2Cu3O7-δ system was fabricated under different heat treatments between 900-9200C for 24 h. using conventional solid-state reaction technique. Magnetic fields dependence of the magnetic moments in the Y1Ba2Cu3O7-δ single crystal M-H measurements were carried out for different temperatures (10, 20 and 30 K).Temperature dependence of the magnetic moments in the Y1Ba2Cu3O7-δ single crystal by applying constant 500 Oe magnetic field. Vortex lattice thermal fluctuations, magnetic fields and random pinning favour a liquid or a disordered glassy vortex state. The non-equilibrium states contain several types of plastic and elastic motion.

Keywords

Superconductor; Magnetic field

Introduction

A flux solid phase with vortices pinned or otherwise held in place and flux liquid phase where many vortices are unpinned or free to move, but dissipation. These two phases are separated by a melting line that is also called the irreversibility line T_irr. Flux creep can occur to its left and flux flow to its right [1].

Dependence of the trapped field on temperature could be the result of the surface screening effects [2], surface barriers [3-10], and the softening of vortices [11]. Surface screening effects prevent the vortex penetration into a superconductor. However, the surface screening effect weakens with an increasing temperature, allowing more vortices to be pinned in a superconductor.

When a small field is applied at low enough temperatures, the strong surface screening currents limit the vortex entry into a superconductor. In this case only a small number of vortices can penetrate into the bulk, and their pinning results in a small trapped field. Applying a higher magnetic field causes an increase in the trapped field accompanied by a shift of the maximum to a lower temperature. This is because the density of the trapped vortices increases and an increasing interaction between the vortices in the vicinity of the saturation line lead to a depinning of the vortices trapped by the random pinning centers [12].

The width of the magnetization loop is proportional to the persistent (irreversible) current density. The same is true for local magnetization loop, where this width is proportional to the current density and depends on the position of the measured point inside the sample. Most of the existing theories of the critical state predict a decrease of the current density with the increase of the vortex lines density due to interaction between vortices. In high-T_c superconductor the situation is further complicated by the giant flux creep, since most of the experiments have a macroscopic time window and probe quite a relaxed state [13].

At low fields the elastic barrier is lower than the plastic barrier and the collective creep model describes magnetic relaxation. However, at larger magnetic field plastic creep becomes a more favorable channel for magnetic relaxation. Importantly, the relaxation rate in this case increases with an increase of the magnetic field [13].

Experimental Details

5 gram Y₁Ba₂Cu₃O_7-δ sample, where 0.7565 gram (Y₂O₃), 2.6455 gram (BaCO₃) and 1.5990 (CuO) was prepared by the conventional solid-state reaction method. The powders were mixed in a mortar for 1-2 h under atmosphere and 1 gram Y₁Ba₂Cu₃O_7-δ sample was pressed into pellets under a pressure of 4 MPa. The pellet was placed in an α-alumina crucible and then heat treated from 200°C to 9000°C for 24 h in O₂ atmosphere. Small pieces of Y₁Ba₂Cu₃O_7-δ single crystal were cut from a bigger as-grown crystal with scalpels, and then shaped into rectangular prism under a microscope. The crystal rectangular prism was dimensions of 2.9×2.0×1.8 mm³.

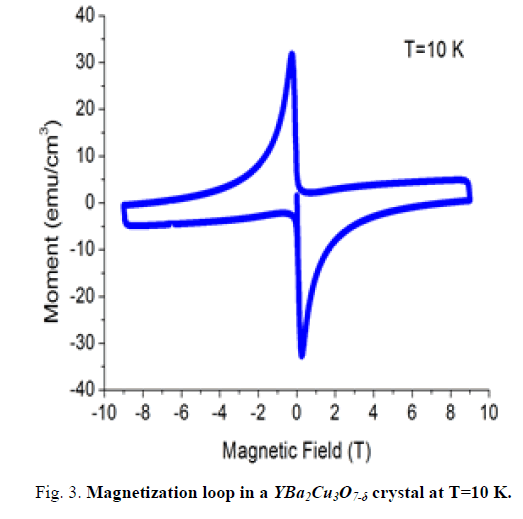
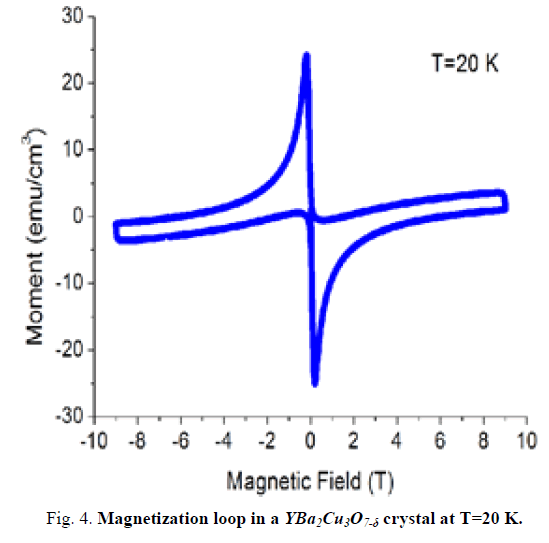
Magnetization measurements (M-T and M-H) of samples were carried out. (M-T) measurements were performed between 120 K and 5 K at a magnetic field of 500 Oe. Magnetic hysteresis (M-H) of samples was measured at three different temperatures, 10 K, 20 K, 30 K, up to the magnetic field of 8 T.

Results and Discussion

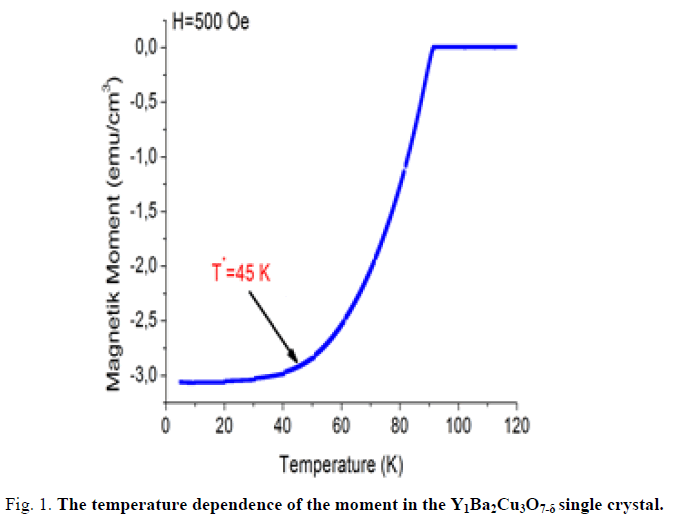
The highest Tc we obtained using the above stated procedure was 91 K as shown in FIG. 1. This is close to the Tc of Y₁Ba₂Cu₃O_7-δ single crystal 92 K.

Figure 1: The temperature dependence of the moment in the Y₁Ba₂Cu₃O_7-δ single crystal.

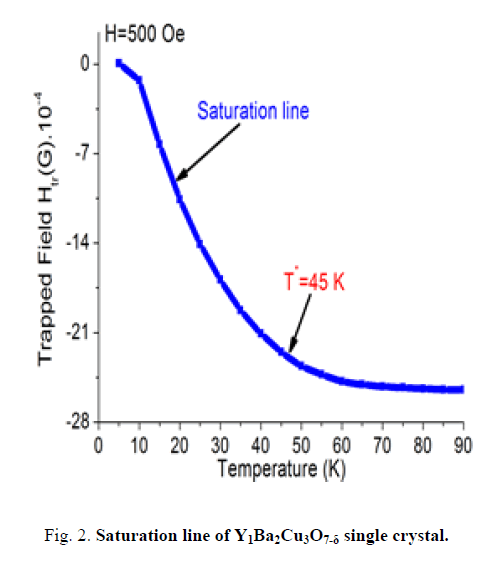
Studies have shown that Y₁Ba₂Cu₃O_7-δ superconductors have two vortex regimes at temperatures below and above the crossover temperature T0≈45 K as shown in FIG. 2. Each of these regimes has a different vortex dynamics and pinning mechanism.

Figure 2: Saturation line of Y₁Ba₂Cu₃O_7-δ single crystal.

In this study, we applied a constant 500 Oe external magnetic field, H, to a superconductor at different temperatures, which results in penetration of the vortices into the bulk of the superconductor. We then reduce T to 5 K and the vortex field trapped in the sample is detected. At or close to the melting field, the superconductor is fully penetrated and the internal magnetic field is expected to be constant over the entire sample volume. Therefore, the vortex structure close to the melting field can be well represented by the measurement of the trapped magnetic field.

The temperature dependence of the vortex melting line in the Y₁Ba₂Cu₃O_7-δ superconductor exhibits a crossover behavior as the temperature is decreased. Experiments have confirmed a very sharp drop of the melting field at as shown FIG. 2.

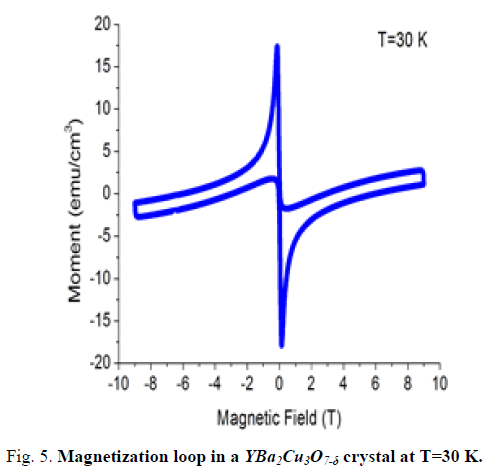
In this study, Magnetic fields dependence of the magnetic moments in the Y₁Ba₂Cu₃O_7-δ single crystal M-H measurements were carried out for different temperatures (10, 20 and 30 K). The magnetization exhibits hysteresis, that is, it depends on the external field was applied as shown in FIG.s 3,4,5. The width of the magnetization loop is proportional to the persistent (irreversible) current density. Decrease of the current density with the increase of the temperature due to interaction between vortices.

Figure 3: Effect of the column diameter on holdup.

Figure 4: Electropolarization curves of Sn₆₁Bi₂₅Sb₅Zn₄Al_3-XAg₂(TiO₂)_X alloys.

Figure 5: Intermodulation spectrum of Sn₆₁Bi₂₅Sb₅Zn₄Al_3-XAg₂(TiO₂)_X alloys.

At a fixed temperature, the trapped magnetic field increases with increasing external magnetic field and finally reaches a saturated value, which corresponds to the melting field. We name the temperature dependence of the saturation field as the “saturation line”. As the trapped field is monitored as a function of temperature, the behavior of the vortex lattice can be inferred. Our experiments have provided the experimental evidence for presence of theoretically predicted decoupling/depinning transitions in the vortex matter of Y₁Ba₂Cu₃O_7-δ superconductors.

Under the saturation line, the gradient of the magnetic induction (or density of flux lines) is sustained mainly by the elastic deformations of the vortex lattice. This means that displacements of the vortices out of the equilibrium positions are small.

Above the saturation line, however, the elastic deformations are not sufficient and usually the vortex lattice has many imperfections, such as dislocations and other topological defects. Therefore, there are usually several possibilities for the release of extra energy stored in a deformed (due to macroscopic vortex density gradient) vortex lattice. The first is via elastic accommodations, when the vortex jumps are not accompanied by a change of the local lattice structure. We will call it elastic creep. Another possibility is the plastic creep, which is realized via the motion of dislocations, jumps of interstitial vortices or (at large currents) channeling of vortices along the easy channels. The barrier for elastic creep is shown to increase with the increase of the magnetic field, whereas the plastic barrier (at least for single interstitial vortices and dislocations) decreases with an increase of magnetic field. This is because it is proportional to the inter-vortex distance 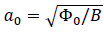[4].

Thus, at low fields the elastic barrier is lower than the plastic barrier and the collective creep model describes magnetic relaxation. However, at larger magnetic field plastic creep becomes a more favorable channel for magnetic relaxation. Importantly, the relaxation rate in this case increases with an increase of the magnetic field.

Conclusion

Thus, at low fields the elastic barrier is lower than the plastic barrier and the collective creep model describes magnetic relaxation. However, at larger magnetic field plastic creep becomes a more favorable channel for magnetic relaxation. Importantly, the relaxation rate in this case increases with an increase of the magnetic field.

References

1. Charles P, Poole, Jr.  Handbook of superconductivity. Department of physics and institute of superconductivity university of south carolina 2000:560;693.
2. Meissner W, Ochsenfeld R. Ein neuer effekt bei eintritt der supraleitfähigkeit. Naturwissenschaften. 1933;21:787-8.
3. Bean CP, Livingston JD. Surface barrier in type-II superconductors. Phys. Rev. Lett. 1964;12:14.
4. Burlachkov L. Magnetic relaxation over the Bean-Livingston surface barrier. Phys. Rev. B. 1993;47:8056.
5. Weir ST, Nellis WJ, Dalichaouch Y, Lee BW, Maple MB, Liu JZ, Shelton RN. Evidence for a time-dependent crossover from surface like to bulklike flux relaxation in YBa2Cu3O7− δ. Phys Rev B. 1991;43:3034.
6. Chikumoto N, Konczykowski M, Motohira N, et.al. Flux-creep crossover and relaxation over surface barriers in Bi2Sr2CaCu2O8 crystals. Phys. Rev. Lett. 1992;69:1260.
7. Zeldov E, Larkin AI, Geshkenbein VB, et. al. Geometrical barriers in high-temperature superconductors. Phys. Rev. Lett. 1994;73:1428.
8. Indenbom MV, D'anna G, André MO, et. al. Edge-shape barrier irreversibility and decomposition of vortices in Bi2Sr2CaCu2O8. Physica C. 1994;235:201-4.
9. Benkraouda M, Clem JR. Magnetic hysteresis from the geometrical barrier in type-II superconducting strips. Phys Rev B. 1996;53:5716.
10. Brandt E H, et al. Statics and dynamics of the flux-line lattice in realistic geometries. NATO ASI. 1999;356:81-108 .
11. Blatter G, Feigel'man M V, Geshkenbein V B, et. al. Vortices in high-temperature superconductors. Rev. Mod. Phys. 1994;66:1125.
12. Bean C. P, Livingston J D. Surface barrier in type-II superconductors. Phys. Rev. Lett. 1964;12:14.
13. Ruslan P. Static and dynamic irreversible magnetic properties of high temperature sperconductors 1998;113:173.