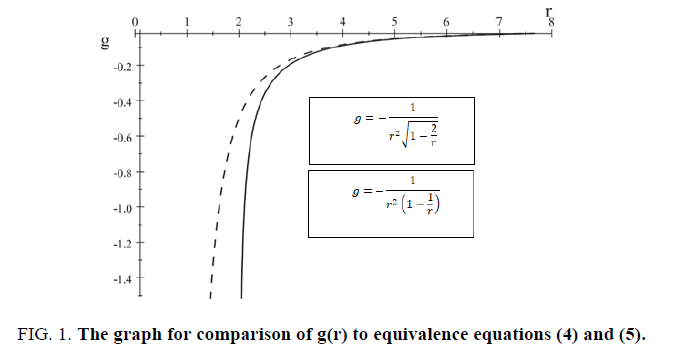Short communication

, Volume: 7( 1) DOI: 10.37532/2320-6756.2019.7(1).170

• View PDF
• Download PDF

Semi-Classical Solution to a Schwarzschild Problem Almost Entirely Congruent to the New Law of Gravity

*Correspondence:

Gobato R Laboratory of Biophysics and Molecular Modeling Genesis, State Secretariat of Education of Parana, Bela Vista do Paraiso, Parana, Brazil, E-Mail: ricardogobato@hotmail.com

Abstract

One of spherically symmetric solutions of field equation corresponds to Schwarzschild solution, while most part of its Christoffel symbols are asymptotically equal to Christoffel symbols of Schwarzschild’s metric tensor. In particular, the gravity field acceleration given by the new solution coincides with the gravity field acceleration given by the Schwarzschild solution in weak fields. For homogeneous space, the field equation returns the metric with exponential dependence on time, which is imposed by space. Einstein’s equation in the new version performs another function: it allows calculating the full tensor of energy-momentum of matter and field via a metric tensor. Namely the new solution with the spherical symmetry in space without matter is the field of “gravity” forces oriented outwards. In this case, a role of “dark energy” is played by the gravity field negative energy density. Sizes of this object are proportional to absolute value of field energy and not limited at all. It is assumed that namely such solutions are responsible for the large-scale structure of the Universe. Gravity field energy density was computed in the frame of the Newtonian gravity theory. The Newtonian gravity law was deduced with a correction for a non-zero density of a gravity field. The new gravity law is virtually almost entirely congruent with the Schwarzschild mutual attraction law in a zone somewhat distant from the Schwarzschild radius. The assumption was outspoken that the Einstein’s refusal from the energy of a gravitational field as a field source in the Einstein’s equation could result in noticeable errors in solutions of this equation.

Keywords

General Relativity Theory; Gravity field energy density; Newtonian gravity theory; Schwarzschild problem

Introduction

Newton's law has since been superseded by Albert Einstein's theory of general relativity, but it continues to be used as an excellent approximation of the effects of gravity in most applications. Relativity is required only when there is a need for extreme precision, or when dealing with very strong gravitational fields, such as those found near extremely massive and dense objects, or at very close distances (such as Mercury's orbit around the Sun) [1,2].

Any object whose radius is smaller than its Schwarzschild radius is called a black hole. The surface at the Schwarzschild radius acts as an event horizon in a non-rotating body (a rotating black hole operates slightly differently). Neither light nor particles can escape through this surface from the region inside, hence the name "black hole"[3].

Black holes can be classified based on their Schwarzschild radius, or equivalently, by their density. As the radius is linearly related to mass, while the enclosed volume corresponds to the third power of the radius, small black holes are therefore much denser than large ones. The volume enclosed in the event horizon of the most massive black holes has an average density lower than main sequence stars [3].

The Schwarzschild radius of a body is proportional to its mass and therefore to its volume, assuming that the body has a constant mass-density. In contrast, the physical radius of the body is proportional to the cube root of its volume. Therefore, as the body accumulates matter at a given fixed density (in this example, 103 kg/m3, the density of water), its Schwarzschild radius will increase more quickly than its physical radius. When a body of this density has grown to around 136 million solar masses (1.36 × 108) M☉, its physical radius would be overtaken by its Schwarzschild radius, and thus it would form a supermassive black hole [3].

A relativistic relation between energy and mass does not depend on energy nature, i.e. any energy type-whether it would be the energy of matter or energy of fields can be considered as mass. The principle of equivalence of inertial and gravitational masses makes necessary consideration of total energy in a specified volume as a source of a gravity field. Besides, the gravity field would have energy, if relying on the energy conservation law. Together with the other principles of the general relativity theory, this principle was put forward by A. Einstein in his famous paper [4]. Upon that, Einstein made the important notice:

“It can be seen that along with the components of the energy-tensions tensor of a matter T_ik as equivalent field sources, also components of a gravity field tensor (namely θ_ik) act. Evidently, this requirement is necessary as a gravitational action of a system cannot depend on the physical nature of energy being the field source” [4].

However, in the course of the search of his gravity field equation in the general relativity theory, Einstein was forced refusing from the energy of a gravity field as a gravity field source. In other words, in the right part of the equation now known as the Einstein’s equation, there is the matter energy-momentum tensor including an electromagnetic field but not including a gravitational mass.

It should seem, this fact would make everyone relating with cautiousness to the Einstein’s equation solutions. Nevertheless, curiously enough, this historical fact has been little known to a considerable part of professionals. Worthy of special mention is the notice by L.D. Landau and E.M. Lifshitz in the second volume of their manual (section 95 “Einstein’s Equations”) [5]:

“The gravitational interaction plays a role only for bodies with a big enough mass (due to the smallness of the gravitation constant). That is why in gravity field researches usually, we have a deal with macroscopic bodies”.

Now, the question on the limits to the applicability of the Einstein’s equation arouses extremely sensitive. That is why it is important to clarify the role of the energy of a gravity field as a source of the field itself.

Using solely the Newtonian gravity theory, let us consider a spherically symmetric problem of finding gravity field and compare it with the Schwarzschild solution.

Methodology

The classical energy density of a gravity field

Calculating the energy density of a gravity field in the Newtonian limit and considering a thin heavy spherical membrane of a mass M . The acceleration of free fall on the membrane surface is equal to

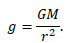(1)

Increase the radius by a small value 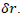Upon that, the membrane internal volume grew by the value 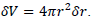Along with this, at the membrane radius growth, it is necessary to perform a work equal to 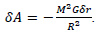From which the energy density of a gravity field is equal to

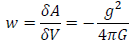
This value differs from the value obtained as the Newtonian limit in the general relativity theory [3].

The semi-classical gravity field of a point source

Evaluating the impact of an addition of mass density, the equivalent energy (3)-on a point mass Newtonian field is. In this problem apart from the central mass, the total mass includes an equivalent of the field mass. Then with due account of the correction factor (r) to the mass M, the Newtonian gravity law can be written as follows:

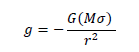(2)

Where m is a function of . The following value must be considered as the mass density

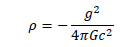(3)

This allows-based on (1)-evaluating an augment of a gravity field of a mass membrane having a radius r and a thickness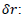

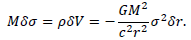
In the limit, have the differential equation

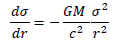
from where the correction factor σ can be found. As a result with the die account of the “weight” of the gravity field, the gravity law acquires the following form:

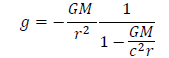(4)

This law 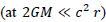coincides virtually with the well-known gravity law following from the Schwarzschild solution (FIG. 1):

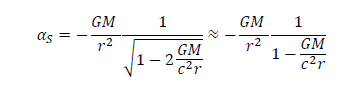(5)

Semi-classical solution and general relativity theory

Classifying the obtained solution as a random coincidence or just a curious fact is impossible. The connection becomes evident between Einstein’s postulate about the field energy as a field source on one hand and the solutions of the equation of the general relativity theory on the other hand. Now one should be surprised with that extremely successful application of the Einstein’s equation, notwithstanding that it contradicts to the Einstein’s postulate.

See a possible theory development way in the replacement of the Einstein’s equation with the other one [6] and in a development of cosmological models against the background of homogeneous space [6-20].

Discussions

Schwarzschild's solution

Schwarzschild's solution was obtained under Einstein's condition of emptiness: setting all the components of the Ricci tensor equal to zero.

How do you explain a central mass? If it is a mass you have only one in the universe. What is the gravitational attraction between?

In the words of Barrett O'Neill, the central mass M is "not to be modeled". (Bernard Howard Lavenda, Pisgat Shoresh, Apt 634 908600, O Shoresh, Israel, September 21, 2018.)

It is true, but the article solves the classical problem in the Newtonian approximation. Only Einstein's hypothesis about the equivalence of energy as a generator of the gravitational field is used [1]. The only element of the relativistic theory is the equality: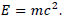

The solution

The solution to his differential equation is 1/sigma=-GM/r^2+ const. Where is this expression in his equation (4)? So why write down a d.e. if you don't use it?

The Equation (4) is the solution of the differential equation

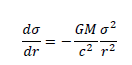
If there are difficulties with the symbol δ it can be replaced by d.

Einstein's equivalence principle

Einstein's equivalence principle is less than a principle. Where is the equivalency between angular acceleration and a gravitational field?

“I did not mean Einstein's "equivalence principle". Only the equivalence of mass and energy. The word "principle" can be removed from the text. This will make the text more understandable (FIG. 2).

Relativistic jet, which, probably, is accelerated by gravity field and dispersed on the gas-dust cloud. (This Hubble Space Telescope photograph shows the jet of matter ejected from M87 at nearly the speed of light, as it stretches 1.5 kpc (5 kly) from the galactic core) [6,21].

Conclusions

This was not a general relativity check. Understand how true Einstein's hypothesis is about the equality of all types of energy as sources of the gravitational field. The result was unexpected. The gravitational field in the Newtonian limit almost coincided with the Schwarzschild solution.

This suggests that the Einstein hypothesis could lead to a more accurate equation of the gravitational field. The program Implemented by Einstein failed. In the modern general covariant equation of Einstein does not contain the energy of the gravitational field in the right-hand side. The more surprising is the success of the Einstein equation in solving gravitational problems.

Based on what has been said it can assume that the development of general relativity can go along the path of abandoning the Einstein equation. Some progress has already been made in this direction.

Acknowledgments

Prof. Ph.D. Bernard Howard Lavenda, for questioning.

References

1. Creative C. Newton's law of universal gravitation. 2018.
2. Newton I. "In [experimental] philosophy particular propositions are inferred from the phenomena and afterward rendered general by induction: Principia", General Scholium. Motte's English translation. 1729;2:392.
3. Schwarzschild radius. 2018.
4. Einstein A, Grossmann M. Entwurf einer verallgemeinerten Relativitätstheorie und Theorie der Gravitation. Z Mat, und Phys. 1913;62:225-61.
5. Landau LD, Lifshitz EM. The Classical Theory of Fields. Pergamon Press, Oxford. 1975.
6. Morozov VB. New version of the general theory of relativity (Initial principles. New gravitational field equation. New solutions. 2018.
7. Morozov VB. Homogeneous empty space density is built of dark energy plus dark matter. ResearchGate. 2018.
8. Kuzmichova VA, Morozov VB. Semi-classical solution of Schwarzschild problem. ResearchGate 2018.
9. Faddeev LD. The energy problem in Einstein’s theory of gravitation” (Dedicated to the memory of V.A. Fock). Sov Phys Usp. 1982;25:130-42.
10. Denisov VI, Solov'ev VO. The energy determined in general relativity on the basis of the traditional Hamiltonian approach does not have physical meaning. Theoretical and Mathematical Physics. 1983;56:832-84.
11. Vizgin VP, Smorodinskii Y. A From the equivalence principle to the equations of gravitation. Sov Phys Usp. 1979;22:489-513.
12. Einstein A. Die Bemerkung zu Schrödingers Notiz über das Lojsungssystem der allgemein kovarianten Gravitationsgleichungen. Phys Z. 1918;19:165-6.
13. Zeldovich YAB. Is the formation of the universe “out of nothing” possible? Nature. 1988;2.
14. Chernin AD. Dark energy and universal antigravitation. Phys Usp. 2008;51:253-82.
15. Morozov VB. Gravity field equations. Expulsive solution. Dark energy. ResearchGate. 2016.
16. Streltsov VN. The energy-momentum tensor of the gravitational field. Reports of the Joint Institute for Nuclear Research. ResearchGate. 2016.
17. Einstein A. Approximately integration of the field equations of gravity, Sitzungsber Preuss Akad Wiss. 1916;1:688-96.
18. Einstein A. The remark on Schrodinger's note on the Lojs system of the generally covariant equations of gravitation. Schrödingers Phys Z. 1918;19:20.
19. Morozov VB. Einstein’s Equation. Parana J Sc. Educ. 2018;46-9.
20. Einstein A, Fokker AD. Nordstrom's theory of gravitation from the point of view of absolute differential calculus. Ann Phys. 1914;44:321-8.
21. http://hubblesite.org/image/968/category/4-galaxies.