Original Article
, Volume: 5( 4)Relationships Between Two Gravitationally-Bound Points in Single or Multiple Systems In The Universe
- *Correspondence:
- Jihai Zhang Sr.Electrinics Designer, Canada, Tel: 613-721-2937; E-mail: z.jihai@gmx.com
Received Date: June 29, 2017 Accepted Date: July 20, 2017 Published Date: August 06, 2017
Citation: Zhang J and Tao P2. Relationships Between Two Gravitationally-Bound Points in Single or Multiple Systems In The Universe. J Phys Astron. 2017;5(2):116.
Abstract
Supported by real data, this article derives and proves relationships for any two gravitationally-bound objects in single or multiple systems in the universe. These findings have implications for simpler and more accurate calculations in related practical applications [1][2]. Normally, relative error is less than 3.35%.
Keywords
Gravity; Centrifugul force; N body; Gravitational field; Solar system; Exoplanet; Universe
Introduction
Gravitationally-bound objects that orbit a central object (single system) or different central objects (multiple systems) are general phenomena in the universe. It is therefore very meaningful to find the relationships between two gravitationally-bound points in single or multiple systems in the universe.
In this article, the case of the common centre is first discussed (single system examples: planets orbiting the Sun, moons orbiting a planet) and then, the second case of multiple centres with different central masses is discussed (multiple system examples: different moons orbiting different planets).
In these two systems, results show that the relationship between gravity and centrifugal force is the same, however, the relationships between any two gravitationally-bound points are different but convertible, and normally, the maximum relative error is less than 3.35%.
Derivation and Verification
Relationships between two points around the same centre (single system):
Centrifugal force:  (1)
(1)
then  (1b)
(1b)
Where, m is the mass of an orbiting body.
Gravitation:  (2)
(2)
Then 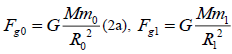 (2b)
(2b)
Where, M is the mass of the centre.
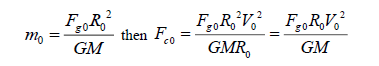 (3)
(3)
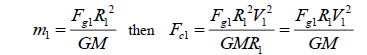 (4)
(4)
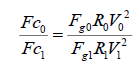 (5)
(5)
When 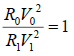 (6)
(6)
Or 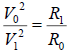 (7)
(7)
Then 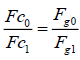 (8)
(8)
Following are verifications of equation (7) : 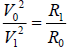 using real data.
using real data.
Verifications between the 8 planets in the Solar System as orbiting satellites and the Sun as the common centre.
Where absolute error 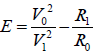 (9)
(9)
Relative error 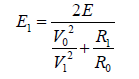 (10)
(10)
Table 1, Table 2 and Table 3 show that E1max is less than 2.11%, due to the source data being averages. The results proved
equation (7): 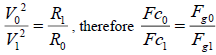 (8).
(8).
| Planet | V0 (km/s) |
R0 (km) |
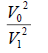 |
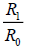 |
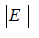 |
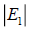 |
|---|---|---|---|---|---|---|
| Neptune | 5.43 | 4495.06 | 0.033246832 | 0.03328098 | 3.41473E-05 | 0.001026557 |
| Uranus | 6.8 | 2872.46 | 0.052139689 | 0.052080795 | 5.88944E-05 | 0.001130189 |
| Saturn | 9.68 | 1433.53 | 0.105657743 | 0.104357774 | 0.001299968 | 0.012379737 |
| Jupiter | 13.06 | 778.57 | 0.192325543 | 0.192147142 | 0.000178401 | 0.000928031 |
| Mars | 24.07 | 227.92 | 0.653285161 | 0.656370656 | 0.003085495 | 0.004711918 |
| Venus | 35.02 | 108.21 | 1.382874908 | 1.382496997 | 0.000377791 | 0.000273317 |
| Mercury | 47.36 | 57.91 | 2.529146582 | 2.583318943 | 0.054172361 | 0.021192264 |
Verifications between Jupiter’s 4 moons.
Table 1. Where V1 and R1 are Earth’s data, V1= 29.78 (km/s), R1=149598023 (km). Note: V1 and R1 can be data from any of the 8 planets (verified and confirmed) [3].
| Moon of Jupiter | V0 (km/s) |
R0 (km) |
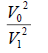 |
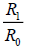 |
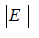 |
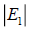 |
|---|---|---|---|---|---|---|
| Europa [5] | 13.74 | 670900 | 0.628312762 | 0.628558652 | 0.000245891 | 0.000391274 |
| Ganymede [6] | 10.88 | 1070400 | 0.393967327 | 0.393964872 | 2.45406E-06 | 6.2291E-06 |
| Callisto [7] | 8.204 | 1882700 | 0.22400294 | 0.223986827 | 1.61126E-05 | 7.19328E-05 |
Verifications between Saturn’s 4 moons.
Table 2. Verifications between Jupiter’s 4 moons. Where V1 and R1 are moon Io’s data, V1= 17.334 (km/s) [4], R1=421700 (km) [4]. Note: V1 and R1 can be data from any of the 4 moons (verified and confirmed).
| Moon of Saturn | V0 (km/s) |
R0 (km) |
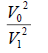 |
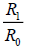 |
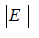 |
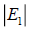 |
|---|---|---|---|---|---|---|
| Tethys [9] | 11.35 | 294619 | 0.631735537 | 0.629759112 | 0.001976273 | 0.003133465 |
| Rhea [10] | 8.48 | 527108 | 0.352643018 | 0.351994278 | 0.00064874 | 0.001841344 |
| Titan [11] | 5.57 | 1221870 | 0.1521437 | 0.151848396 | 0.000295304 | 0.001942842 |
Table 3. Verifications between Saturn’s 4 moons. Where V1 and R1 are moon Mimas’ data, V1= 14.28 (km/s) [8], R1=185539 (km) [8]. Note: V1 and R1 can be data from any of the 4 moons (verified and confirmed).
Relationship Between Two Points Around the Different Centres (Multiple Systems):
There are two kinds of relationships in a multiple system, one is the relationship between any two points around the same centre (single system) and another is the relationship between any two points around different centres (multiple systems). The following discusses relationships found in multiple systems, however the formerly discussed single system relationships are still valid and applied [4-10].
According to equation (3), 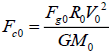 (11)
(11)
Where M0 is the central mass of single system A, R0 is the distance from the orbiting point 0 to the centre.
According to equation (4), 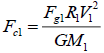 (12)
(12)
Where M1 is the central mass of single system B, R1 is the distance from the orbiting point 1 to the centre.
Then 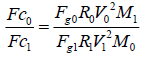 (13)
(13)
When 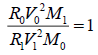 (14)
(14)
Then 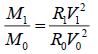 (15)
(15)
When 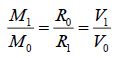 (16)
(16)
Then 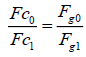 (17)
(17)
Following are Verifications Of Equation (16) :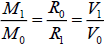 Using Real Data( V0 And R0 are Theoretical Data).
Using Real Data( V0 And R0 are Theoretical Data).
Example of detailed calculations between Jupiter’s moon Io and Saturn’s moon Mimas:
Where M1, V1 and R1 are Jupiter’s data and M0, V0 and Vx and Rx are Saturn’s data, V0 and R0 are Saturn’s theoretical data obtained from real data.
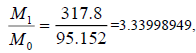 R1=421700(km)(moon Io)[9], according to equation( 16):
R1=421700(km)(moon Io)[9], according to equation( 16):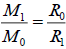
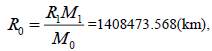
Vx=14.28(km/s)[13], Rx=85539(km)( moon Mimas)[13], according to equation( 7): 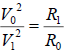
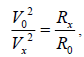 then
then
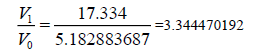
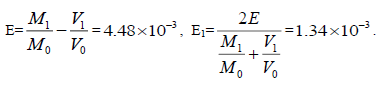
Table 4 shows that E1max is 0.00488. The results proved equation (16): 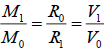
and therefore, equation (8): 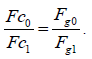
| Moons | M0 | Vx (km/s) | Rx (km) | R0 (k [m) | V0 (km/s) | 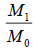 |
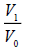 |
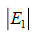 |
|---|---|---|---|---|---|---|---|---|
| Mimas [8] | 95.152 [3] | 14.28 | 185539 | 1408473.568 | 5.18288 | 3.34 | 3.344 | 0.00134 |
| Miranda [14] | 14.536 [3] | 6.66 | 129390 | 9219610.622 | 0.78898 | 21.86 | 21.97 | 0.00488 |
| Phobos [12] | 0.107 [3] | 2.138 | 9376 | 1252488411 | 0.00585 | 2970 | 2963 | 0.00231 |
| Moon [13] | 1 [3] | 1.022 | 384399 | 134016260 | 0.05473 | 317.8 | 316.7 | 0.0035 |
Table 4. Verifications between Jupiter’s moon Io, Saturn’s moon Mimas, Uranus’ moon Miranda, Mars’ moon Phobos and Earth’s moon. These moons orbit different centres with different central masses (this multiple system consists of 5 single systems). Note: Although M1, V1 and R1 are Jupiter’s data (M1=317.8 [3], V1=17.334 (km/s) [4] and R1=421700 (km) [4]), these data can be from any of the 5 single systems (verified and confirmed).
Conclusion
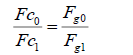 (8)
(8)
Where, Fc0 and Fc1 are centrifugal forces of any two points around the same or different centres, Fg0 and Fg1 are gravitational forces with distances of R0 and R1 to the corresponding centres.
Relationship between two points around the same centre (single system):
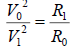 (7
(7
Where, V0 and V1 are cross-radial velocities with distances of R0 and R1 to the centre respectively [Tables 5-7].
| Moons | M0[3] | V0(km/s) | R0(km) | k | Average k |
|---|---|---|---|---|---|
| Mimas[8] | 95.152 | 14.28 | 185539 | 2.51493E-06 | 2.50863E-06 |
| Miranda[14] | 14.536 | 6.66 | 129390 | 2.53277E-06 | |
| Phobos[12] | 0.107 | 2.138 | 9376 | 2.49661E-06 | |
| Moon[13] | 1 | 1.022 | 384399 | 2.49067E-06 | |
| Io[4] | 317.8 | 17.334 | 421700 | 2.50815E-06 |
Table. 5. calculations of constant k based on the data of the 5 planets and their moons
| Planet[3] | V0(km/s) | R0(k[m) | k | MSUN | E1 |
|---|---|---|---|---|---|
| Neptune | 5.43 | 4.50E+09 | 2.51E-06 | 3.32E+05 | -0.001547221 |
| Uranus | 6.81 | 2.87E+09 | 2.51E-06 | 3.34E+05 | 0.003553643 |
| Saturn | 9.69 | 1.43E+09 | 2.51E-06 | 3.38E+05 | 0.014020461 |
| Jupiter | 13.07 | 7.79E+08 | 2.51E-06 | 3.34E+05 | 0.001938855 |
| Mars | 24.13 | 2.28E+08 | 2.51E-06 | 3.33E+05 | -0.0002545 |
| Venus | 35.02 | 1.08E+08 | 2.51E-06 | 3.33E+05 | -0.000248513 |
| Mercury | 47.87 | 5.79E+07 | 2.51E-06 | 3.33E+05 | -0.000292851 |
| Earth | 29.78 | 149598023 | 2.51E-06 | 3.33E+05 | -0.000534934 |
Table. 6. verification results of equation (17): 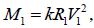 to calculate the mass of the Sum and error E1 based on the data of the 8 planets and the Sun(M=333000[3]) to confirm k=2.50863E-6.
to calculate the mass of the Sum and error E1 based on the data of the 8 planets and the Sun(M=333000[3]) to confirm k=2.50863E-6.
| Exoplanet | R(AU) | T(day) | M | M1 | E1 |
|---|---|---|---|---|---|
| Centauri[15][16] | 0.0485 | 11.186 | 0.12121 | 0.121612946 | 0.003318847 |
| PSR B1257 | 0.19 | 25.262 | 1.4 | 1.433605191 | 0.023719035 |
| [17][18][19][20] | 0.36 | 66.5419 | 1.4 | 1.405469195 | 0.003898952 |
| 0.46 | 98.2114 | 1.4 | 1.346027444 | -0.039309553 | |
| Gliese436[21][22] | 0.0291 | 2.6339 | 0.46 | 0.473788621 | 0.029532638 |
Table. 7. verification results of equation (17) using exoplanet data( R, T and M), M is real central star mass, M1 is calculation central star mass, E1 is Error( max: 3.9%, average: 1.28% ).
Relationship between two points around the different centres (multiple systems):
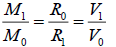 (16)
(16)
Where, M0 and M1 are corresponding central masses, V0 and V1 are cross-radial velocities with distances of R0 and R1 to the centres respectively.
Gravitationally-bound point in single or multiple systems in the universe:
According to (15): 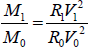
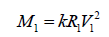 (17)
(17)
where 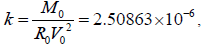 unit of M1 is Earth mass
unit of M1 is Earth mass
Where, V0 and V1 are cross-radial velocities with distances of R0 and R0 to the centre respectively.
Explanation
This article finds and establishes the theoretical/ideal relationships between two gravitationally-bound points in single or multiple systems in the universe, and uses real data to verify the calculation errors (the real statistic impact of the N body issue[1][2], N = 9, 8 planets + Sun) in these relationships. Especially, Equations (7),(16) and (17) are independence in gravity and centrifugal force, (17) is verified and confirmed by real data from both local and exoplanets.
Normally, when the orbit of a gravitationally-bound point approximates a circle, the theoretical/ideal relationships between two gravitationally-bound points can be expressed by equations (7), (8),(16) and (17) with about 3.35% error ( average: 0.6%). The N body issue exists, however, its impact is limited / even negligible.
Equation (8) represents the relationship between gravity and centrifugal force. According to equation (8), gravity and centrifugal force change in the same direction at the same ratio [11-22].
Equation (17) represents the relationship between gravitationally-bound point and central mass. According to equation (17), once we know any two of the factors: cross-radial velocity V1, the central mass M1 or the distance R1, we can calculate the corresponding distance R1 or central mass M1 or cross-radial velocity V1 of a moon, a planet or a star.
Given that k is an universal constant. Now we can use equations (17) to explain why there are many exoplanets orbit their central stars at very high speed V in a very short distance R.
In summary, these findings are properties of gravitational field, prove physical laws are universal and can be used to accurately identify exoplanets.
References
- https://en.wikipedia.org/wiki/N-body_problem
- https://en.wikibooks.org/wiki/Astrodynamics/N-Body_Problem
- https://nssdc.gsfc.nasa.gov/planetary/factsheet/
- https://en.wikipedia.org/wiki/Io_%28moon%29
- https://en.wikipedia.org/wiki/Europa_%28moon%29
- https://en.wikipedia.org/wiki/Ganymede_%28moon%29
- https://en.wikipedia.org/wiki/Callisto_%28moon%29
- https://en.wikipedia.org/wiki/Mimas_%28moon%29
- https://en.wikipedia.org/wiki/Tethys_%28moon%29
- https://en.wikipedia.org/wiki/Rhea_%28moon%29
- https://en.wikipedia.org/wiki/Titan_%28moon%29
- https://en.wikipedia.org/wiki/Phobos_%28moon%29
- https://en.wikipedia.org/wiki/Moon
- https://en.wikipedia.org/wiki/Miranda_%28moon%29
- https://en.wikipedia.org/wiki/Proxima_Centauri
- https://en.wikipedia.org/wiki/Proxima_Centauri_b
- https://en.wikipedia.org/wiki/PSR_B1257%2B12
- https://en.wikipedia.org/wiki/PSR_B1257%2B12_A
- https://en.wikipedia.org/wiki/PSR_B1257%2B12_B
- https://en.wikipedia.org/wiki/PSR_B1257%2B12_C
- https://en.wikipedia.org/wiki/Gliese_436
- https://en.wikipedia.org/wiki/Gliese_436_b

