Research
, Volume: 13( 2) DOI: 10.37532/2320-6756.2025.13(2).405QCD's Low-Energy Footprint
Rami Rom*
Department of Atomic Energy, Theoretical and Computational Physics Section (TCPS), Raja Ramanna Centre for Advanced Technology (RRCAT), Madhya Pradesh, India
- *Correspondence:
- Rami Rom
Department of Atomic Energy, Theoretical and Computational Physics Section (TCPS), Raja Ramanna Centre for Advanced Technology (RRCAT), Madhya Pradesh, India
E-mail: romrami@gmail.com
Received: April 10, 2024, Manuscript No. TSPA-24-132022;Editor assigned: April 15, 2024, PreQC No. TSPA-24-132022 (PQ); Reviewed: April 29, 2024, QC No. TSPA-24-132022;Revised: March 07, 2025, Manuscript No. TSPA-24-132022 (R); Published: March 14, 2025, DOI. 10.37532/2320-6756.2025.13(2).405.
Citation: Rom R. QCD’s Low-Energy Footprint. J Phys Astron. 2025; 13(2). 405.
Abstract
QCD affects electrons, nucleons and gravity through the vacuum quark and gluon condensate dynamics. We propose a model for electron motion by quark and antiquark flavor exchange waves in a pion tetrahedron lattice that represents the non-empty vacuum and estimate the quark flavor exchange wave energy density for the hydrogen atom. The magnetoresistance and spin torque of ferromagnetic layers may be explained by the proposed electrons and pion tetrahedron gas model. We suggest adding the pion tetrahedrons condensate energy density to Einstein’s equation energy-momentum tensor. QCD has a significant low-energy footprint and the quark flavor exchange wave may be an interesting example for the way QCD affects the dynamics of electrons.
Keywords
Quantum chromodynamics; Quantum electrodynamics; Electron-ion collider; Pion tetrahedrons; QCD vacuum; Spin waves; Magnetic materials; Magnetic tunnel junction; General relativity; Energy-momentum tensor; Friedmann equation
Introduction
The electron and pion tetrahedron clouds
The Electron-Ion Collider (EIC) is aimed to explore the building blocks of matter and reveal the properties of the strong force that binds the protons and neutrons together to form the nuclei [1]. The EIC is aimed to explore the three-dimensional distributions in coordinate and momentum spaces of the quarks and gluons and the way in which the nucleons mass, spin and mechanical properties emerge from the fundamental interactions of the quarks and gluons. The EIC program will include exotic meson spectroscopy aimed to observe the exotic meson states.
In this paper we argue that QCD has a low-energy footprint that affects electrons, atoms and gravity through the quark and gluon condensate dynamics. In previous papers [2-4] the exotic meson, uddu pion tetrahedron and the electron tetrahedron models were presented. We assumed that the exotic meson pion tetrahedron, uddu fill space and form a non-uniform condensate with an atmospheric like density drop. The pion tetrahedron mass may be calculated by measuring the β decay rate time periodic variability [3]. We further assumed that the attraction between quarks and antiquarks may be the source of gravity [2]. The massive pion tetrahedrons density vary according to the gravitational field in space and the gravitational force is transferred by interaction of quarks with the anti-quarks of the non-uniform pion tetrahedron condensate.
We further assumed that the electron may be a comprised particle, a tetra quark tetrahedron, two quarks determine its electric charge and two quarks determine the electron spin. High frequency quark exchange reactions may transform the electron tetrahedrons to pion tetrahedrons and vice versa and form together electron clouds with fixed spin state [2]. The uu and uu quark pairs assumed to be part of the electron tetrahedrons, allow forming chemical bonds between electron pairs and proton-neutron pairs in the nuclei forming the uddu pion tetrahedron that act as a QCD glue. We assumed that the valence quarks and antiquarks (u, d, d and u are conserved sub-particles and may only be exchanged between reactants forming products.
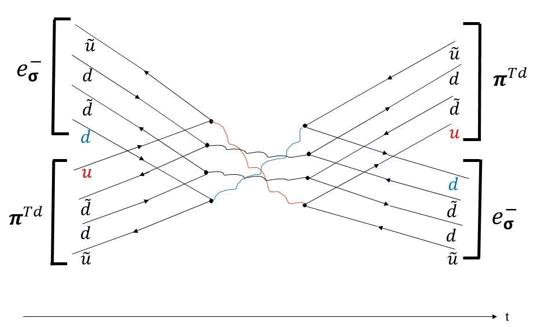
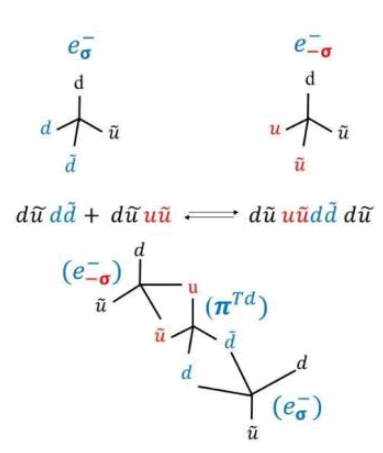
In this paper we propose that electron and pion tetrahedrons form together electron clouds in thermal equilibrium due to high frequency quark exchange reactions that occur between the electrons and the pion tetrahedrons forming a quark and antiquark flavor exchange waves. We further assume that two electron tetrahedrons scattering having opposite spins create a pion tetrahedron transition state complex that act like a QCD glue and dissipate heat to the pion tetrahedron condensate generating an electric resistance (Figure 1).
FIG. 1. Illustrates an electron tetrahedron and pion tetrahedron scattering exchanging d and u quarks, transforming the electron to a pion tetrahedron and vice versa. High frequency repetition of the quark exchange reactions generate an electron cloud that conserves charge and spin and may be seen as a quark flavor exchange wave.
We assume that when an electron is accelerated a plurality of pion tetrahedrons that surround it are accelerated with the electron in thermal equilibrium due to the rapid quark exchange reactions. The electron cannot be separated from its surrounding pion tetrahedrons cloud and the electron becomes a many-body cloud composed of a plurality of pion tetrahedrons that perform rapid d and u quark exchange reactions with the electron tetrahedron. The thermal equilibrium with the pion tetrahedron condensate assumption applies not only to electrons. Protons and neutrons participate also in the rapid quark exchange reactions with the vacuum pion tetrahedrons. We assume that protons and neutrons of atom nuclei in a solid state are surrounded by the vacuum pion tetrahedrons since the pion tetrahedrons antiquarks are attracted to the quarks of the protons and neutrons. Since the density of matter inside the solid is much higher than in a gas, the non-uniform pion tetrahedron condensate density inside a solid may be higher and may also follow the lattice symmetry. In the next sections we describe the electron and pion tetrahedrons motion in a lattice in a hydrogen atom model generating quark flavor exchange waves.
Electron and pion tetrahedron cloud and the hydrogen atom
Werner Heisenberg introduced in 1925 matrix mechanics trying to explain the electron trajectories (x(t), p(t)) for the hydrogen atom in an electromagnetic field arguing that the electrons do not move in classical orbits as Niels Bohr suggested [5]. Quantum mechanics explained electron dynamics in terms of wave functions and discrete energy levels according to equations that were derived a year later by Erwin Schrodinger and in 1928 by Paul Dirac. The wave mechanics gave the correct spectra and the probability to find the electron but it did not provide a detailed description of the electron motion in classical trajectories or in another pattern.
The hydrogen atom hyperfine structure Hamiltonian may be written in terms of Dirac’s exchange operator pex, the exchange energy parameter A and the Pauli spin matrices for the electron ?? and the proton ?? are
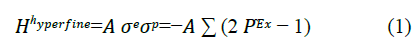
Dirac’s exchange operators pex, exchanges the two particles’ spins. If their spins are in the same state the overall spin state remains unchanged but if their spin states are anti-parallel the two spins are switched.
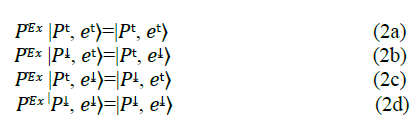
The hyperfine Hamiltonian matrix in the basis set of the four possible spin states, |pt, et |pt, et |pt, et |pt, et | is given by the following 4 × 4 matrix [6].
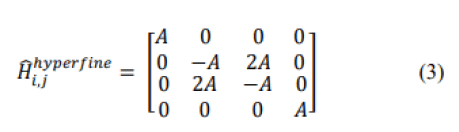
Solving the time dependent Schrodinger equation for the hyperfine Hamiltonian
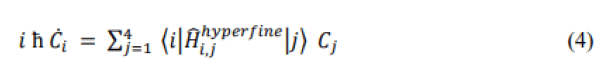
gives the ground state solution as an antisymmetric combination of the two anti-parallel spin states 1/√2 (|pt, et − |pt, et), with the ground state energy -3A and the three other states have the same positive energy +A. The total energy difference is ΔEhyperfine=4A. The hyperfine energy split is the source for the 21 cm line emission by hydrogen atom clouds in space of 5.87 10−6 eV. The hyperfine energy split is six orders of magnitude smaller than the difference between the hydrogen electronic ground state En=1hydrogen and its first excited states, En=2hydrogen, which is 10.2 eV. Dirac’s spin exchange operator PEx are used also in spinlattice models to exchange spins of two adjacent lattice sites generating spin waves with energies hwk=2A(1−cos(kb)), where for small k values, kb<<1 equals to hwk=Ak2b2 and an effective mass may be calculated.
The two aspects, i.e., the hyperfine energy split and spin waves are adapted below for the description of the hydrogen atom surrounded by a pion tetrahedrons lattice. We propose that the electron dynamics may be explained by rapid quark exchange reactions that occur between the electrons and the pion tetrahedrons we describe as quark and antiquark flavor exchange waves in analogy to spin waves. Accordingly, QCD affects the electron motion in atoms via the vacuum pion tetrahedron condensate.
We assumed in a previous paper that the electron tetrahedrons have two quark compositions that determine their spin state [7]. One electron tetrahedron has the quark composition du dd (spin up configuration) and the second electron tetrahedron quark composition is du uu (spin down configuration). The two electron tetrahedrons are surrounded by the vacuum pion tetrahedrons ? ?? ? forming together electrons clouds in thermal equilibrium. The exchanged quarks for the spin up electrons are the d and u quarks, while the exchanged quarks for the spin down electrons are the u and d quarks.
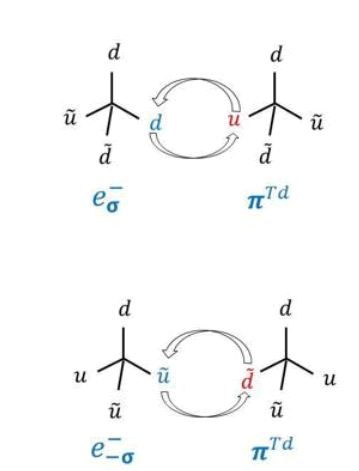
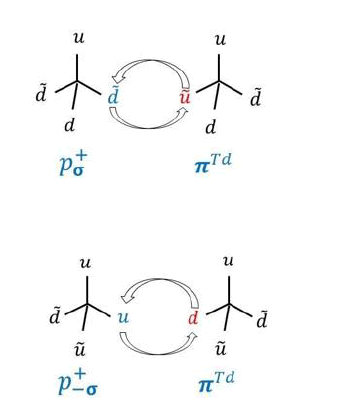
We adapt the spin lattice model for the QCD vacuum and assume that each lattice site contains a pion tetrahedron or an electron tetrahedron. The transition between the two occurs by exchanging a u quark with a d quark or a d and a d quarks as shown in Figure 2 below. Similar quark exchange reactions can be illustrated for spin up and spin down positrons exchanging d and u quarks or u and d anti-quarks as shown in Figure 3.
FIG. 2. Illustrates quark exchange reactions for the spin up and the spin down electrons with pion tetrahedrons. The exchanged quarks for the spin up electron are the d and u quarks, while the exchanged quarks for the spin down electron are the ? and the ? anti-quarks.
FIG. 3. Illustrates quark exchange reactions for the spin up and the spin down positrons with pion tetrahedrons.
The quark flavor exchange reactions may occur in two neighboring lattice sites and can also occur between two distant lattice sites, i and j, with a probability pi,j.
For the hydrogen atom model, we propose a pion tetrahedron lattice with two co-centric spheres. In each lattice site there is a pion tetrahedron |eij=|u d uu except for one site that contains an electron tetrahedron that we assume may have two possible configurations, a spin up electron configuration |πitd=|uddd|j or a spin down electron configuration |eij? = |uduu|.
Four states characterized by the underlying quark flavor exchange waves in the two co-centric spheres may exist according to which quarks are exchanged, the quarks or the anti-quarks in each sphere domain.
The two quark flavor exchange reactions are
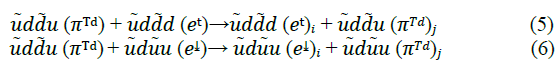
Where in the first quark flavor exchange reaction the u and d quarks are exchanged (equation 5) and in the second the ? and ? were exchanged (equation 6). The four states possible are:
(u, d) flavor exchange in the inner sphere and (u, d) flavor exchange in the outer sphere,
(u, d) flavor exchange in the inner sphere and (u d) flavor exchange in the outer sphere,
(u d) flavor exchange in the inner sphere and (u, d) flavor exchange in the outer sphere and
(u d) flavor exchange in the inner sphere and (u d) flavor exchange in the outer sphere.
In each of the quark flavor exchange reaction, the electron spin is conserved as equation 5 and 6 show. Interaction with the proton spin may flip the electron spin according to equation 7 below that we assume may occur on the surface between the two spheres for the electron. For the proton, the spin flip requires the exchange of a u u meson with a u u meson or vice versa.
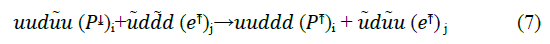
We note that the valence quarks and anti-quarks numbers are conserved by equation 7 and also that the proton’s mass is higher than the mass of its three valence quarks, uud, where the extra mass is typically explained by additional gluons and possibly virtual mesons. The nucleons structure and spin are main research topics of the EIC. We assume here that the proton contains additional u u or d d mesons that determine the proton spin states
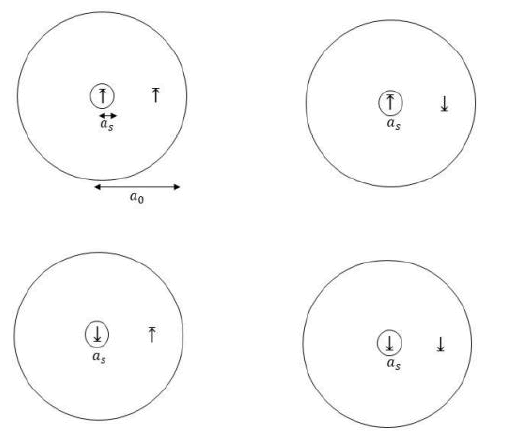
After the two spins are flipped, the quark flavor exchange wave can continue propagating according to equation 5 or 6 above in each domain. We assume that if the proton and electron spins are anti-parallel, the electron crosses the sphere surface smoothly with no need for a spin flip that cost in additional energy. The anti-parallel spin states are favorable and have lower energy. The four possible states of the two domains are shown below in Figure 4. The first domain is the inner sphere with a radius as and the second domain is the outer sphere with Bohr radius a0. If the proton and electron spins are antiparallel there is a single domain with the Bohr radius a0 for the quark flavor exchange waves.
FIG. 4. Illustrates the hydrogen atom model with two co-centric pion tetrahedron spheres where the quark flavor exchange waves occur in separated domains or a single domain.
With the proposed model, the hyperfine energy split may be explained by the quark flavor exchange wave domains. With anti-parallel spins, there is only one domain with a larger volume for the quark or antiquark flavor exchange waves. If the two spins are parallel, two separated quark flavor exchange wave domains are created and the configuration has higher energy.
We can estimate the radius of the internal domain sphere, ud, using the measured hydrogen atom hyperfine energy split of 5.87 10−6 eV and then calculate the quark flavor exchange wave energy density pE for the hydrogen atom electron and piontetrahedron cloud lattice model.
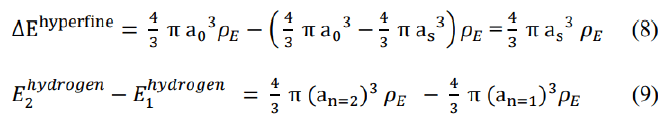
The ratio of the hyperfine energy and the difference between the hydrogen ground state (n=1) and the first excited states (n=2) is independent of the energy density pE and allows calculating the internal sphere radius as.
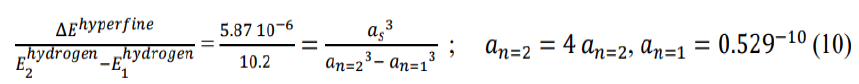
Accordingly, the radius of the inner domain, as, is 6.346−13 m and the ratio of as and Bohr radius is
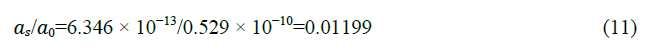
Next, we can calculate the quark flavor exchange wave energy density pE for the ground state of the hydrogen atom electron and pion tetrahedron cloud lattice using equation 8.
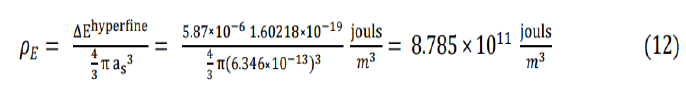
The quark flavor exchange wave energy density pE in eV per atom is

The quark flavor exchange wave energy density per atom, 3.4 eV, contributes about 25% of the hydrogen atom ground state energy of -13.6 eV. If we add the electron rest mass and the internal rotations and vibrations energy of the four pion tetrahedrons quarks in each lattice site as an effective rest mass energy, we may recover another 25% and over all get 50% of the ground state energy as a sum of kinetic and rest mass energies. The remaining 50% of the total ground state energy may be due to the electrostatic Coulomb potential of the proton.
In terms of the relativistic energy-momentum equation
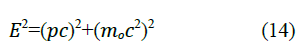
We can relate the kinetic energy term pc to the quark flavor exchange wave describing the hoping of an electron from site to site on the lattice and the second rest mass term moc2 with the electron rest mass and the internal rotation and vibration energies ineach site of the lattice. It should be noted that the proposed vacuum pion tetrahedron lattice cell length may be observed as contracted to a moving electron with a velocity v according to the Lorentz transformation.
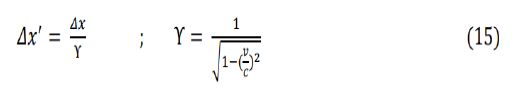
The motion of an electron in the vacuum pion tetrahedron lattice may be constrained to conserve the special relativity symmetry and we note that since the proposed pion tetrahedron lattice includes in each site a pion tetrahedron boson, uddu, excitations of the lattice may be constrained to have a left or right rotation of the electric field based on the internal motion of the quark charges (u−q) and du(+q) in each lattice site. The motion of massless excitation that may model photons may be further constrained to conserve the special relativity symmetry on the lattice.
The hydrogen atom hyperfine energy split is extremely small, 5.87 × 10−6 eV, however, in ferromagnets due to the long-range magnetic interaction and the heavy metals un-paired electrons, the spin-spin interaction becomes significant. In the next section the magnetoresistance of the electrons and pion tetrahedrons in a gas model is described.
The electron and pion tetrahedron gas resistance
In contrast to most electronic devices and circuits where the electric charge is the main player, magnetic materials use the electron spin to store data and the spin-orbit coupling to switch between the spin states. For example, hard drive discs use magnetic domains formed by typically 10 nanometer size ferromagnetic Co-Pt-Cr grains to maintain stable spin states logical level 0s and 1s. Magnetic read heads include typically two ferromagnetic layers, one with a fixed magnetization and a second with a varying magnetization sensitive to the magnetic domains maintained by hard drive discs. The current that flows through the magnetic read head depends on the spin alignment of two ferromagnetic layers that produce the Giant Magnetic Response (GMR) discovered by Fert and Grünberg [8].
Sinova et al. described the spin hall effect and Mott’s double scattering spin polarization proposed in 1929 inspired by Dirac’s electron theory and Magnetic Tunnel Junctions (MTJ) [9-11]. First scattering of an electron beam on heavy atom target creates a spin polarized beam that is scattered again by a second heavy atom target creating two currents that can be measured with different chirality.
We propose the following electron and pion tetrahedron gas resistance model that may be used to explains MTJs and Mott’s double scattering. We assume that scattering of two electron tetrahedrons with the same spin that share their pion tetrahedron clouds are elastic collisions with no quark exchange and heat dissipation.
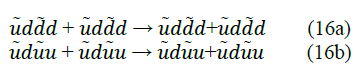
However, the scattering of two opposite spin electron tetrahedrons occurs via a pion tetrahedron transition state complex (uddduuudt, equation 17a) and is an inelastic reaction between the two electron tetrahedrons where quarks are exchanged, heat is dissipated to the pion tetrahedron condensate causing a friction for the electric current flow and switching the electrons’ spin as shown in equation 17b (the d d and uu are exchanged).
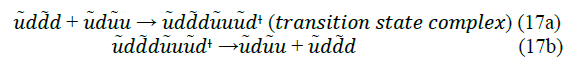
Note that both d and d quarks are exchanged with u and u quarks of the second electron.
The quark exchange reaction via the pion tetrahedron transition state complex cause heat dissipation and electrical resistance that is explained typically by scattering of electrons on solid impurities and the nuclei motion (solid-state phonons). The electron and pion tetrahedron gas model resistance may be an additional spin dependent mechanism. The proposed quark flavor exchange wave model includes a possible spin-spin interaction between electrons and protons (equation 7 above) that may be equivalent to electrons interactions with the solid-state phonons.
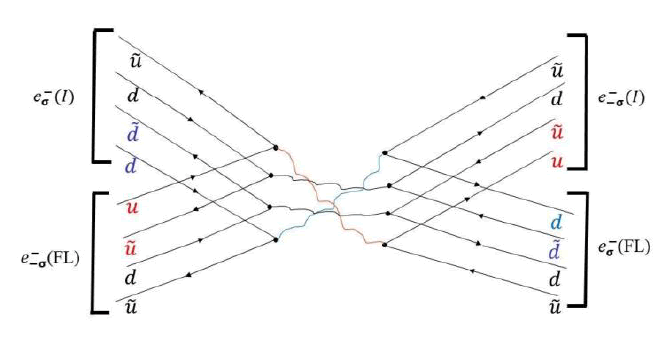
The MTJ read process may be explained in terms of the electron and pion tetrahedron gas model as follows: The initial non-polarized electron current has equal number of spin up and spin down electron tetrahedrons, u ddd and uduu. The non-polarized current flows through a first ferromagnetic layer we assume is polarized and let’s assume occupied mostly by uddd electron tetrahedrons. The scattering of two electron tetrahedrons of the same spin is elastic while the scattering of opposite spins creates the transition state complex of the two electrons with a pion tetrahedron “QCD glue” as illustrated in Figure 5. The collision process dissipates heat and cause a selective delay for one electron tetrahedron configuration.
FIG. 5. Illustrates the pion tetrahedron transition state complex “QCD glue” formed in a collision between two electrons with opposite spins.
The outcome is that the electron current has now higher percentage of uddd electron tetrahedrons that were elastically scatters with no delay, e.g. the electric beam is now polarized.
The polarized current enters the second ferromagnetic layer and the outcome will depend on the second ferromagnetic layer spin state. If it is dominated by uddd electron tetrahedrons, a favorable parallel ferromagnetic layer configuration (P), the quark exchange reactions will be elastic and a strong current will be measured. However, if the second layer magnetization is in Anti-Parallel configuration (AP), many more electron tetrahedron collisions with spin flips will occur, heat will be dissipated and the measured current will be smaller.
The electron and pion tetrahedron gas resistance model provides a mechanism that may explain why the magnetoresistance of two parallel ferromagnetic layers (P) is lower than the magnetoresistance of the Antiparallel (AP) configuration. The pion tetrahedron condensate in the ferromagnetic layer is polarized favorably and allows coherent elastic scattering of electron tetrahedrons with the same spin with no heat dissipation.
The pion tetrahedron condensate lattice model in a ferromagnet material may be an expanded model of the hydrogen atom, where multiple electrons share and move on the same pion tetrahedron condensate lattice sites. Electrons with the same spin are scattered elastically if they collide on adjacent lattice sites, while electrons with opposite spins may create a transition state complex, may exchange their spin states and are inelastic collisions.
Magnetic Random Access Memory (MRAM) is an emerging non-volatile semiconductor memory technology [12] expected to replace traditional computer memory based on complementary metal-oxide semiconductors. MRAM surpasses other types of memory devices in terms of nonvolatility, low energy dissipation and fast switching speed. Future developments in MRAM are based on spin-transfer torque. Spin transfer torque corresponds to the interaction of a spin polarized electronic current with the local magnetization. Magnetic moment is transferred from the conduction electrons to the magnetization resulting in a change of the magnetization orientation.
MRAM cells include a Magnetic Tunnel Junction (MTJ) that provides the write, read and bit storing functionality, essentially using two magnetic layers, Reference Layer (RL) and the Free Layer (FL), separated by a Magnesium Oxide (MgO) tunnel barrier. The two-bit storage states are the Parallel (P) and Antiparallel (AP) magnetization orientations. Topological insulators provide spin polarized current surface states due to the topology of the bulk band structure. The interplay of electron transport and spin dynamics provide a method to electrical control the magnetization state in Weyl semimetals.
According to the electron and pion tetrahedron gas resistance model described here, we propose a mechanism for the spin torque, where the spin switching in the magnetic Free Layer (FL) occurs due to electron tetrahedron scattering quark exchanges via the pion tetrahedron transition state complex as shown in Figures 5 and 6.
FIG. 6. Illustrates spin transfer torque by electron-electron scattering, where the upper electron represents a beam of spin polarized electrons e-(I) that flows through a free magnetic layer (FL) and are scattered by the FL electrons e-(I) via a pion tetrahedron transition state complex that decays and flip the electrons’ spins.
The upper electron represents a beam of spin polarized electrons e−(I) that flows through a free magnetic layer (FL) and arescattered by the FL electrons e- (FL) that we assume have an opposite magnetization state (AP). The two electron tetrahedronsexchange two quarks via the pion tetrahedron transition state complex and both plip their spin states. Assuming the initial spin state of the free layer was anti-parallel configuration (AP), (FL), after the scattering its spin is flipped up (FL) while thespin of the incoming polarized electrons that created the spin transfer torque is switched to the down state . The FLmagnetization state is switched from (FL) to (FL). Both u and d quarks need to be exchanged with the u and u quarks forthe spin exchanges.
A competing resilience against switching the magnetization state of the whole magnetic domain will occur where adjacent ferromagnetic electrons with opposite spins via the surrounding pion condensate will try to flip back the torqued spin.
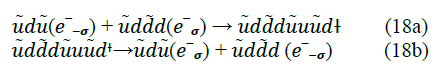
However, if the torque of the incoming electric current is strong enough, an inversion of the magnetic domain will occur and the opposite spin electrons will be pushed out from the inverted magnetic domain.
Kateel et al. showed that shaping the SOT channel to create a bend below the MTJ device causes an efficient and deterministic inversion of the spin of the FL magnetic domain.
Note that the double quark flavor exchange reaction creates a pion tetrahedron transition state complex “QCD glue” that dissipate heat to the pion tetrahedron condensate and may also create small vibrations of the pion tetrahedron lattice sites that are probably extremely small and negligible in low energies. However, in an extremely high-energy events, like black hole or neutron star binary mergers, the vibrations of the pion tetrahedron lattice may be the carry gravitation waves.
The pion tetrahedron condensate quark flavor exchange wave energy density in the vacuum with no matter particles is small, however, on cosmological scale it may still be significant. In the next section we propose a virtual box with a cosmological scale and propose that the vacuumpion tetrahedrons condensate non-matter should be included in Einstein’s energy-momentum tensor Tuv.
The pion tetrahedrons and Friedmann equation
Let’s imagine a virtual box in intergalactic space that has a very low density of free electron and pion tetrahedron gas and equal density of protons and neutrons gas for neutrality. Next let’s increase the box such that it includes for example the milky way galaxy with all its visible mass Mmilkyway and in it its center the supermassive Sagittarius A black hole with its mass MsgrA.
The Einstein-Hilbert action with a cosmological constant A is
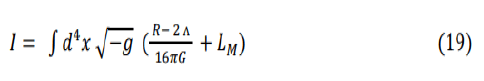
Where LM is the matter Lagrangian. Einstein’s field equation is obtained by the requirement that the action will be an extremum with respect to variation of the metric tensor guv.
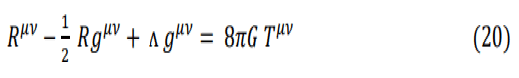
The energy-momentum tensor tuv is given by
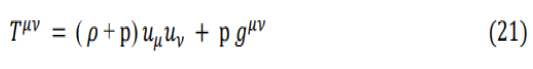
Where uu is the tangent velocity 4-vector, p is the matter-energy density and p is the pressure.
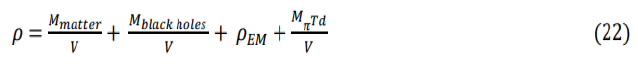
The matter-energy density includes the matter and black hole mass densities and the electromagnetic energy density of the milky-way galaxy. The vacuum pion tetrahedrons are not regular matter particles since they are composed of equal parts of matter and antimatter quarks and anti-quarks, however, since pion tetrahedrons are expected to be massive and to exchange quarks with matter particles they contribute energy to Einstein’s equation energy-momentum tensor Tuv.
The pion tetrahedron density MπTd/V=<w† uW† dWuWd> represents the pion tetrahedron tetraquarks, uddu, condensate. W†d isthe up quark creation operator, W†d is the down quark creation operator, and are the anti-up and anti-down quark creation operators.
Using the state equation, p=wp, with w=−1 for the expanding universe and Friedmann equation with k=1 the following expression for the matter-energy is obtained.
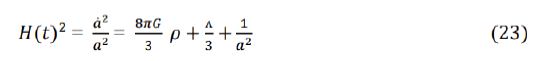
The matter-energy density ? is given in terms of the other variables as -

The pion tetrahedron condensate density MπTd/V is given by equations 7 and 9 as
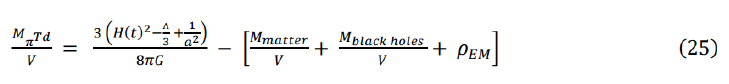
Equation 21 may give an estimate for the milky way galaxy pion tetrahedron condensate MπTd/V density assuming all other variables are known. A more direct method for calculating the pion tetrahedron mass is based on measurements of the time periodic variability of the B decay half-life times of radioactive nuclei’s in the perihelion and aphelion of earth’s trajectory around the sun. On cosmological scale and due to the huge intergalactic voids, the pion tetrahedron condensate energy density contribution to Einstein’s energy-momentum tensor and Friedmann equation may be significant. We suggest considering the possibility that the non-empty ground state pion tetrahedron condensate may replace the need to add dark matter and energy.
We note that the pion tetrahedron density is expected to be non-uniform and have an atmospheric like drop far from galaxy centers and that it may grow with time since the pion tetrahedrons are bosons that may be duplicated exponentially by Corley and Jacobson’s black hole laser effect. The pion tetrahedron density growth and the separation of matter and antimatter particles next to black holes event horizons may increase the energy density and pressure expanding the universe without adding dark matter and energy, where the additional antimatter may be trapped under the event horizon of the supermassive black holes.
The pion tetrahedron condensate may be a non-empty non-matter ground state QCD ether that can mediate the QED and QCD forces and probably gravity too since the pion tetrahedrons are massive and their density is expected to vary in space. QCD has a significant low-energy footprint and the quark flavor exchange wave may be an interesting example for the way QCD affects the dynamics of electrons.
References
- Burkert VD, Elouadrhiri L, Afanasev A, Arrington J, Contalbrigo M, Cosyn W, et al. Precision studies of QCD in the low energy domain of the EIC. Prog Part Nucl Phys. 2023;131:104032.
- Rom R. Non-uniform pion tetrahedron aether and electron tetrahedron model. J High Energy Phys Gravit Cosmol. 2024;10(2):810-824.
- Rom R. The quantum chromodynamics gas density drop and the general theory of relativity ether. J High Energy Phys Gravit Cosmol. 2023;9(2):445-454.
- Rom R. The pionic deuterium and the pion tetrahedron vacuum polarization. J High Energy Phys Gravit Cosmol. 2023;10(1):329-345.
- Sinova J, Valenzuela SO, Wunderlich J, Back CH, Jungwirth T. Spin hall effects. Rev Mod Phys. 2015;87(4):1213-1260.
- Mott NF. The scattering of fast electrons by atomic nuclei. Proc R Soc Lond Ser A-Contain. 1929;124(794):425-442.
- Mott NF. The polarisation of electrons by double scattering. Proc R Soc Lond. 1932;135(827):429-458.
- Santos TS, Mihajlovi? G, Smith N, Li JL, Carey M, Katine JA, et al. Ultrathin perpendicular free layers for lowering the switching current in STT-MRAM. J Appl Phys. 2020;128(11).
- Mihajlovi? G, Smith N, Santos T, Li J, Tran M, Carey M, et al. Origin of the resistance-area-product dependence of spin-transfer-torque switching in perpendicular magnetic random-access memory cells. Phys Rev Applied. 2020;13(2):024004.
- Yan B, Felser C. Topological materials: Weyl semimetals. Annu Rev Condens Matter Phys. 2017;8(1):337-354.
- Kurebayashi D, Araki Y, Nomura K. Microscopic theory of electrically induced spin torques in magnetic Weyl semimetals. J Phys Soc Jpn. 2021;90(8):084702.
- Kateel V, Krizakova V, Rao S, Cai K, Gupta M, Monteiro MG, et al. Field-free spin?orbit torque driven switching of perpendicular magnetic tunnel junction through bending current. Nano Lett. 2023;23(12):5482-5489.
[Crossref] [Google Scholar] [PubMed]