Letter to the Editor

, Volume: 7( 2) DOI: 10.37532/2320-6756.2019.7(2).175

• View PDF
• Download PDF

Photon's Red Shift from Distant Galaxies as the Evidence of Curved Time of Our Universe

*Correspondence:

Zlatan Stojanovic University of Banjaluka, Republic of Srpska, Bosnia and Herzegovina; E-Mail: szlatan@blic.net

Abstract

  

Introduction

There is one implication of the presented model which I would like to address the readers. When the energy of a photon decreases stepping away from the source (object) of gravitation (due to dilatation of space, and a decrease in time elongation), it also implies that the photon loses its energy because it is traveling by curved space i.e. curved radius. I have deliberately mentioned only space so that the image is easier to depict and to follow the logic. The decrease of energy of the photon is an indicator of how much space is curved. Of course, because the pace of time is also changing (gravitational time dilation), the time is also curved, and it contributes much more to the energy decrease. By radial traveling in a flat space-time (i.e. space-time far from the mass object) the photon would not lose its energy. The intensity of the decrease of photon energy is an indicator of how much our space is curved and how much our time is curved. The loss of energy of photon correlates with the strength of space-time curvature tensor. The more is the space-time curved, the more intense will be the loss in energy of the photon. To be more precise, the intensity of the change of photon energy is an indicator of space-time curvature (intensity of gravitational redshift and the intensity of gravitational blue shift).

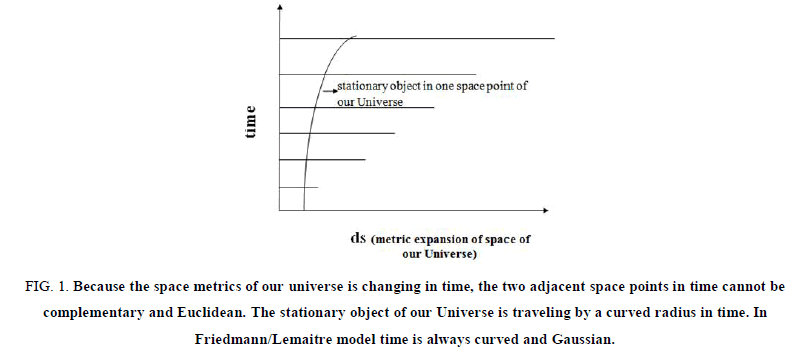
The photons of redshifts of distant galaxies lose their energy in the same way (because of space dilatation/metric expansion of space and the decrease in the time elongation/cosmological time dilation, during the evolution of our Universe). I emphasize during the evolution of Universe which refers to the evolutional time of our Universe. Try to imagine one stationary object in the one space point of Friedmann/Lemaître Universe, where the pace of time is the same. Space point (where the object is positioned) cannot be complementary and Euclidean to the next space point in time because space of our Universe is changing its metrics (during evolution). Two space points are not complementary and Euclidean in time if we have the change of space metrics (FIG. 1). I must underline that I am not speaking of the curvature throughout the space i.e. transversely. I am depicting the space longitudinally in time. Because our object is stationary in the space the one conclusion imposes by itself. The object is traveling in time by a curved radius i.e. the time is curved. So, the time in Friedmann/Lemaître model(s) is always curved and Gaussian. I think that the physicists who are working on Friedmann/Lemaître model(s) should take into consideration this phenomenon because I am not sure how much the proposed model is complementary with Friedman's time coordinate and the equations derived.

When we have the change of space metrics, the time always changes its metrics (pace) e.g. cosmological time dilation. Contrary to the Masreliez's approach I propose forward accelerating the time of our Universe. This intrinsic property and asymmetry of time could explain time direction (time's arrow) without the need for entropy. The forward accelerating time could be in accordance with the acceleration of our Universe because of the relationship between the metrics of space and time bound by the speed of light c.

Now recall: the intensity of decrease of energy of the photon is an indicator of how much space-time is curved. So, by the loss of photon energy in the case of redshifts of distant galaxies we know that our Universe is curved in its evolution. But we must be careful in the interpretation of what does it mean. The decrease of energy of a photon is partially caused by the change of space metrics and partially by the change in time metrics of our Universe. The photons of redshifts of distant galaxies lose their energy because they travel in time by the curved radius. To depict it better, there is one good analogy with Einstein's rotating disk, but it needs some modifications. The curved radius of the rotating disk has implied that space is curved. The farther we are from the disk's center space is becoming more contracted (ds2 on the periphery<ds1 in the center) and the pace of time is becoming elongated (dt2 on the periphery>dt1 in the center). Now, we will inverse the disk's gravitational field. In such gravitational field, the farther we are from the disk's center the space metrics is more expanded (ds2 on the periphery>ds1 in the center) and the time is less elongated i.e. faster (dt2 on the periphery<dt1 in the center). Imagine that we are living on the circle at some distance from the disk's center. We will call it closed string. This string has its space metrics (ds1) and its time metrics i.e. pace (dt1), which are the same on the whole string because we are on the same distance from the disk's center. Imagine that we are stationary on that string. Because we know that our Universe evolves, the string stretches itself from the center to the periphery of the disk. Now we will take another string which is more distant from the disk's center in regard to the first string. This string has expanded space metrics (ds2) and its time is faster in relation to the first string (dt2). The curved radius of the disk between these two strings does not represent the curved space, because our string has evolved through the time. We can term this curvature as the curvature of space in time (longitudinal curvature). But because we are in a stationary state and we are traveling in time by a curved radius (as in previous example; Graph 1) it implies that the time of our Universe is curved and Gaussian.

How can we determine this kind of curvature of our Universe? The answer is by our measuring sticks and clocks which are the both represented in the photon. Light has its wavelength (stick) and wave frequency (clock), so we can measure both parameters (like in gravitational shift). The decrease of energy of a photon is partially caused by the change of space metrics and partially by the change in time metrics of our Universe. I must be a little clearer because the wavelength and frequency of the photon are interconnected. If we have an only expansion of space i.e. dilatation of space metrics the energy of photon will decrease due to the increase of its wavelength. At the same time, we will have and loss in the frequency, but the loss in the frequency is not caused by the change in the time metrics. Likewise, when the photon is sent from the reference system with only elongated time toward us, the energy of photon will be lower because the frequency of the photon is lesser. Interconnection will cause the wavelength to be increased. But the change of the wavelength is not caused by the change of space metrics. So, I will repeat: the photons of redshifts of distant galaxies lose their energy because of the both: the space dilatation and the decrease in the time elongation during the evolution of our Universe. By the loss of energy of photons in the case of redshifts of distant galaxies, we know that our Universe has the curved time.

By the decrease of photons' energy of redshifts from distant galaxies, we will ascertain how much our space was contracted and time elongated in the past. By the intensity of that decrease in time, we will ascertain how much the time of our Universe is curved. As I have mentioned earlier the loss of energy of photon correlates with the strength of space-time curvature tensor.

By this approach, the question of curvature throughout the space i.e. transverse curvature (flat, saddled, closed) is not ascertained. But at least, it is on the track of De Sitter, how empty 4d spacetime can be curved.