Research
, Volume: 11( 4) DOI: 10.37532/2320-6756.2023.11(4).333Mercury in a Quantum-Gravitational Field
- *Correspondence:
- Paul R. Gerber
Gerber Molecular Design, Forten 649, CH-8873 Amden, Switzerland,
E-mail: Paul.Gerber@moloc.ch
Received date: 17-February-2023, Manuscript No. tspa-23-89565; Editor assigned: 22-February-2023, Pre-QC No. tspa-23-89565 (PQ); Reviewed: 28-February-2023, QC No. tspa-23-89565 (Q); Revised: 15-March-2023, Manuscript No. tspa-23-89565 (R); Published: 1-April-2023, DOI. 10.37532/2320-6756.2023.11(4).333
Citation: Gerber P. R. Mercury in a Quantum-Gravitational Field. J. Phys. Astron.2023;11(4):333.
Abstract
A scalar field theory of gravitation yields the correct perihelion precession of Mercury’s orbit around the sun. We present the corresponding theory and numerical calculations for the relativistic Kepler problem. Furthermore, it turns out that the concept of gravitational potential cannot be maintained in the relativistic case because acceleration becomes velocity-dependent. In addition, in extreme cases, like large distances from a gravitational center or for high velocities of a body, the gravitational forces become also dependent on the direction of the body’s velocity.
Keywords
Relativity; Gravitation
Introduction
According to Classical Mechanics the planet Mercury circles the sun in an elliptical orbit. However, measurements show a systematic deviation. After removing the effects of perturbations by the other planets one calculates a remaining rotation of the ellipse’s perihelion of 43 arc-seconds per century. General Relativity (GR) yields a value for this perihelion precession, pt (in radians per revolution), of,

Where L is the semi-latus rectum of the ellipse, and s the Schwarzschild radius of the central star. The reduced precession, pr turns out have a value of one. The corresponding value agrees perfectly with measurements, and this is considered the most accurate test of GR [1]. However, GR as a theory has a few problems. It cannot be quantized in a conventional field-theoretical treatment; it is not renormalizable. Furthermore, it turned out, that the gravitational waves it should proposedly support, violate fundamental requirements of plane waves [2]. In addition, it is not decided whether the cosmological read-shift originates in space expansion as proposed by GR or whether it is a damping of light caused by acceleration in the varying gravitational field in space [3]. For these reasons one may suspect that there must be an alternative explanation of Mercury’s perihelion shift.
Gravitational Field of a Star
In a scalar-field theory, the field of a star is described as a flow of gravitons and anti-gravitons in radial direction [4-6]. The strength of the field at a concentric spherical surface is determined by the number of gravitons that cross the surface per time unit and per area. This area increases with the square of the distance such that the strength of the field decreases with the inverse square of the distance, as stated by Newton’s law of gravitation. In this theory, the gravitational force on a test body is determined by “reflection” processes of anti-gravitons to gravitons by the body, and vice versa for a test anti-body [4]. Actually, the stars field is also maintained by a continuous process of such reflections at the star’s constituent particles from incoming anti-gravitons to outgoing gravitons. This maintains an outgoing mass out-flow without any energy flow [5].
Graviton-Reflection Process
Gravitons of the star’s field move away from it and anti-gravitons towards it; there is no net flow of energy. However, we have an outward mass flow because anti-gravitons have negative mass. Thus, a body’s reflection process from an anti-graviton to a graviton corresponds to a large momentum transfer to the body directed towards the star and to a small energy transfer which can be positive or negative, depending on the direction of the body’s movement with respect to the field’s direction. The actual transfer values are governed by the individual reflection processes.
The energy-momentum 4-vectors of graviton and anti-graviton read,

where the 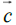 are unit vectors and the ν' s are the absolute wave numbers of the quanta, with values in the range of 2×104 cm-1 (corresponding to the sun’s surface temperature) to about 2×107 cm-1 (estimated temperature at the center of the sun). This is eight to
five orders of magnitude smaller than the mass of a proton (~4×1012 cm-1). The speed unit-vector
are unit vectors and the ν' s are the absolute wave numbers of the quanta, with values in the range of 2×104 cm-1 (corresponding to the sun’s surface temperature) to about 2×107 cm-1 (estimated temperature at the center of the sun). This is eight to
five orders of magnitude smaller than the mass of a proton (~4×1012 cm-1). The speed unit-vector 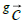 points away from the star while
points away from the star while 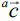 points towards it. For the present purpose, we set:
points towards it. For the present purpose, we set:

An intelligible assumption that will be discussed below.
In our inertial system the star is at rest and we neglect the star’s movement caused by the acceleration of the moving body because the rest-mass ratio can be made arbitrarily small. We consider a single “reflection” process in this system. Conservation of momentum yields,
where  is the momentum of the body. With its energy e, energy conservation reads:
is the momentum of the body. With its energy e, energy conservation reads:

We now have to consider the graviton energies (wave numbers). Their values in equations (4) and (5) are the ones experienced by
the body in its rest system. The body moves with a velocity  , such that, due to Doppler-shift, it experiences,
, such that, due to Doppler-shift, it experiences,

when measured in the stars rest system, where we set up the scattering process. Here, the (anti-) gravitons wave-numbers are termed vs with a (star-) subscript. In equation 6 we have the usual definition of,

and the angle θ between the direction of the body’s speed,  , and the direction of the motion of the gravitons (radial). The important
thing to realize here is that the gravitons, generating the stars field, move away from the star, whereas the compensating anti-gravitons
move towards the star [5], such that their corresponding θ -values differ by π! Thus, equations (4) and (5) yield,
, and the direction of the motion of the gravitons (radial). The important
thing to realize here is that the gravitons, generating the stars field, move away from the star, whereas the compensating anti-gravitons
move towards the star [5], such that their corresponding θ -values differ by π! Thus, equations (4) and (5) yield,
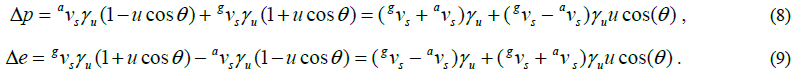
Now, one must also realize that for every process with given values of 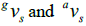 there exists a process for which the two values
are interchanged. These two processes have equal weights in a stationary field, hence equations (8) and (9) can be reduced to,
there exists a process for which the two values
are interchanged. These two processes have equal weights in a stationary field, hence equations (8) and (9) can be reduced to,

Cross Section
A further important point to realize is that the cross section is independent of the speed 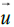 , because we must consider the
body as a quantum field
, because we must consider the
body as a quantum field  which is scaled up by a factor
which is scaled up by a factor 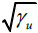 as u increases, while the body experiences a
corresponding length contraction [4]. These two effects compensate each other and thus yield a speed-independent
gravitational cross section of the body. Correspondingly, we may describe the body by a mass parameter, independent of
the body’s speed.
as u increases, while the body experiences a
corresponding length contraction [4]. These two effects compensate each other and thus yield a speed-independent
gravitational cross section of the body. Correspondingly, we may describe the body by a mass parameter, independent of
the body’s speed.
Effect of the Gravitational Field
Now, we can summarize everything because the relativistic effects are peeled out by the factor 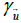 in equations (10) and (11). In the
limit
in equations (10) and (11). In the
limit 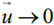 we have the non-relativistic acceleration. The whole nasty rest describing the star’s gravitational field can be lumped
together into the Newtonian expression, the star’s Schwarzschild radius. In summary, the relativistic effect in the star’s rest system
consists in multiplying the body’s (Newtonian) acceleration by a factor γu .
we have the non-relativistic acceleration. The whole nasty rest describing the star’s gravitational field can be lumped
together into the Newtonian expression, the star’s Schwarzschild radius. In summary, the relativistic effect in the star’s rest system
consists in multiplying the body’s (Newtonian) acceleration by a factor γu .
Finally, one must realize that in the star’s rest system time-steps have also to be multiplied by a factor γu (inverse time-dilatation); this, in calculating the speed change as well as the position change.
Numeric
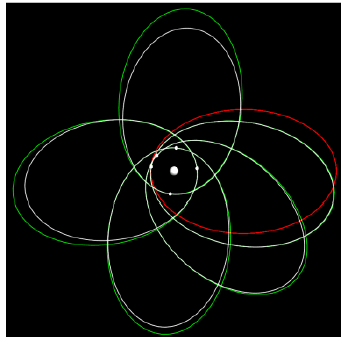
The equations were solved (integrated) numerically. The following figure shows a few runs for the relativistic Kepler problem. Parameters are chosen to yield a Kepler orbit with an eccentricity e=0.75. The body moves clockwise, as does the periastron shift. Each run was stopped after 70 turns. In red the non-relativistic Kepler orbit is shown which also was the (approximate) first orbit of all runs. The last orbit of each run is shown in white, while the green curves show the corresponding orbit for the non-relativistic case. Parameter of the runs is the velocity at the periastron, vpa and results are given in TABLE 1 and illustrated in FIG. 1:
TABLE 1. See text below for legend.
| vpa/c | p[0] | pr | efit |
|---|---|---|---|
| 0 | 0 | 0.75 | |
| 0.05 | 10.3 | 1 | 0.749 |
| 0.1 | 41.7 | 1.01 | 745 |
| 0.15 | 95.3 | 1.02 | 0.739 |
| 0.2 | 173 | 1.03 | 0.73 |
| 0.25 | 279 | 1.05 | 0.718 |
Curves can be identified by the periastron shift, p which is given in degrees. The reduced periastron shift, pr see equation (1), tends towards a value of one for low values of vpa . This agrees with the value measured for Mercury ( vpa/c = 0.0002) . In evaluating pr we took the value L from the Kepler-orbit (green). The last row shows the eccentricity, efit of an ellipse fitted to the last turn (in white). For the sake of accuracy the values in the table are determined from runs with 600 turns. Accuracy is mainly determined by locating the periastron, which becomes less important for larger numbers of turns. We also have varied the eccentricity in the runs from values of 0.1 to 0.9 and for small velocities (vpa /c = 0.02 0.07) to .The results yield consistently values pr =1.00.
Discussion
The proposed spin-zero gravitational field theory, allows to calculate the orbit of a small body in a star’s gravitational field by considering scattering processes between the body and the gravitons and anti-gravitons of the stars field [4]. The observed periastron shifts of elliptic orbits are well reproduced. There are several important aspects:
• A scattering process must include a graviton and an anti-graviton because of graviton conservation.
• The Doppler-shift of the field quanta for the moving body is opposite for gravitons and anti-gravitons.
• The time-dilation effect must be taken care of when integrating the equation of motion.
These calculations neglect damping effects, which may originate e.g. from the generation of gravitational waves by accelerating the body out of its own gravitational field. Actually, these may be important for the relatively high velocities, vpa considered in the present calculations. However, we have chosen high values because they yield more-illustrative effects. The negative-mass concept proves to be essential in guaranteeing a conservative motion (transition from (8, 9) to (10, 11)) [6].
Breakdown of the Concept of a “Potential”
It is obvious from the summary section after equation (11) that the concept of a gravitational potential cannot be maintained when
one proceeds from classical to relativistic considerations; the acceleration becomes velocity dependent (factor 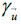 ). Furthermore,
approximation (3) assumes that the star’s field distribution does not change perceptibly when directions of graviton and anti-graviton
disagree slightly. In the non-relativistic case these directions agree. In the relativistic case and for non-zero speed, u, they are subject
to relativistic aberration. Thus, we must rely on the above assumption about the stars field (-distribution). This assumption may break
down for two different reasons, which, however, play together:
). Furthermore,
approximation (3) assumes that the star’s field distribution does not change perceptibly when directions of graviton and anti-graviton
disagree slightly. In the non-relativistic case these directions agree. In the relativistic case and for non-zero speed, u, they are subject
to relativistic aberration. Thus, we must rely on the above assumption about the stars field (-distribution). This assumption may break
down for two different reasons, which, however, play together:
• The star’s field at a given point has strong directional dependence, which may be caused by a large distance from, and a small radius of the star.
• The body’s tangential component of speed is large leading to large directional aberration.
Obviously, this aberration disappears for exact radial movement of the body. Consequently, the experienced force depends on the direction of movement and, thus, can also not be described by a gravitational potential. The above mentioned breakdown-reasons are most probably the explanation for the “abnormal” galaxy rotation curves, which are very well explained by the concept of Modified Newtonian Dynamics (MOND) [7-10]. Actually, MOND considers accelerations of circularly moving bodies and we may question here whether it can be generalized to cases of arbitrary directions of movement by assuming a corresponding gravitational potential.
Conclusion
This work presents evidence that a scalar field theory of Gravitation yields results which reproduce experimental findings that are conventionally considered to be an exclusive consequence of the theory of General Relativity. Furthermore, it shows that potential energy is a non-relativistic concept which cannot be maintained in the relativistic case. Quantization of gravity turns out to be a quite straightforward procedure in contrast to GR’s geometric approach to gravity. Furthermore, it is suggested that the mandatory abandoning of the concept of potential energy may justify MOND’s explanation of galaxy rotation curves, which conventionally require to introduce the concept of (elusive) dark matter.
References
- Weinberg S. Gravitation and Cosmology.Wiley:1072
[Google Scholar] [Crossref] - Gerber P. R.On the Polarization of Gravitational Waves, viXra:2001.0398;2020
[Google Scholar] [Crossref] - Gerber P. R.,Cosmological Redshift from Light Acceleration, viXra:2210.0118;2022
[Google Scholar] [Crossref] - Gerber P. R.On Quantum Field Theory and Gravitation, viXra:1911.0010;2019
[Google Scholar] [Crossref] - Gerber P. R. Static Fields as Mass-Currents and Mercury's Perihelion Shift, viXra1505.0078;2015
[Google Scholar] [Crossref] - Gerber P. R.Physics with Negative Masses, viXra:1303.0100;2013
[Google Scholar] [Crossref] - Rubin V. Bright galaxies, dark matters. Springer Sci. Bus. Media; 1996.
[Google Scholar] [Crossref] - Milgrom M. A modification of the Newtonian dynamics-Implications for galaxies. Astrophys. J. 1983;270:371-83.
[Google Scholar] [Crossref] - McGaugh SS. A tale of two paradigms: the mutual incommensurability of ΛCDM and MOND. Can. J. Phys. 2015;93(2):250-9.
[Google Scholar] [Crossref] - Gerber P. R.On MOND’s Missing-Mass Problem in Galaxy Clusters, viXra:2205.0094:2022
[Google Scholar] [Crossref]