Original Article
, Volume: 5( 2)Launching Jets From the Transitive Layer of Accretion Disks by Burgers Vortex
- *Correspondence:
- Abrahamyan MG Department of Physics, Yerevan State University, Yerevan, Armenia, Tel: 0542 236 8558; E-mail: mabr08@mail.ru
Received Date: April 21, 2017 Accepted Date: May 9, 2017 Published Date: May 18, 2017
Citation:Abrahamyan MG. Launching Jets From the Transitive Layer of Accretion Disks by Burgers Vortex. J Phys Astron. 2017;5(2):111.
Abstract
Possibility of representation of a transitive (boundary) layer of an accreting disk round young stellar formations as Burgers vortex with a converging radial flow of substance, almost homoge- neous rotation in nuclear area which is falling down on the hyperbolic law to periphery is consi- dered. Physical and geometrical characteristics of a transitive layer are received. It is shown that transitive layer of Burgers, in depending of characteristics of transitive layer can both to provide formation of bipolar collimated outflow which is accelerated proportionally to the vertical co- ordinate accruing in due course exponentially (the active phase) and provide the capture of all accreting substance by the central body. The behavior of outflow is determined by the properties of Burgers vortex.
Keywords
Accretion disk; Burgers vortex; outflow
Introduction
Process of formation of stars leads to occurrence accretion disk (AD) around "young star formations" (YSO) [1]. Almost all such objects which have reached of age of an order of one millions of years possess such disk [2]. Opening of gas and dust clouds round protostars and of T Tauri stars [3] confirms this conclusion. The mechanism of formation of stars and structures accompanying them of type accretion disks and bipolar outflows so far is not clear [4,5]. A problem of the angular momentum - the mechanism, on which accreting substance loses the angular momentum to rich a star, mechanisms causing macroscopic turbulence, and the viscosity connected with it, occurrence astrophysical, as a rule, bipolar, collimated jet eruptions from an accretion disk’s central region, remain in the center of attention of many researchers. It is considered, for example, that the angular momentum is broken by a solar wind at T Tauri stage, and then broadcast to external areas of a disk by viscosity [6]. Viscosity is created by large-scale turbulence, but mechanisms causing turbulence, for the present are not completely clear... As to jet eruptions, which are observed from not relativistic HH objects [7] to relativistic micro-quasars and gamma bursts (see for example, [8,9]), and to extragalactic streams of Mpc scales from active galactic nucleus [10], though the propagation and collimation of jets it is possible to consider as rather clear [11,12], the exact mechanism of their formation remains unclear. Discussed magnetic mechanisms connect generation of jets with interaction of a rotating matter in internal areas of accretion disk with a magnetic field of the central star, or an external magnetic field (see for example [13-16]). In thermal (see in [17]) mechanism the stream generation is connected with interaction of accretion currents with the central star in a disk boundary layer. In hydrodynamic vortical mechanisms [18-21] the features of an outflow are defined by properties of a vortex, similar to tornado occurrence. Other hydrodynamic mechanism has been offered by authors [22] who have noticed that assumptions for thin accretion disk approach, where orbits should be circular, are broken from certain critical radius. It leads to occurrence of a quasiradial stream of substance in a disk and to occurrence of the jet expiration (references of earlier attempts can be found in [22]).
We recognize the importance of magnetic fields in physics of outflows from YSO. Indeed, magnetic fields of considerable magnitude were indirectly and even directly detected in the vicinity of some YSO’s and also in outflows (see, e.g., [23]). Their role in collimation of outflows is evident from these observations. However, an important observational conclusion that X-ray properties YSO’s were unrelated to the presence or lack of outflows [24] is pretty awesome, if outflows are determined dynamically by magnetic field is true.
In the present work we continue to develop the vortical concept, and we will try to present central regions of accretion disks in the form of Burgers vortex. This vortex is one of a few axially symmetrical exact solutions of the Navier-Stokes equation, which is often used for the description of different properties of a tornado, and also widely used in the researches devoted to turbulence occurrence, etc. (see for example [25]).
Modelling of accretion disk by Burgers vortex
The system of Navier-Stokes and continuity equations for axially symmetrical currents of the viscous environment round the central body of mass M* in cylindrical co-ordinates r, θ, z is represented as:
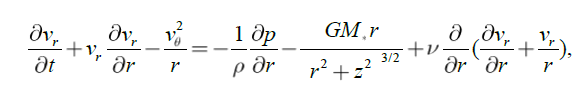 (1)
(1)
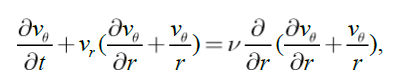 (2)
(2)
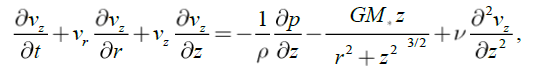 (3)
(3)
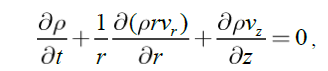 (4)
(4)
where ν is kinematic viscosity, ρ is homogeneous mass density, p is the pressure. In the resulted equations because of axial symmetry of a problem the terms containing derivatives rather θ, and also derivatives vr and vθ with respect to co-ordinate z are omitted.
In case of homogeneous distribution of a mass the stationary continuity equation (4) allows the exact solution vr = - Ar, vz = 2Az. (5)
Corresponding azimuthal equation of motion (2) under the condition
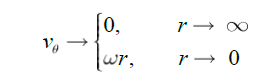 (6)
(6)
gives following expression for azimuthal speed
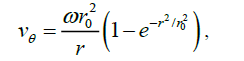 (7)
(7)
where ω has meaningful to angular speed of homogeneous rotation of nuclear area of a vortex, and r0 ≡ √ (2 ν/A). (8)
Formulas (5) and (7) represent one of a few exact axially symmetrical solutions of Navier-Stokes equation that is the Burgers vortex.
Azimuthal speed (7) has a maximum, vθmax = 0.6382 ωr0, which reaches at rm 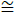 1.12r0. (8)
1.12r0. (8)
The characteristic size r0, apparently from (8) is defined by kinematic viscosity ν and a gradient of speed of radially converging stream A which simultaneously characterizes also vertical bipolar outflow of substance from nuclear area of the vortex.
Typical rotary speed of a surface of the central body of radius R* (in terms of R ) and cycle time P (in days), an order
) and cycle time P (in days), an order
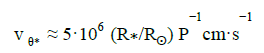 (9)
(9)
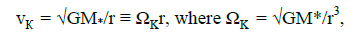 (10)
(10)
which on the surface of the central body, an order
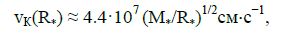 (11)
(11)
where M* is the mass of the central body in terms M*. The rotational velocity of the accreter is less than the Keplerian one. A difference between these speeds, generally speaking, is an order of Keplerian speed. This is an enormous burden to place on the substance, slowing down over relatively short distance to become synchronous with the surface. Therefore in this area should operate significant forces of a friction and must be released a big amount of energy.
The internal area of a disk in which occurs this transition, is transitive (boundary) layer (TL) of a disk. It is clear that in this area the crucial role played by viscosity and pressure.
In the present work we will try to provide the transitive layer in the form of Burgers Vortex. This requires that the rotational speed of the Vortex at distance R* ≪ r coincided with the central body surface speed v*:
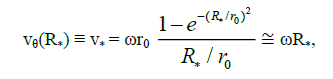 (12)
(12)
that is, ω is the angular velocity of rotation of the surfaces of the central body, and on the outer border of TL the Vortex speed (7) should smoothly go into Keplerian (10). This gives
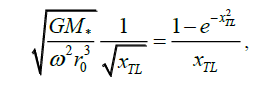 (13)
(13)
where xTL ≡ rTL/r0.
On the schedule Figure. 1 curves represent the rotational profiles of Burgers vortex (a continuous curve in the left with faltering continuation on the right) and of Kepler. The contact of these curves occurs at following value of dimensionless parameter a:
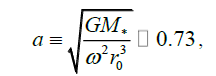 (14)
(14)
In a point (Figure. 1)
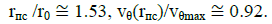 (15)
(15)
Hence, the disk transitive layer, modeled as Burgers vortex, represents a ring with the radial sizes 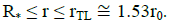 This size may vary from a few to a dozen R∗. For example, for the central body with the parameters of the Sun, the size of the
transitive layer would be of order ~30R*.
This size may vary from a few to a dozen R∗. For example, for the central body with the parameters of the Sun, the size of the
transitive layer would be of order ~30R*.
Parities (14) and (15) allow expressing the maximum speed of rotation of a vortex in mass of the central body and the characteristic size rm:
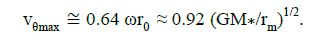 (16)
(16)
By integration of the radial (1) and vertical (3) equations, taking into account (5), (7) the pressure distribution in a transitive layer, under a condition p (R*, 0) = p*, we will receive
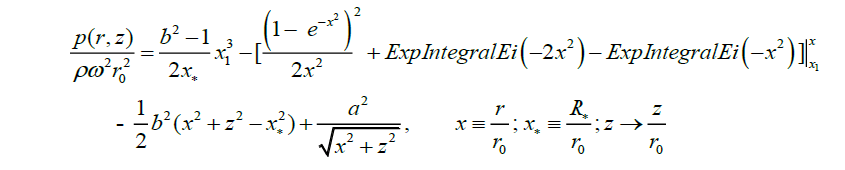 (17)
(17)
where b ≡ A/ω, and p*/ρ has been estimated from the Clapeyron equation:
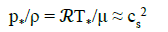 (18)
(18)
where T* and cs* are temperature and the sound speed on the surface of central body respectively,  = 8.3·107erg·mol-1K-1 is
the gas constant, μ is the molar mass of gas. In (17) is used notation (14).
= 8.3·107erg·mol-1K-1 is
the gas constant, μ is the molar mass of gas. In (17) is used notation (14).
Surface on which the gas pressure vanishes describes by equation:
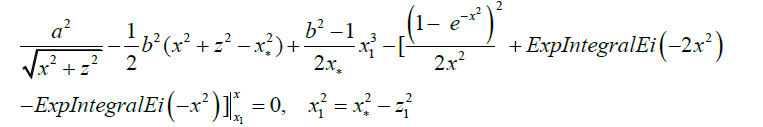 (19)
(19)
The solution of this equation rather z: zTL = z (x), gives semi thickness of TL depending on radial co- ordinate in units r0.
Some properties of a disk with Burgers TL
Accretion rate - the quantity of substance radially transferred through a disk for a time unit dm/dt=m-2πrρvr h (r), (20)
where h is a thickness of a disk, ρ is the mass density, vr is the speed of the radial flow of substance. In a two-dimensional case, the joint decision of the equation of a continuity (4) and the radial equation of the angular momentum, taking into account (15), that is lawful only in area r> rпc, where it is possible to neglect vertical speed, gives the formula for radial speed [26]:
vr = - 3 ν/2r. (21)
In this case actually it is considered that the transferable all mass (20) riches to a star and increases its mass:
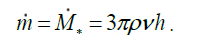 (22)
(22)
Estimations of Reynolds number show that accretion disks are turbulent. For an estimation of turbulent viscosity in them usually use α - parametrization of a disk [26]:
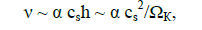 (23)
(23)
where α - dimensionless parameter with value from zero accretion is absent) to unit.
For an accretion rate in the Burgers transitive layer, taking into account (5) and (8) we receive
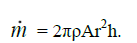 (24)
(24)
Let's notice the important feature of Burgers TL that is how is nearer to the center of a disk, the lesser radial transfer of mass. Instead the mass transfer in a vertical direction increases significantly.
Formation of a bipolar outflow
Current function of axially symmetrical vortex ψ(r,z) for Burgers vortex gives
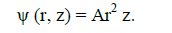 (25)
(25)
The characteristic form of a surface on which current function of the Burgers vortex has constant value, is represented on For definition of a trajectory of gas particles it is necessary to solve equations
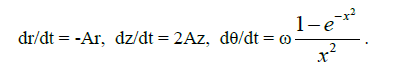 (26)
(26)
First two equations, considering initial conditions r(0) = rTL and x(0) = z0 give
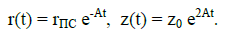 (27)
(27)
Integrating the third equation we will receive time dependence of the azimuthal coordinate θ:
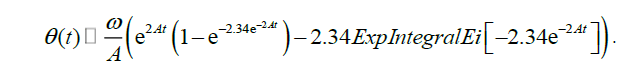 (28)
(28)
On the fig. 4 the lines represent dependence of azimuthal angle from dimensionless time 2At. In zero approach these lines can be approximated by linear function
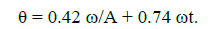 (29)
(29)
Excluding of time from (27) and (29), we will receive the equation of a spatial curve (trajectory) by which approaches to the center of a disk gas in the Burgers transitive layer:
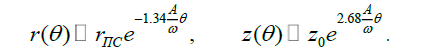 (30)
(30)
Hence, gas particles come nearer to the disk center by a helicoid trajectory, which characteristic form is presented on fig.5, and create a bipolar outflow. Speed of the stream is accelerated proportionally to vertical co-ordinate z which grows in due course, and the radial co- ordinate decreases exponentially.
It is necessary to notice that formation of the bipolar outflow begins in the area, closer to the internal boundary of the transitive layer, and the behavior of jet is determined by the properties of Burgers vortex, although the parameter ω is associated with the mass of the central body.
he mass of substances falling on central body per The mass of substances falling on central body per second can be estimated using the equation (24) on the inner border of the TL:
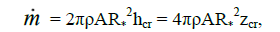 (31)
(31)
where zcr is the maximal high on the border r = R∗, on which gas captured by the central body. Obviously

which gives for zcr transcendental equation
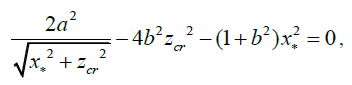 (32)
(32)
where zcr is measured in units r0.
Solutions of this equation for the value b = 0.7 are presented in Fig. 6, which implies that 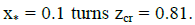 Whereas
for the thickness of the TL equation (19), when
Whereas
for the thickness of the TL equation (19), when 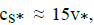 gives
gives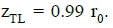 It follows that only 0.2 part of accreting
substance comes on the formation of a bipolar outflow, the rest is captured by a central body.
It follows that only 0.2 part of accreting
substance comes on the formation of a bipolar outflow, the rest is captured by a central body.
Estimation of the accretion rate of the central body in this case, for ρ ~ 10-12 g · cm-3, gives
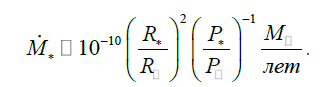 (33)
(33)
With the change in the values of parameters cs* and (b) the proportion of mass, going on the formation of the bipolar Jet changes. For example, for constant values x* and b, with a reduction of the speed of sound, the thickness of the TL is decreased, whereas zcr does not change. This reduces the mass of the jet formation. At even smaller valuescs* outflow from such systems will be absent: the whole accreting mass will be captured by a central body. A similar picture can be obtained and at the same time reducing the b parameter. Consequently, in the course of evolution, the systems may have periods of "activity" with the eruption of the bipolar outflow.
Effective Surface Temperature
Energy dissipation in unit of volume of a disk for a unit time because of a viscous friction, is estimated by the formula
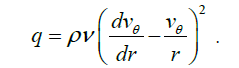 (34)
(34)
Out of a transitive layer of a disk taking into account (16) it gives
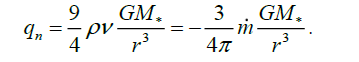 (35)
(35)
Considering that this energy is radiated from both edges of a disk under the black body law, we receive the well-known dependence of effective surface temperature of a disk on radial co-ordinate [27]:
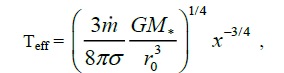 (36)
(36)
where 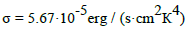 is the Stefan- Boltzmann constant.
is the Stefan- Boltzmann constant.
For an estimation of temperature of a transitive layer, we will take advantage that luminosity of accretion substances in the field of gravitation of the central body is released in a optically thick transitive layer
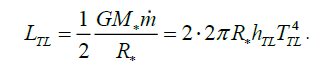 (37)
(37)
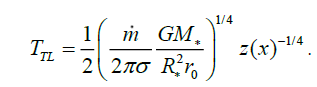 (38)
(38)
Characteristic dependence of effective temperature of accretion disc (functions z (x)-1/4 and x-3/4)
from dimensionless radial co-ordinate x is presented on the schedule fig. 6, where δ dimensionless parameter is equal (12·x2 ). The effective temperature in a transitive layer has flat character, and crosses a curve ~x-3/4 in limits of TL. These considerations only tell us about the surface temperature. The internal temperature that determines the disk thickness h and probably also the viscosity in the disk can be quite different, and depends on the mechanism transporting energy to the surface. But this transport needs to some detail for realistic disk models and when a number of additional assumptions are made...
Stability of a Disk
Let's notice that for the Burgers vortex the value (rvθ)2 increases in a direction to periphery of a transitive layer (Reyleigh criterion for stability of axially symmetrical currents):
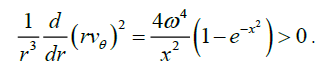 (39)
(39)
Gravitational stability of differentially rotating disk is defined by the criterion of Toomre [28]
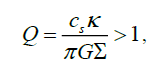 (40)
(40)
where Σ is superficial mass density of a disk, κ = 2 Ω√ (1+Ωʹr/2Ω) is epicyclical frequency. In area of Keplerian rotation (40) gives
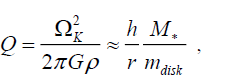 (41)
(41)
which shows, that the outer edge of a disc can become unstable. Instability of outer edge is found in 2D numerical simulations of accretion discs also [29,30].
In a transitive Burgers layer for Toomre parameter we receive expression
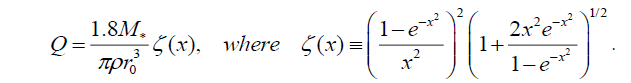 (42)
(42)
The least value, ≈0.2, the function ζ(x) accepts on external edge of TL, r = rTL. So the considered area of a disk is stable if 1.8M* /πρr03 > 5. If to consider r0 an order of several radii’s of the central body this condition is satisfied for transitive layers of typical accretion disks.
Conclusion
The results received in the present consideration, specify in importance of hydrodynamic vortical processes for physics of accretion disks. In particular, the description of the central transitive layer of a disk by the Burgers vortex allows explaining formation of bipolar outflows without attraction of magnetic fields, or the powerful thermal phenomena which, from our point of view, in an initial stage of star formation are not too important.Qualitatively, vortical hydrodynamic process of formation of bipolar outflows, apparently, occurs under the following scenario. The Radially-converging stream in Keplerian disk, leads to "accumulation" of the angular momentum. Because of a viscous friction between gas blankets, the part of the angular momentum has to be transferred outside. The rest changes the character of Keplerian rotation in its central part at the expense of excessively big turbulent viscosity, energy dissipation and pressure gradient force. A transitive layer in form of a large-scale Vortex with almost uniform rotation in its nuclear area, a fact which is observed in many discs [18], is forming. Continuing to move toward the center, depending on values of the parameters of the transitive layer, a substance with excess of angular momentum and energy generates highspeed bipolar Jet, accelerating on vertical direction (active phase), and the rest of substances lost angular momentum and energy falls on the emerging central body increases its mass and speeds up the process.
The formation of the bipolar Jet begins in the area, closer to the internal border of transitive layer. However, depending on the values of the physical parameters of the system, the bipolar Jet may not occur: all the accreting mass will be captured by the central body.
In this consideration parameters of Burgers vortex are constants. The following work we plan to take into account no stationarity of transitive layer, as well as a comparison of theory with observations.
References
- Philippe A. EUVE observations of VW Hydri in Super-outburst. Ap. J. 1994:420;837.
- Karl HE. Observational clues to brown dwarf origins. Ap. J. 2001:553;153.
- Deborah PL. On the composition and printings of the Debgter sngon po by ’Gos lo tsā ba gzhon nu dpal. Astronomical Journal. 1999:117;1490.
- Ambartsumyan VA. Stellar masses. Ann Rev Astron Astrophys. 1980;18:13
- Sean RN. A review of graduate nurse transition programs in Australia. Icarus. 2006:183;265.
- Lynden-Bell D. Monthly notices of the Royal Astronomical Society.168;603:1974.
- Reipurth B, Bally J. Design of jet-driven, radiative-blast-wave experiments for 10 kJ class lasers. Ann Rev Astron Astrophys. 2001:39;403.
- Mirabel IF, Rodriguez LF. Sources of relativistic jets in the galaxy. ARA&A. 1999:37;409.
- Mґeszґaros P. The new galaxy: Signatures of its formation. ARA & A. 2002:40;137.
- Marscher AP, Jorstad SG, Gomez J, et al. Unexpected high brightness temperature 140 pc from the core in the jet of 3c120. Nature. 2002:417;625.
- Blandford RD. Active galactic nuclei. Courvoisier, Mayor TL, (eds) Saas-Fee Advanced Course 20 (Les Diablerets: Springer-Verlag) 1990;161-275.
- Scheuer PAG. Models of extragalactic radio sources with a continuous energy supply from a central object. MNRAS. 1974;166:513.
- Blandford RD. Hydromagnetic flows from accretion discs and the production of radio jets. Payne DG, MNRAS. 1982;199:883.
- Henriksen RN, Valls-Gabaud D. From Giotto to Rosetta – A collection from the ESLAB 50 Symposium. MNRAS. 1994;266:681.
- Meier DL, Koide S, Uchida Y. High energy density laboratory astrophysics. Science. 2001;291:84.
- Price DJ, Pringle JE, King AR. From Giotto to Rosetta – A collection from the ESLAB 50 Symposium. MNRAS. 2003;339:1223.
- Soker N, Regev O. arXiv:astro-ph/0305422v1 22 May 2003; Proceedings of the International Astronomical Union, 2007.
- Matveenko LI. Many-faced unity. IKI RAS. Pr-2179. Moscow. 2016.
- Abrahamyan MG. Vortical mechanism for generation of astrophysical jets. Astrophysics. 2008;51:163.
- Abrahamyan MG. Vortical mechanism for generation of astrophysical jets. Astrophysics. 2009;52:119.
- AbrahamyanMG, Matveenko LI. Vortical mechanism for generation of astrophysical jets. Astrophysics. 2012;55:397.
- Hernandez X, Rendґon PL, Rodrґıguez-Mota RG, et al. arXiv: 1103.0250v1 [astro-ph.HE], Proceedings of the International Astronomical Union, 2011.
- Ray T, Muxlow TWB, Axon DJ, et al. X-rays from jet-driving protostars and T Tauri stars. Nature. 1997;385:415.
- Getman KV, Feigelson ED, Townsley L, et al. X-ray emission near the substellar limit: The $\sigma$ orionis and taurus star forming regions. Ap. J. 575:354.
- Lautrup B. Physics of continuous matter (2nd ed.), CRC Press, 2011.
- Shakura NI, Sunyaev RA. Physics of continuous matter, (2nd ed.),: Exotic and Everyday Phenomena in the Macroscopic World. A&A. 1973;24:337.
- Shore SN. Astrophysical hydrodynamics, (2nd revised edition), Wilen, 2007, 468.
- Toomre A. Galactic spiral arms by swing amplification. Ap. J. 1964;139:1217.
- Balbus SA, Hawley JF. A powerful local shear instability in weakly magnetized disks. I - Linear Analysis. II - Nonlinear evolution. Ap. J. 1991;376:214.
- Rozyczka M, Spruit HC. A powerful local shear instability in weakly magnetized disks. I - Linear Analysis. II - Nonlinear evolution. Ap. J. 1993;417:677.

