Short communication

, Volume: 7( 1) DOI: 10.37532/2320-6756.2019.7(1).172

• View PDF
• Download PDF

Insight on the Emergence of Classicality from Quantum-Ness

*Correspondence:

Ghosh AK Ph.D. (Physics), Bhagwant University, India, E-Mail: ghosh.971@gmail.com

Abstract

Classical object has wave nature and wave-particle duality compounds confusion. On the contrary, quantum object is a coherent complex wave function which is probabilistic in nature. Classical and quantum interference differ by the presence of intermediate quantum interference terms which give rise to measurement problem. GRW theory, Pilot-wave formulation of quantum mechanics, Von Neumann, Zurek, Wheeler, Born’s principle, and also many physicists have worked on measurement problem. According to decoherence theory, quantum alternatives vanish due to the effect of entanglement with the environment. In this paper, I assume the effect of observer’s mind with respect to measuring device in order to explain classical behaviour from quantum-ness

Keywords

Quantum-ness; Decoherence theory; Transition

Introduction

Copenhagen interpretation said: there is common sense (classical) and there is quantum sense, but you can’t have both-at least, not at the same time.

Quantum processes are probabilistic and irreversible. They are different from classical measurements. Quantum theory explains the interactions between the object and the measurement apparatus. In classical physics, the observer registers the state of the real world without perturbing the observed system. But this cannot give a satisfactory answer to the basic question as regard to the constraints put on the results of physical measurements.

Quantum measurement has been discussed by J. von Neumann in his 1932 book and by decoherence phenomenon. The famous Solvay 1927 Congress and the 1983 review by Wheeler and Zurek thaught about measurement problem.

According to Born principle, the outcome of the measurement of an observable A on a state ψ is non-deterministic. Quantum mechanics give only probabilities and in particular the expectation value of the outcomes. This expectation value is given by the Born rule.

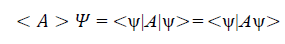
These measurements can be repeated and performed independently.

The probability to get the outcome 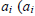being the eigenvalue of A and 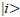the corresponding eigenvector) is the modulus squared of the probability amplitude i|ψ probability of outcome of A = ai in the state 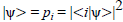[1].

It also indicates that quantum measurements are an irreversible process. In ideal measurements, this can be repeated. This is
the projection postulate.

According to the concept of hidden variables and “element of reality” the quantum state of a quantum system could be
explained by some hidden variables in some space. This idea was rejected by most physicist after 1927 Solvay Congress and
the advances of 1930.

According to the Von Neumann paradigm, an ideal measurement is an interaction between the quantum state (e.g. a q-bit )
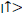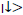and measurement apparatus. An ideal non-destructive measurement does not change the orthogonal states of and of a
quantum system. This is also a projection postulate, and hence this plays a crucial but controversial role. This means that this
postulate has a conflict with Schrödinger’s equation.

Thus, the ambiguity of quantum measurement has been a controversial problem for a long time [1].

In the context of classical and quantum interference, the probabilistic nature of wave function gives rise to various quantum
effects [2-4].

The probability of observing the system making the transition from state Ψ to the new state ɸ is given by

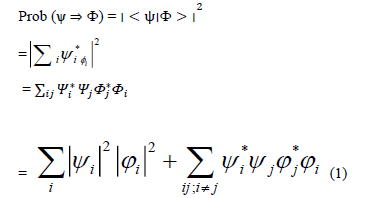
Where 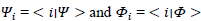are the coefficients of the final state of the system * is the complex conjugate so that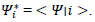

Now, if the system transit classically from 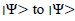via an intermediate state 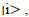then we get

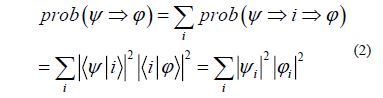
Therefore, from equations (1) and (2) we can see that quantum equation differ from the classical equation by the extra terms 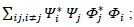these are the quantum alternative states [5-11].

According to decoherence theory, these alternatives vanish due to the effect of entanglement of the environment.

Conclusion

Let me present my imagination (where I have failed to make contact with standard quantum theory and the measurement axioms of quantum theory) is that the quantum alternative states are produced out of phase with each other in the plane of the observer’s mind with respect to the measuring device, and hence they are canceled out due to destructive interference among them and the single classical entity is left undisturbed. This might be a description as to how to get the single entity from quantum-ness.

References

1. Francios D. A short introduction to the quantum formalism[s]. Mathematical Physics. 2012.
2. Eibenberger S, Gerlich S, Arndt M, et al. Matter-wave interference with particles selected from a molecular library with masses exceeding 10000 amu. Phys Chem Chem Phys. 2013;15:14696-700.
3. Y Couder, E Fort. Probabilities and trajectories in a classical wave-particle duality. J Phys Conf Ser. 2012;361: 012001.
4. https://www.leica-microsystems.com/science-lab/phase-contrast/
5. WH Steel, Interferometry, second Edition: Cambridge Studies in Modern Optics 1, Cambridge University Press, Cambridge. 1986;4:319.
6. Pfleegor RL, Mandel L. Interference of independent photon beams. Phys Rev. 1967;159:1084-88.
7. Patel R, Achamfuo-Yeboah S, Light R, et al. Widefield two laser interferometry. Optics Express. 2014;22:27094-101.
8. Born M, Wolf E. Principles of Optics, Cambridge University Press, Cambridge. 1999.
9. Greene, Brian. The elegant universe: Superstrings, hidden dimensions, and the quest for the ultimate theory. New York: W.W. Norton. 1999:97-109.
10. Longhurst RS. Geometrical and physical Optics, Longmans, London. 1968.
11. Wojciech HZ. Decoherence and the transition from quantum to classical. Physics Today. 1991;44:36-44.