Mini Review

, Volume: 13( 1) DOI: 10.37532/2320-6756.2025.13(1).352

• View PDF
• Download PDF

Inhomogeneous Warm Electron Beam Interaction with Collisional Magnetized Inhomogeneous Warm Plasma

*Correspondence:

Kh. H. El-Shorbagy
Department of Plasma Physics and Nuclear Fusion, Division of Materials and Nuclear Industrialization, Nuclear Research Center, Egyptian Atomic Energy Authority, Cairo, Egypt
E-mail: drkhalede@yahoo.com

Abstract

In the presence of an external static magnetic field, we examine the linear interactions between an inhomogeneous collisional warm plasma and an inhomogeneous warm beam of electrons of arbitrary density. The dielectric of magnetized plasma remains unaffected by the inhomogeneity and warmth of the beam and plasma, which causes an amplification of the electric field. While the electric field amplification is influenced by both the external static magnetic field and the warmness of the beam-plasma, the dielectric constant remains unaffected. Additionally, it is discovered that the inhomogeneous electron beam affects the waves and in turn, the power that the plasma absorbs. Furthermore, a significant factor in the energy transmission between the beam and the plasma is the collision plasma term.

Keywords

Magnetized warm plasma instability; Inhomogeneity in EB-plasma system; Warmness of EB-plasma

Introduction

Applications for electron beams are numerous and include material research, compact torus construction, ion acceleration, ray and microwave generation, and other fields where long-term energy sources are desired. The employment of an electron beams to heat the plasma to a high temperature has garnered a lot of interest as a potential use, both experimentally [1-5] and theoretically [6-8].

The behavior of the growth rate as a function of the problem's parameters is typically studied for one or two oscillation modes that have the highest growth rates in beam-plasma instability treatments [9-13]. This method has provided significant insight into how the behavior of the beam-plasma interaction is influenced by the transverse transit of the oscillation energy and the group velocity out of the beam region [14].

These investigations, however, are unfinished and did not look into the impact of the electron beam-plasma interaction's nonhomogeneity.

Literature Review

Furthermore, to fully understand the spectrum of plasma waves stimulated by the inhomogeneous electron beam-plasma, it is crucial to analyze the linear stage of inhomogeneity beam-plasma instability. In this study, we examine the linear interaction between the external static magnetic field and the warm inhomogeneous electron beam-plasma system.

Researchers looked into how a static external magnetic field affected the linear interaction between a relativistic electron beam and an inhomogeneous, cold, bounded plasma [15,16]. This work studies the linear interaction [17,18] between inhomogeneous heated EB and inhomogeneous, colliding, warm magnetized plasma.

The field equations that characterize the system are second order differential equations. We solve the field equation using the following linear density formula.

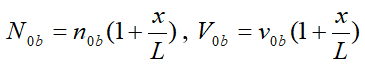
Where is the length scale of the variation ( L >> x ). The electric field of the interaction is calculated. Waves are excited more strongly in this case compared to inhomogeneous cold electron beam with unmagnetized cold plasma.

Fundamental waves

The first linearized set of equations (the equation of motion and the continuity equation) for 1-D electron beam oscillations are as follows:

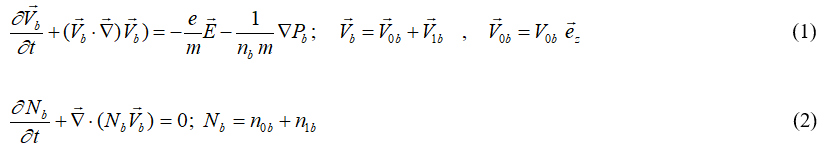
The initial linearized pair of equations (the equation of motion and the continuity equation) characterizing the oscillations in 1-D for inhomogeneous collision heated plasma electrons in the oscillating electric field are:

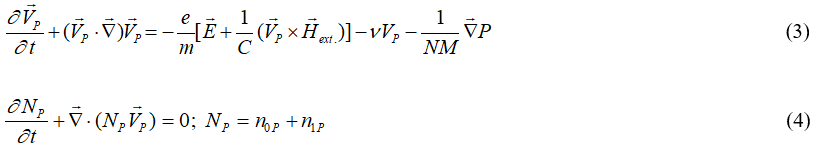
The unperturbed velocity and density of the beam are represented by V_ob and n_ob in equations (1-4), whereas the unperturbed and perturbed density of the plasma are represented by nop and n1p. v is the collision between electrons in the plasma and other plasma particles, as well as P_b and is the beam and plasma pressure. Every other phrase has its standard meaning.

From equations (1) and (2) we get for warm EB the following expressions:

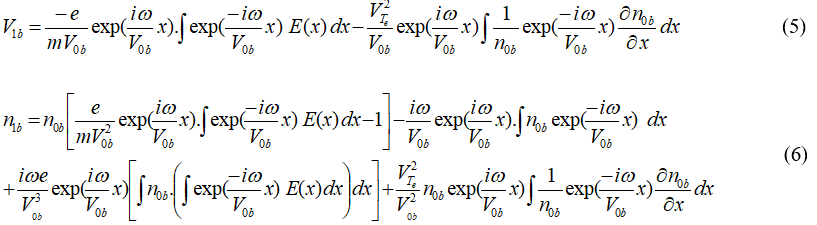
Where, V_Te=√kT_e/e is the electron thermal velocity.

Discussion

Similarly, from the continuity equation and equation of motion of the plasma, we can obtain the perturbed density of the plasma as follow:

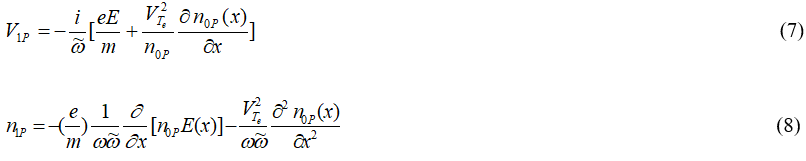
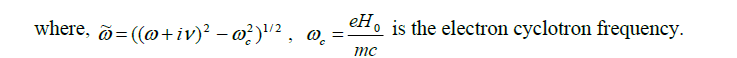
Using Poisson's equation

moreover, by substituting from (6) and (8) into (9) we have:

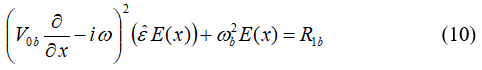
When v=0, N_b=const., V_ob=const., V_Tc=0 and H₀=0, i.e., the case of a homogeneous nonrelativistic electron beam with unmagnatized cold plasma, equation (10) becomes:

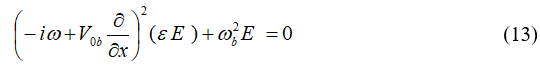
Equation (13) is in agreement with the work of MAH Khaled. Equation (10) can be solved in the region by the same method in Ref. Kh H El-Shorbagy to get;

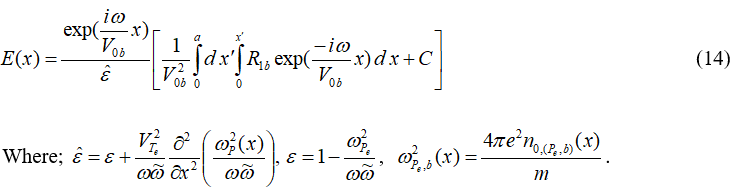
The dielectric ε(x) is not affected by warmness of the beam while the electric field amplification is affected by the warmness of the beam-plasma. In the case of a cold beam and cold unmagnified plasma v=0, N_b=const., V_ob=const., V_Te=0 and H₀=0⇒R_1b→R_b and εˆ→ε equation (13) is the same equation as reference.

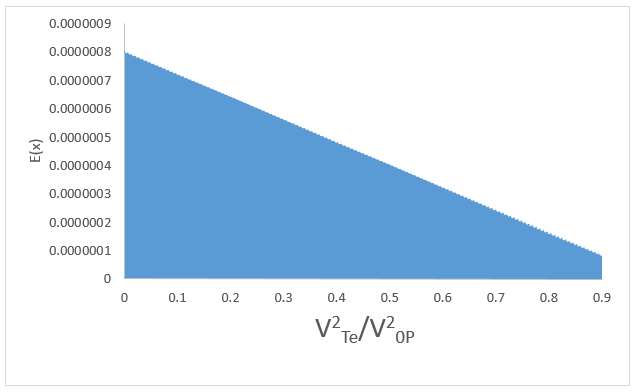
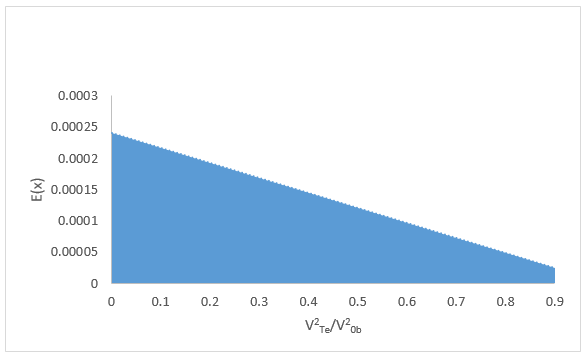
Plotting curve Figure 1, between electric field of wave and (V² _Te/V² _0P) in the case of interaction of warm beam and warm plasma and Figure 2, between electric field of wave and (V² _Te/V² _0P) in the case of interaction of warm beam and cold plasma, it is found that the warmness of the plasma decreases the electric field in compared with the case of warm beam and cold plasma.

FIG. 1. Electric field with (V² _Te/V² _0P) in the case of warm beam and warm plasma.

FIG. 2. Electric field with (V² _Te/V² _0b) in the case of warm beam and cold plasma.

Conclusion

In this paper, we study the interaction between magnetized warm plasma and an inhomogeneous warm beam. We are now able to look at how the inhomogeneity of the electron beam and the plasma can excite waves in the plasma. If we apply the differential equation we obtained to our instance, it agrees with the case of homogeneous beam-unmagntized plasma, and equation (13) is the same as ref. Equation (10) is found, which describes the system.

Equation (14) indicates an increase in the beam-plasma interaction's electric field. This indicates that there is less interaction between the beam and the plasma waves because of their local nature; in other words, the Chernkov resonance requirement (inhomogeneous density of beam and plasma) can only be satisfied locally due to the variable's dependency.

It is demonstrated that, depending on the density inhomogeneity of the beam and plasma, the beam-plasma interaction may significantly suppress the plasma. In contrast to the situation of an unmagnetized cold plasma, the presence of an external static magnetic field causes the electric field to grow. It is discovered that as the thermal velocity rises and the temperature of the heated electron beam rises after that, the electric field decreases.

Additionally, it is discovered that the inhomogeneous electron beam affects the waves and, in turn, the power that the plasma absorbs. Furthermore, a significant factor in the energy transmission between the beam and the plasma is the collision plasma term. Finally, compared to inhomogeneous electron beam-unmagnetized plasma, it is demonstrated that the growing rate of the instability in the former has decreased.

References

1. de Haan PH, Janssen GC, Hopman HJ, et al. Injection of a relativistic electron beam into neutral hydrogen gas. Phys Fluids. 1982;25(4):5.

   [Crossref] [Google Scholar]

2. Friedman M, Serlin V, Drobot A, et al. High-power modulated intense relativistic electron sources with applications to RF generation and controlled thermonuclear fusion. IEEE Trans Plasma Sci. 1986;14(3):201.

   [Crossref] [Google Scholar]

3. Zaki NG, El-Shorbagy KH. Electron beam interaction with an inhomogeneous warm plasma and wave radiation. Egypt J Phys. 1998;29.

   [Google Scholar]

4. El-Shorbagy KH, Sahyouni WM. Electron beam instability in an inhomogeneous warm plasma. Arab J Nucl Sci Appl. 1999;32(1):185-191.

   [Google Scholar]

5. Thode LE. Effect of electron?ion collisions on the nonlinear state of the relativistic two?stream instability. Phys Fluids. 1977;20(12):2121-2127.

   [Crossref] [Google Scholar]

6. Janssen GC, Granneman EH, Hopman HJ. Observation of high?frequency fields due to the interaction of a relativistic electron beam with a plasma. Phys Fluids. 1984;27(3):736-745.

   [Crossref] [Google Scholar]

7. Gupta GP, Vijayan T, Rohatgi VK. Relativistic electron beam heating of a hydrogen plasma in open confinement systems: Theoretical model. Phys Fluids. 1988;31(3):606-611.

   [Crossref] [Google Scholar]

8. Popkov NG. Method of eigenfunctions and noneigenfunctions in the theory of the beam-plasma instability of a spatially bounded electron beam. Sov J Exper Tech Phys Lett. 1984;39:255.

   [Google Scholar]

9. Kachalov KO, Popkov NG. To the nonlinear theory of interaction of a belt-like electron beam with an unbounded plasma. Fizika Plazmy. 1989;15(11):1310-1314.
10. Bilikmen S, Nazih RM. The nonlinear cold plasma-bunched beam interaction and the plasma wakefield accelerator case. Phys Scrip. 1993;47(2):204.

    [Google Scholar]

11. El-Shorbagy KH, El-Bendary AA, Mahassen H. Nonlinear interaction of the inhomogeneous electron beam with magnetized inhomogeneous cold plasma. Ind J Phys. 2022;96(1):289-292.

    [Crossref] [Google Scholar]

12. Malik HK, Singh S. Conditions and growth rate of Rayleigh instability in a hall thruster under the effect of ion temperature. Phys Rev E Stat Nonlin Soft Matter Phys. 2011;83(3):036406.

    [Crossref] [Google Scholar] [PubMed]

13. Singh S, Malik HK. Effects of initial ion velocity, magnetic field and plasma density profiles in simulating the plasma plume in a Hall thruster. J Astrophys Astron. 2023;44(1):3.

    [Crossref] [Google Scholar]

14. Singh S, Malik HK. Role of ionization and electron drift velocity profile to Rayleigh instability in a hall thruster plasma. J Appl Phys. 2012;112(1).

    [Crossref] [Google Scholar]

15. El-Shorbagy KH, Mahassen H. Long-wavelength oscillations in a REB interaction with cold plasma. Ind J Phys. 2022;96(14):4337-4340.

    [Crossref] [Google Scholar]

16. Khaled MA. Dust ion acoustic solitary waves and their multi-dimensional instability in a weakly relativistic adiabatic magnetized dusty plasma with two different types of adiabatic electrons. Indian J Phys. 2014;88:647-656.

    [Crossref] [Google Scholar]

17. El-Shorbagy KH, Swilem Y, Dakhel BM. Electron beam instability in magneto-active inhomogeneous cold plasma. Life Sci J. 2014;11(4):482-485.
18. El-Shorbagy KH, Shalaby SA, Mahassen H, et al. Interaction of inhomogeneous warm electron beam with collisional cold plasma. Ind J Phys. 2024;98(7):2579-2581.

    [Crossref] [Google Scholar]