Original Article

, Volume: 11( 6) DOI: 10.37532/2320-6756.2023.11(6).355

• View PDF
• Download PDF

Inertial Motions and Laplace Invariant

*Correspondence:

Yuriy Zevatskiy Independent Researcher, Ukraine E-mail: yuri@newchem.ru

Abstract

The dynamics of particle motion is investigated within the frame of a relativistic model, constituting an Euclidean space with three real spatial axes and one axis corresponding to the local (Eigen) time. An assumption is set forth about the isotropy of this tetrameric space at small velocities of the objects as a consequence of the equivalence principle of the spatial and Eigen time coordinates. The equations for trajectories are found, which are classified as the inertial motion. In the three-dimensional spatial basis, besides the trivial solutions, they include the accelerated motion in the harmonic and gravitational fields. In the latter case, such a motion can be implemented under the assumption of the two-dimensional nature (or complexity) of the Eigen time of the particles. The Laplace invariant is constituted by the real components of the coordinates and velocities.

Keywords

Relativistic model; Eigen time

Introduction

It has been known since long ago that the mass center of a body, left by itself, that is without acting forces, either stays in rest or moves uniformly along a straight line. If we consider not a single body, but a system of bodies, which are isolated from the external forces, the character of motion of the mass center of each of the bodies will not be changed, provided that there are no interactions between these bodies. It is of common knowledge that in this case anybody of the system moves along geodesic lines [1].

In the present work, we tried to find the solutions for the said isolated system with trajectories of the bodies, which differ from geodesic lines. Evidently, both classical mechanics and general relativity theory give a negative answer to this question [2-4]. Therefore, further consideration is based on the principles of the Special Relativity Theory (SRT).

Single Body Problem

The pseudo-Euclidean metrics conserves the interval of the Eigen (local) time of a particle τ with respect to any inertial frames of reference, in which it undergoes the displacements dx, dy, and dz in the time interval dt.

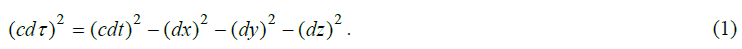
The invariance with respect to the Lorentz transformation is the basics for the construction of relativistic theories. The application of the principles of the Special Relativity Theory to the calculation of the gravitational potential has encountered certain difficulties in the interpretation of the results of astronomical observations [5]. Nevertheless, the works on the development of a relativistic theory of gravitation are challenging and still ongoing [6].

It was shown earlier that the relativistic kinematics allows reformulation in the tetrameric Euclidean space [7]. It is achieved by the replacement of the temporal coordinate t in the selected inertial frame of reference with a coordinate, corresponding to the Eigen time of the particles. Indeed, for any i-th particle the invariant (1) can be rewritten in the form,

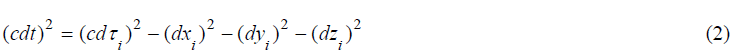
In the frame of reference, tied to the body, with respect to which certain particles are in rest, the lapse of their Eigen time corresponds to the lapse of time in the said frame of reference. Besides that, all particles undergo displacements, equal in the absolute value, which is the consequence of the equation (2),

Dot marks the differentiation over the natural parameter of the system ct. The interval of the Eigen time of the i-th particle cdτi is denoted as dwi. The world lines of the light rays are located on the hyperplanes, orthogonal to the axis of the Eigen time of a body, to which the frame of reference is tied. The world lines of the particles, immobile with respect to this body, are straight lines, parallel to the axis of its Eigen time. The principal relativistic equation relating the invariant mass m with the full energy and kinetic momentum of a particle can be obtained by multiplying l.h.s. and r.h.s. of (3) with m²c²ẃ ^-2

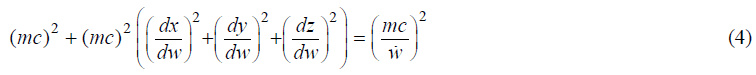
The principal assumption of the present research refers to the domain of small velocities of the particles or to the classical limit,

Subject to this proviso, the equivalence is supposed of the spatial coordinates and the coordinate of the eigen time. This assumption is set forth on the analogy of the Minkowski space where the time in the inertial frame of reference has an equal status with three spatial coordinates. Therefore, we assume the homogeneity of the space and eigen time with respect to the infinitesimal rotations of the coordinate axes (as a partial case of the Noeter theorem). This is manifested in the absence of the moments of forces, acting on the particles in this frame of reference, or under the condition (5),

where r is the coordinate with indices j or k, running from 0 to 3. Solving (6) together with (3) yields two types of the solutions. First type,

Corresponds to the motion along a straight (geodesic) line, and the second type,

Corresponds to the motion on the tetrameric sphere. Evidently, if the coordinate values are real, for the solution (8) to be implemented, it is necessary to make an assumption on the change of the sign of the eigen time of a particle w. Nevertheless, the fundamental equation (1) defines quadratic forms, which gives a certain freedom in the determination of the values themselves. The motion on the tetrameric sphere with radius R corresponds formally to the equation in the form,

where r is the tetrameric vector of the position of a particle (r0, r1, r2, r3) with respect to its center, and u is a linear antisymmetric operator with constant matrix elements, according to (6),

j is the number of a column, k is the number of a row.

The vector r is one of the Eigen vectors of the operator u². So, differentiating the equation (9), the transformation can be made to the form,

corresponding to the motion in the field of a harmonic potential. The solutions to the equation lie in one plane, hence the trajectories of the particle motion, according to the condition (8), are plain circles as the crossing lines of the hyperplane and tetrameric sphere. In the three-dimensional space, they correspond to ellipses or circles.

Let us represent (8) in the form,

Express w² from the equation of the tetrameric sphere,

and ẃ² from the normalization condition (3). After simple transformations, we get the expression for the square of the spatial mechanical momentum of a particle (integral of area), l(x,y,z)=r(x,y,z)v(x,y,z), conserving in this motion of the particle:

This result can be interpreted as follows. From the principles of the Special Relativity Theory, in the absence of external forces, the body can perform spontaneous oscillatory movement around an immobile point (center of mass).

The intrinsic angular momentum (spin) can be interpreted as a vector pro-duct containing the components of the eigen time of a particle w and coordinates in the space r(x,y,z), on one hand, and velocities by these coordinates ẃ and v(x,y,z). It can, like the spatial mechanical moment (14), have assume two opposite spatial directions.

Two-Body Problem

It is known that the harmonic and gravitation fields have a common integral-the Laplace invariant [8]. Therefore, it is of interest to elucidate whether the description proposed above can interpret the gravitational interaction without referring to the forces concept. Within the two bodies problem, elementary transformations of the Laplace invariant yield,

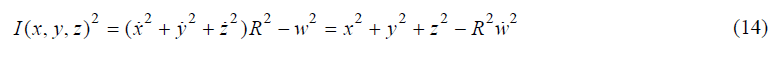
it is seen that it presents the components of the vector products of the coordinate r(w,x,y,z) and velocity ѓ(w,x,y,z) in the projection onto the plane spanned by vectors r(x,y,z) and v(x,y,z). In (15), α is the gravitational constant, ε is the eccentricity, the coordinate notations (x,y,z) for the velocity vector in the three-dimensional spatial basis v(x,y,z) are omitted.

Let us assume that the Eigen time is a complex value, and the Laplace integral (15) is formed by the real components of the Eigen time w_R and velocity ẃ_R up to a dimensional factor. In the particular case of the finite motion, the absolute value of the eccentricity is 0<ε<1, the Hamiltonian is H<0, and if this factor is equal to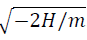, we get the following expression for the real Eigen time and velocity:

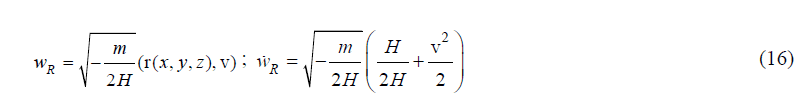
At these values, the motion of a particle is the rotation over the circle with radius R, formed by the crossing of the hyperplane and tetrameric sphere of the same radius. The following integral of motion is conserved,

with respect to one focus of the ellipse as the projection of this circle onto the three-dimensional spatial basis. The larger semi-axis of the ellipse is R, the modulus of eccentricity is ε, here and in what follows r(x,y,z) is the coordinate vector in this basis from the indicated focus to the particle.

This result can be interpreted as follows. Without the introduction of the interaction forces, a body in the presence of another body can perform a spontaneous finite movement in the three-dimensional spatial basis on the ellipse with one of the foci, located in the center of mass of the system. Another type of motion is implemented under the same conditions (3) and (8); the difference from the previous result for the spontaneous motion in the harmonic potential field (11) is in the symmetry violation due to the presence of the second body. The motion with the normalized velocity, according to (3), is implemented in the basis formed by the threedimensional space and the complex axis of the Eigen time-five independent coordinates in total. In the basis of the real coordinates, the motion is performed on the tetrameric sphere, according to the condition (8); new integrals of motion are conserved, which are generated by the infinitesimal rotations of equipollent coordinates not with respect to the center of this sphere. According to the normalization condition (3), the square of velocity of the imaginary component of the Eigen time is equal to,

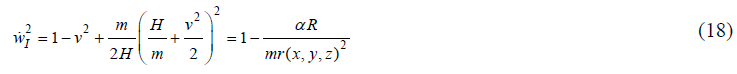
t is evident that the force of the observed gravitational field depends on the velocity v in the three-dimensional basis even for small subluminal velocities. The increase in the particle velocity at all other equal values (α, r(x,y,z), R) acts as the decrease of its mass m. This can provide an explanation of the accelerated recession of galaxies, which has been confirmed experimentally with confidence [9].

It is possible that the suggested relativistic model will find its application in respect to the problems of gravitation and "dark matter" [10, 11]. The experimental data that are referenced in evidence on the Euclidean nature of the three-dimensional space, which presents a strong argument in favor of the models with non-Riemannian metrics [10].

References

1. Gantmakher FR. Lectures in analytical mechanics. Mir Publishers; 1970.

   [Google Scholar] [Crossref]

2. Yu. G. Pavlenko, Lectures in Theoretical mechanics, Fizmatlit, Moscow. 2002:392.

   [Google Scholar] [Crossref]

3. Moller C. The Theory of Relativity, At the Clarendon Press, Oxford.1952:409.

   [Google Scholar] [Crossref]

4. Schild A. JL Synge, Relativity: The general theory., North-Holland Publishing Company, Amsterdam.1960:505.

   [Google Scholar] [Crossref]

5. T. Levi-Civita, E. Persico, Fondamenti di Meccanica Reativistica, NICOLA ZANICHELLI, Bologna, MCMXXVIII:185. [Google Scholar] [Crossref]
6. Logunov AA. Lektsii po teorii otnositel'nosti i gravitatsii. Sovremennyj analiz problemy (Lectures on relativity theory and gravitation). Lektsii po teorii otnositel'nosti i gravitatsii. Sovremennyj analiz problemy (Lectures on relativity theory and gravitation). AA Logunov. Nauka. 1987.

   [Google Scholar] [Crossref]

7. Zevatskiy Y. Inertial Motions and Laplace Invariant. Available at SSRN 4409941. 2023.

   [Google Scholar] [Crossref]

8. L.D. Landau, Е.М. Lifshitz, Mechanics : Volume 1, Elsevier Science, Burlington.1982:199. [Google Scholar] [Crossref]
9. S. Perlmutter. Regular and Singular Solutions Within Relativistic Gravitation Theory With Logunov Relations. Phys. Usp. 2013;56(10) [Google Scholar] [Crossref]
10. Lukash VN, Rubakov VA. Dark energy: myths and reality. Physics-Uspekhi. 2008 Mar;51(3):283.

    [Google Scholar] [Crossref]

11. Chernin AD. Dark energy and universal antigravitation. Physics-Uspekhi. 2008;51(3):253.

    [Google Scholar] [Crossref]