Review

, Volume: 6( 3)

• View PDF
• Download PDF

Generation and Annihilation of Energy Systems

*Correspondence:

Gudrun Kalmbach HE , Mathematic Informatics Naturewissenchaften, Technic, Germany, Tel: +49 (0) 30 25418-499; E- Mail: mint-01@maxi-dsl.de

Abstract

In physics, generation and annihilation is used for different processes. Annihilation mainly uses the energy of colliding systems to distribute the accepted energy newly. For instance, an electron colliding with an antineutrino can produce a W- boson carrying the common energy. The W- decay is then again into two particles. The article refers to known datas from physics, but is mostly from the book and many related articles of the same author. Involved are new symmetries or Gleason operators and different kinds of geometries. All sections of this article, not only the first one, are original research using. From physics for instance the early development of the universe is quoted, but physics has no explanation for this. The authors new method has for it detailed information, using matrix theory in form of Moebius transformations octonian projective and other (Hopf in section 2) geometries and Gleason measures with octonian spin-like GF triples (third section). The explanation of figures is kept short and the extended theory is found in the authors book and older publications not quoted here.

Keywords

Collision; Inversion; Generation; Gleason measures; Deuteron

Collision on Universe Scale

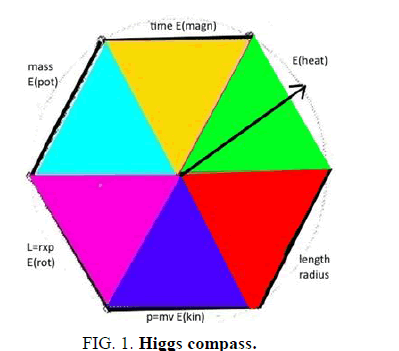
An example is the collosion of two galaxies. It is assumed that three vectorial energies or spacetime vectors are annihilated and for the new energy distribution a Higgs compass acts. Annihilated are a radius vector for space, a time vector and heat. Using the calculus of Gleason operators from [1], this means that a projection happens from a complex 3-dimensional space to a real 3-dimensional space. It is the GF space with probability distribution 0 for length, time and heat. The GF Gleason frame of this operator is a pairwise orthogonal triple like the spin coordinates but carries instead of the length of a spin coordinate sx, sy, sz other energies. In the new case it is a vector having an energy weight for mass, for kinetic energy as momentum and for anular momentum as rotational energy. The Higgs compass adds to them three color charges of the strong interaction SI turquoise rbar, blue, magenta greenbar. The needle of the compass is moving such that the color charge is located on an area between the first three sixth' roots locations of the needle. As generation or creation matrix the conjugation operator C of physics sets the conjugate color charges on the remaining three sectors of the circular compass by adding an angle of π. (FIG. 1.)

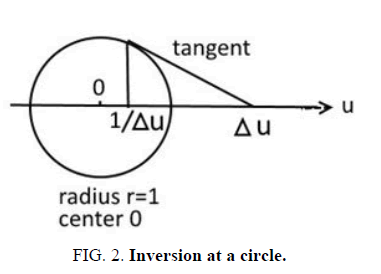
In the development of the early universe physics quotes as first items a Planck length interval, color charge red in the compass figure, a Planck time as interval color charge yellow and a big heat color charge green. The three color charge inversions by C combine then the interval measured and energies in form of the three Heisenberg uncertainites. In vector and matrix form the inversion uses the first Pauli matrix σ1, listed here as complex fraction 1/z for the associated coefficient matrix. Geometrically this can be described by the inversion at a circle (FIG. 2.).

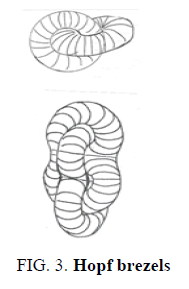
In the vectorial case, 1/r, a potntial for mass, is inverted by multiplication with σ1 to a length measured as radius r, a frequency as 1/Δt is inverted to a time quant Δt. In the third case the relation between angular momentum and heat is different. Of use are their associated matrices in the triangle symmetry D3 belonging to a nucleons quark triangle. As complex fractions they are (z-1)/z and z/(z-1). Multiplication of coefficient matrices from σ1 with one of these matrices gives the other one as inversion. In this case the numerical scaling is from a huge rotational speed at the collision to a extermely high heat. In differentials it is reminded that for heat replaced by an angles differential dφ for angular momentum L the matrix (not vector) inversion replaces it as time derivative by angular speed ω=dφ/dt for L=J ω. This can also be applied to a big bang situation for the universe. In the universe case two or three extremely huge energy systems replacing galaxies colloid (FIG. 3.).

Generation of Particles Size

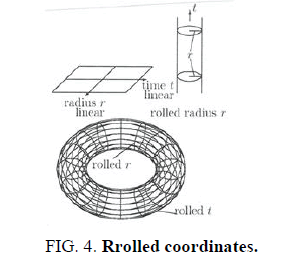
Taking for the known particle series the weak bosons as intermediate energy carriers after two particles colloid: their splitting into two generated particles according to the Feynman diagrams has the Hopf geometry of the Hopf sphere S³. It belongs to the SU(2) symmetry of the weak interaction WI. The Heegard decompositions of S³ allow the splitting into two brezels. Of use are tori of genus 1 and genus two brezels for quarks. In the upper torus decomposition the weak boson splits for instance into an electron and antineutrino or into a positron and a neutrino. The torus geometry can be changed. For neutral leptons the spindle torus is used with an axis carrying its spin plus momentum vector (helicity). If two photons are generated the torus is transversally cut along a circle to a cylinder. One toroidal period of the torus function is opened and photons have only one period for their functional description (FIG. 4.).

Rolled coordinates are generated by periods in a cylindrical strip or a rectangle in a plane. In these cases the inversion at a circle through the conjugation opertor C and σ1 is replaced by a weak boson as intermediate energy carrier after a collision of particles.

Gleason Frame Triples

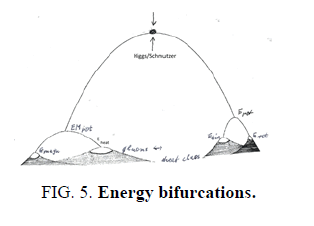
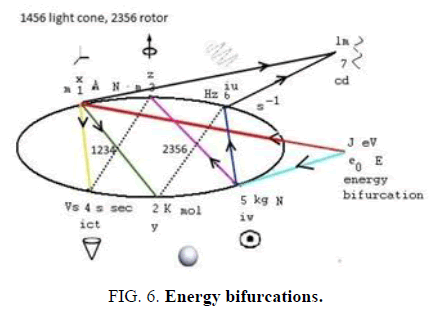
The explanation for a big bang can be expanded to Gleason frame GF triples like the three spin coordinates. Instead of spin vector coordinates length three arbitrary real weights 0<wj are added with a common weight w=Σwj for the associated Gleason measure. One weight can also be 0. (FIG. 5 and 6)

As in the first section GF vectors can be chosen for E(pot), E(kin), E(rot) as GFn and a Higgs compass together with the conjugation vector generats a new GFu with vectors for r, Δt and heat as entropy in a volume or as phonons. The weight of the Gfu can approach the probabilistic 0 space for its Gleason measure support (see [1]). A generated 5-dimensional Schmutzer field or Higgs (octonian e0) allows then the Feigenbaum bifurcation where the left branch in the bifurcation figure evolves newly through inversions. The 8 gluon/SI generation bifurcates in the last line. Then heat chaos occurs. In the Pascal ellipse figure at right also an octonian e0 as input vector is shown. The possible octonian photon 7 output from the electrons on shells of atoms is also drawn and evolves much later than atomic kernels.

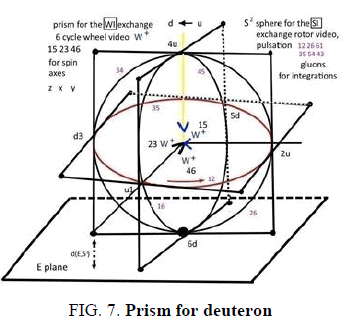
In this GFu evolution of the big bang first quarks are generated. After that, when neutral leptons can escape, nucleons and deuteron as time crystals are generated. In [2] they are described in the prism figure as follows. The Gfu sets three quarks barycenters as vertices of a nucleon triangle on a sphere S², using an edge length in three sizes ½, 1, 2. On the edges 12, 16, 26 or 34,35,45, are marked gluon exchanges which keep the quarks confined inside a nucleon. The dynamics for the time crystal is the symmetry of the quark triangle D3. It rotates a vector triple for Gfn whose vectors are now attached to the quark vertices in the figure SI rotor. At the vertices another Gfg is attached as endpoints of the rgb-graviton whirl GR which stretches or squeezes the nucleon triangle in three sizes (figure pulsation), called a POT motor for potentials. The time cycle is in six intervals from a matrix G of order 6 description of the compass. As complex coefficient matrix G arises from the scaled general relativistic factor (r-1)/r (radius r). The spin Gfs is generated by a weak rotor as wheel. Two oppositely oriented (on a diameter) located tangential vectors to a circle rotate in the xy- or xz- ot yz-plane and generate a spin vector on the rotation axis z or y or x. (FIG. 7.)

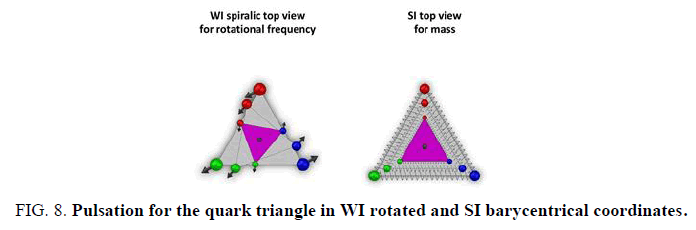
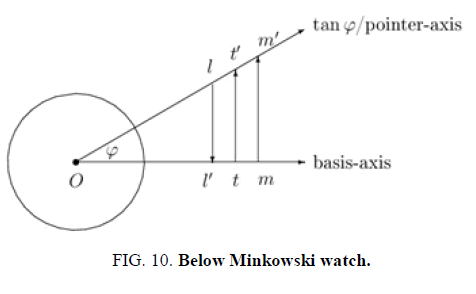
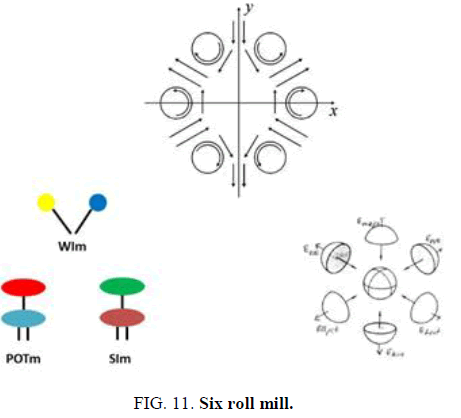
The weak W+ exchange in the prism is for this 46, 23 or 15 from a u-quark to an d-quark whose isospins are changing. The generated Euclidean coordinates of WI are in special relativistic SR motion towards the combined spherical SI and rgb-gravitons barycentrical coordinates. Gfg can replace at its r,g,b vector endpoints color charges by the three masses of the quarks. The Minkowski watch rescaling of mass is also for the other SR rescaling and generates the Minkowski metric for spacetime. The SR speed is coming from measuring the u-quarks mass wj for instance in the Euclidean WI coordinate vectors while the common weight w of the nucleon is measured in the SI/barycentrical coordinates. The turning angle φ between the two mass coordinates determines the SR speed v in an orthogonal projection scaling with cos φ, sin φ = v/c. This way the deuteron time crystal carries as well the general as the special relativistic actions which add up to the whole Einstein relativistic universe. It is driven by three motors POT, SI and WI as in the six roll mill. For the extended coordinates view it is useful to use octonians with coordinates named 0,1,...,7 where 1234 is for spacetime (4 is time), 5 is for mass and gravitational potential E(pot), 6 for frequency E(kin), 7 as a rolled circular U(1) Kaluza-Klein coordinate for lights cylindrical coordinates and exponential functions and 0 for the compass and its needle. Energy vectors or numbers are also added to 1 as EM(pot) electrical potential, 2 E(heat), 3 E(rot) rotation energy, 4 magnetic momentum or energy E(magn). (FIG. 8-11) below: the Heisenberg uncertainty couplings of rolls with added color charges and last figure: their location as hedgehog caps on a deuteron spherical ball surface for the energy exchange of its inner energies with the environment Unit spheres are the geometry of normed 1 quadrics in a real or complex metrical (n+1)-dimensional space. For a deuterons time crystal moving on its world line in an environment such quadrics are in use. Also Moebius transformations, GFs and central projections from projective geometry contribute to this.

1. Generated quark brezels (figure Hopf geometry) have two poles for S0 = {1,-1} on a real line. In a big bang collision the Pauli matrix σ1 inverts potential 1/Δx to the distance Δx between the two quark poles as a (Planck size) distance measure. The eigenvalues of σ1 are S0 with the metrical quadric x² =1.

2. Generated nucleons as quark triangle (figure pulsation) extends the former quadric to a circumference circle S1 of the triangle with metrical quadric x²+y² = 1 in a real plane. As inversion of frequency E(kin) in E = hf, h the Planck constant, E energy, a small time unit Δt is using the normed general relativistic scaling matrix G of order 6 (figure Higgs compass with six color charges) for the SI rotor (videos rotor, 12 roll mill with gluon SI exchange between paired quarks, GR pulsation, membran oscillation are available). The color charge blue vector E(kin) sets in rotation the three quarks barycenters as vertices of the triangle. Barycentrical coordinates are generated. The multivalued complex cross ratio sets with permuting four numbers 0,1,∞,z (a variable complex number) the triangle symmetry D3.

3. Generating deuterons uses the weak exchange between paired u-,d-quarks as in the Heisenberg uncertainties (video wheel). The weak SU(2) symmetry with the Pauli matrices generate by the wheel rotation the S² metrical quadric x²+y²+z² =1 in the real space R³ and the Hopf geometry S³, The E(rot) with symmetry α²εD3 inversion to entropy E(heat) with a boundary S² for its volume is inverted to the heat matrix σ1•α² = α•σ1εD3 .

4. Generating a world line on which deuteron moves in its environment uses the Hopf blow up to spacetime coordinates provided with Minkowski metrical quadric x² +y² +z² -c² t² , c speed of light (figure Minkowski watch). The SR rescaling of mass from m' to m for u-quark measured in WI coordinates and the GF common weight of quarks in a nucleon measured in SI coordinates has as SR speed v or -v between these two coordinate systems the normed matrix G•σ1. The mass rescaling is with m' = m/cos φ, sin φ = v/c. A GF can be from the id,α,α² εD3 triple of order 3, used for the vector SI rotation of E(pot), E(kin), E(rot).

5. General relativistic rescaling of Minowski matric is done by a central projection pr in projective, homogeneous coordinates and the scaled G matrix as fraction cos²β = (r-Rs)/r, sin²β = Rs/r, Rs the Schwarzschild radius of a central system (sun or barycenter) Q. The pr coordinates are (…,(r-Rs),...,r,...) and projective norming is with r. The oriented vector (length) distances are from Q to a rotating system P (about Q) |QP| = r and reversely |PQ| = r-Rs. It generates an accelerating force on the needle from Q to P such that this needle covers in time a larger area as required by the Kepler ellipse orbit of P. This means for the Einstein rosette as orbit of P that a fixed angle is added where P gets its nearest point towards Q after one revolution [3-7].

References

1. Kalmbach GHE, MINT-WIGRIS, MINT Verlag, Bad Woerishofen, 2017, available under: https://www.scholars-press.com
2. Book editions, vol. 1-38, 1997-2018, - the Deutsche Nationalbibliothek Frankfurt/M.
3. Kalmbach GHE. Deuteron States. Nessa J Phys. 2017;1:1-17.
4. Poston T, Stewart I. Catastrophe theory and its applications. Courier Corporation. 2014.
5. Gudrun Kalmbach HE. Field Quantum?s for Deuteron States. Biomed J Sci & Tech Res: 2018; 7:1-5.
6. Internet video under YouTube: Moebius Transformations Revealed 2014.
7. MINT, PF 1533, D-86818 Bad Woerishofen. Germany.