Review

, Volume: 7( 3) DOI: 10.37532/2320-6756.2019.7(3).183

• View PDF
• Download PDF

Disruptive Gravity: An Alternative to General Relativity

*Correspondence:

RB Safo
CentraleSupelec, France, E-Mail: ramses.bounkeusafo@gmail.com

Abstract

Viewing gravity as a space-time bending force instead of just a space-time curvature, we come to the conclusion of rest mass relativity. A close analysis of Schwarzschild's metric lead us naturally to the Vacuum Apparent Energy Invariance principle from which we derive the metric equation. Using quantum physics in a curved space-time study, we derive a coherent quantum equation that includes gravity. Applying this theory to cosmology, we can explain galaxies redshift as a delayed gravitational redshift which fully explains Hubble diagrams, including Dark Energy.

Keywords

Quantum gravity, General relativity, Dark energy, MOND theories

Introduction

Gravity is currently understood as a space-time curvature. We will first see how gravity can be seen as a force able to bend space-time instead and then derive a new space-time bending equation thanks to a new principle equivalent to Einstein’s Equivalence Principle in low-intensity fields.

In this paper, Greek letters range from 0 to 3 (representing space-time) while roman letters range from 1 to 3 (representing space), contravariant coordinates have low indices except for four-potentials and the metric signature is 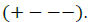We use Einstein’s summation convention.

A space-time bending force

Einstein’s General Relativity states that a body moving through gravity is just following the shortest path in curved space-time. This is summarized by the geodesic equations where the metric 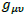is derived from Einstein’s equation. Those equations are derived from the least action principle, with the following Lagrangian:

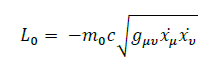
If gravity were a force, the Lagrangian would be of the form:

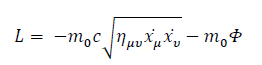
where 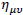is Minkowsky's metric and 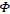is the gravitational potential.

We know this Lagrangian is not correct since it would lead to incorrect geodesic equations.

How could we get to the same geodesic equations as General Relativity taking into account space-time curvature and a potential term? Let the Lagrangian be of the form:

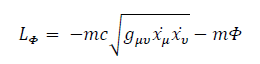
As such, we still wouldn't get the same geodesic equations as General Relativity. Is it possible to slightly change it in a physically acceptable way so it becomes equivalent to General Relativity's Lagrangian?

Speed of light cannot be modified since Special Relativity laws wouldn’t apply anymore. The only thing that could be changed is the mass of the body.

Let’s then write:

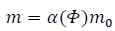
where m₀ is the rest mass in case of zero potential. So we have: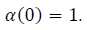

For more clarity, let's also write: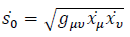

We then have: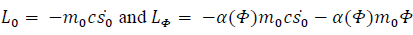

We want to find the same geodesic equations with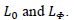

For General Relativity, we have:

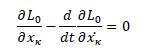
For our new Lagrangian, we have:

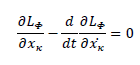
Since 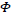doesn't depend explicitly on 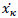we have:

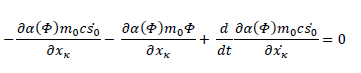
Leading to:

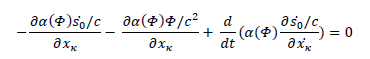
It comes:

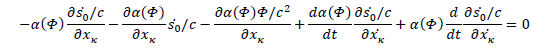
We see the Lagrangian equation of L₀ in the first and last terms of the equation:

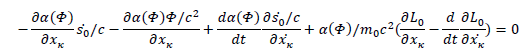
So we have the same geodesic equations as in General Relativity if and only if:

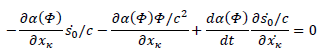
Parametrizing with the body's proper time, we have: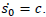

It comes:

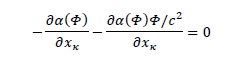
Thus:

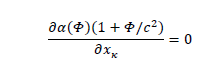
Eventually:

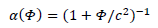
Gravity is then a space-time bending force if and only if the mass is relative such that:

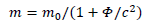
This is exactly what we wanted. Interpreting gravity as a force able to bend space-time instead of just a space-time curvature.

Mass changes seem to falsify the conservation of energy. For it to remain true, the energy has to be written as:

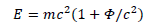
We generalize this formula as such for a relativistic body:

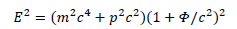
With: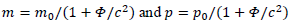

We are now left with finding how gravity could bend space-time. What physical principle could explain that? Can we derive the metric through a new principle other than General Relativity strong equivalence principle?

Metric Field

Let’s postulate that the metric is of the form:

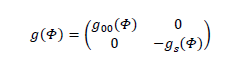
Where time dilation and spatial curvature are disjoint. Then would be a dependent function and g_swould be the spatial part of the matrix.

In this view, space-time is not bent by matter, but rather by gravitational potential.

Let’s derive 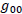and 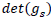first.

Time Dilation

Let’s derive 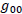with two different methods.

We introduce the Apparent Energy as such:

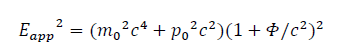
Thus:

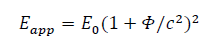
The apparent energy is the particle's energy under potential gravity as seen by an observer.

Applied to photons, we have: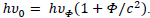

Thus: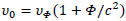

which is similar to a gravitational redshift.

From Einstein's gravitational redshift analysis, we have: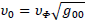

It comes: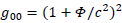

Let’s have a quick look at Schwarzschild’s metric:

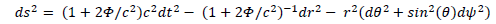
We have: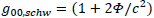

The difference is really small: 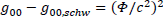but still noticeable. Precise measurement of gravitational redshift would decide which time dilation factor is the most accurate. This theory could be falsified this way.

Let's now see what g₀₀ comparing General Relativity's Lagrangian to a classic lagrangian. That would help us chose between Schwarzschild's result and ours.

The classic lagrangian is:

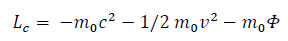
And let's rewrite General Relativity's lagrangian this way:

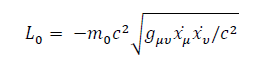
Then, for non-relativistic speeds, we have:

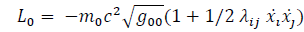
with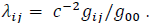

Equating both lagrangians, it comes:

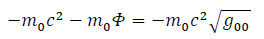
And eventually: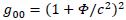

Schwarzschild's solution would be a first-order approximation while ours seems more precise. But since Schwarzschild's solution is an exact solution of Einstein's equation, if the real physically observed time dilation factor was mathematically different from Schwarzschild's, it would mean that General Relativity's equations are false. There should be a more accurate theory. Since General Relativity derives from the strong equivalence principle only, we should conclude that the strong equivalence principle is false. Therefore, one would rather find a new physical principle to build a new theory upon. Which is the aim of the next section.

Will also see a third way to derive g₀₀ applying a new principle which doesn’t depend on quantum physics in the next section

Vacuum Apparent Energy Invariance

We naturally want to change Schwarzschild’s metric into the following metric:

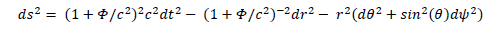
This way, in Cartesian coordinates, we would have:

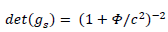
What could be the physical meaning of this? Let 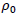be a mass density:

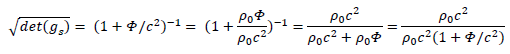
It’s just as if it was the ratio of the apparent energy of virtual vacuum masses under zero gravity potential over the apparent energy of those same masses under 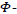potential gravity.

For an infinitely small space volume =dxdydz, we can write:

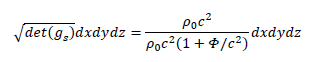
It comes:

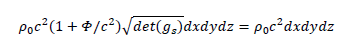
So we naturally introduce the Vacuum Apparent Energy Invariance principle (VAEI) as follows:

"The apparent energy of the vacuum is invariant."

Let's apply this principle to derive 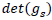and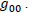

At a given point in time t, in an infinitely small volume 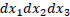under zero gravity (flat space) with vacuum energy density 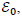we have:

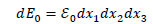
and under 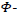gravity potential, we have:

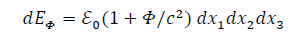
Applying VAEI, we have: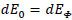

It comes:

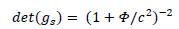
Let’s apply VAEI in the time domain to have a more rigorous way to find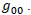

The reasoning is a bit similar to the one for the derivation of the gravitational redshift. We reason in terms of observational events.

Let E₀be the total vacuum energy and N be the number of observational events.

The apparent total vacuum energy by time unit for an observer under a global 0-potential is:

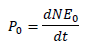
The apparent total vacuum energy by time unit for the same observer under a global Φ-potential is:

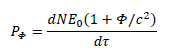
Applying VAEI, we have: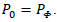

It comes:

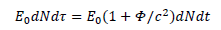
With 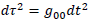it eventually comes:

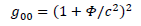
We don’t need a quantum argument anymore which is really important for this theory not to be dependent on quantum physics and the energy conservation argument wasn’t strong enough since gravitational redshift of photons implying a violation of energy conservation is currently interpreted otherwise.

Space Metric

We still don’t fully know g_s. We only know its determinant.

Spherical potential from a point like mass is a special case in which space is only dilated radially. Which gives locally in 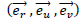basis:

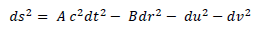
Applying the VAEI principle, it comes:

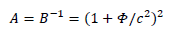
In this coordinate system, the spatial part of the metric is local:

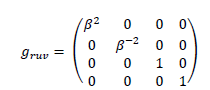
with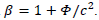

Changing coordinates, we get:

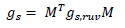
where M^T is the change of basis matrix from 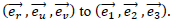So with 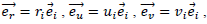we have:

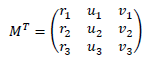
then:

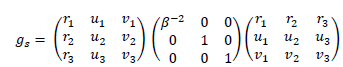
It comes:

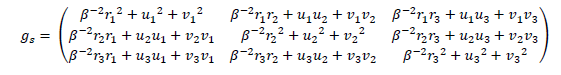
And using orthogonal matrices properties:

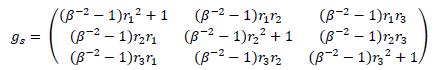
Eventually:

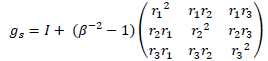
That doesn't depend on the choice of 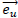and 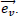It can be rewritten this way, with 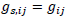for brevity:

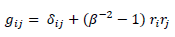
Which is only true for a spherical potential from a point like mass. How can we generalize it to any kind of potential?

The above formula is also locally true for a linear mass distribution along 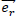passing through the observer's location in space.

Let:

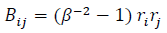
Let's rewrite the formula this way:

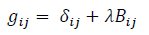
This way, λ is a renormalization parameter ensuring that 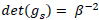while conserving the basis change invariance. In this special case, we obviously have λ = 1.

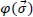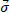If we are in presence of mass distribution, we want to add up the potential influence from every direction to derive g_s. We then introduce the angular potential distribution where is the observed direction. We have:

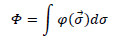
where 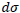is a solid angle element.

For an infinitely small solid angle in 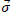direction, applying the previously derived formula, with 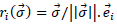we have:

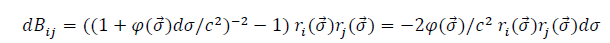
Integrating over the whole observation sphere we have:

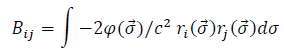
It eventually comes:

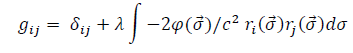
This metric solution is easily verified in the case of a point-like mass distribution. In the case of a homogeneous and isotropic mass distribution cross-terms are null so we have:

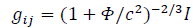
In case of a Newtonian potential in a static mass distribution no need for solid angles formalism. Adding up the potential influence from every mass, with 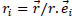for brevity, we have:

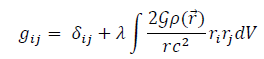
Gravitational Field Tensor

Gravitation seen as a force is very similar to electromagnetism. A direct analogy gives us the gravitational potential as a Lorentzian vector:

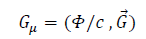
And the gravitational tensor as:

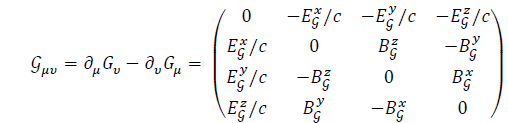
The lagrangian becomes:

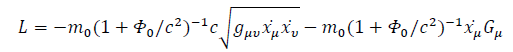
Where we now separate the vacuum potential 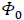from the particle’s gravitational potential. Einstein’s statement of equality of inertial and gravitational mass is not necessary anymore. And the potential is not necessarily a Newtonian one analogous to electromagnetism, leaving open doors to modified Newtonian gravity laws. If it was, we would have the equivalent of Maxwell equations for gravity. The last thing, gravitational waves are not dependent on a gauge choice contrary to General Relativity since the potential is Lorentzian by definition.

Electromagnetism

Any potential could be added to the Lagrangian, so including electromagnetism is pretty straightforward.

Let 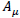be the electromagnetic four-potential. Including electromagnetism contribution to the Lagrangian, we have:

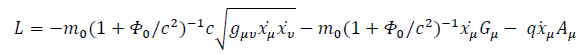
We see that the stronger the gravity field, the lesser the influence of other forces. Other forces can be neglected if gravity is strong enough.

Quantum Gravity

Gravity being a force again, we now have a coherent way to blend gravity into the quantum realm. What follows is based on Fock's equation (V. Fock, Z. Phys. 57, 261 (1929)) as a curved space-time version of Dirac equation:

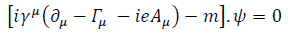
Were 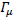are the generalized gamma matrices defining the covariant Clifford algebra (H. Tetrode, Z. Phys. 50, 336 (1928))

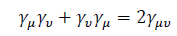
were 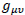is the space-time metric, whose signature is 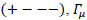is the spinorial affine connection and 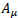is the electromagnetic four-vector potential.

In order to take into account gravity, we just write 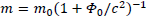and we take into account the gravitational four-vector potential 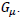We get:

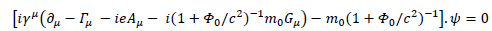
This way, we finally have a coherent quantum gravity equation! It only concerns 1/2-spin charged particles though. Same work should be done for quantum electrodynamics and quantum field theory in general.

Cosmology

Let's see how global vacuum gravitational potential evolves in a homogeneous and isotropic universe. The potential is induced by the mass in a ct radius sphere where is the age of the universe. Space dilation can be neglected in weak field approximation. We have:

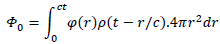
Where 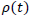is the universe matter density at time t and 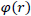is the potential of the gravitational field by the mass unit at a distance r. In the special case of Newton's law, it would be 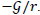Time dilation is neglected in the integral in weak field approximation and 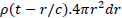is obviously not dependent on space dilation.

Let 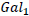and 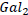be two galaxies at a distance D away from each other. An observer in 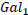at time t₀ would see 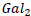as it was in the past at the time 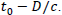The gravitational potential of 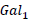and the gravitational potential of 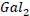at the time it's being observed are then:

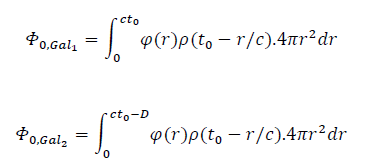
With the time dilation factor the observed redshifted frequency is:

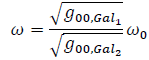
It comes:

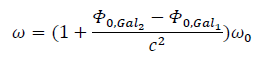
Thus:

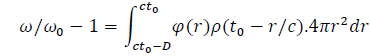
And eventually:

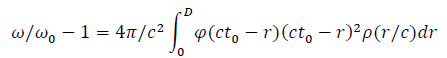
One could integrate and have the exact solution but it's easier to compare the distance derivative of the redshift to the observational data. We have:

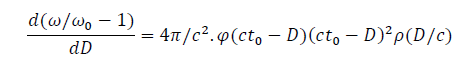
For very small distances, observational data show that 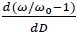is constant (Hubble law). Given that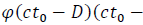 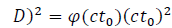in that case, 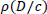must be constant. If 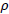evolved in the early universe, it must have been in time no greater than the time light would take to reach the nearest galaxies.

Let's write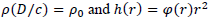

For small distances compared to the size of the universe, we have:

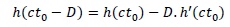
It comes:

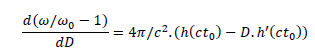
Eventually:

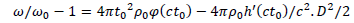
This is equivalent to Hubble's law with an acceleration term. From Hubble diagrams, we deduce 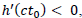which is verified for a Newtonian potential.

That gives a good explanation of Hubble diagrams with no need for any kind of Dark Energy.

Redshift is related to Hubble's constant as follows:

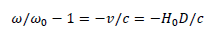
Identifying it to our formula, we have:

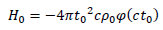
If we could measure redshifts in smaller distances, we would be able to have more accurate information about 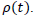A way to do so would be sending a signal and making it bounce back to were it has previously been emitted. The global gravitational potential will have changed and redshifted the signal [1].

Let 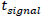be the time for the signal to come back. Doing the same reasoning as previously done in the case of galaxies, we have:

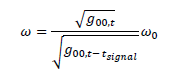
It comes:

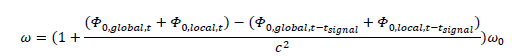
Since the local potential is not time-dependent, we have:

So we just have to replace D by 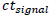in the previous equations:

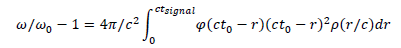
It comes:

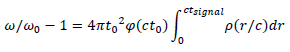
In other words after a variable change:

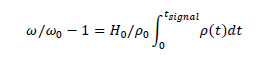
Plotting 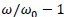against t_signal we can derive 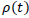as:

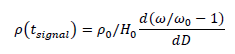
It's quite wonderful that there is a theoretical way to ''see'' the early stages of the creation of the universe.

Using the average mass density of the early universe, we can rewrite the redshift this way:

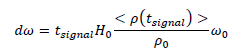
This could possibly be detected through laser interference modulation using a large interferometer. The path difference 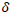and 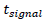are directly related: 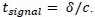One can then choose 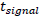to have constructive interences such as:

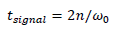
This is to better see the modulation phenomenon. Let's assume that 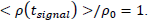It's possible to have laser frequencies of about 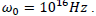Hubble constant is approximately 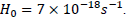With a length of about 3 km for the interferometer, we can have a maximum difference path of 6 km thus 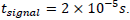That gives us:

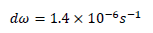
It's about 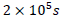oscillating period. It's roughly 8 days only! The longer the oscillating period, the lesser the average universe mass density before 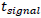[2].

Conclusion

This theory can be proven less accurate than General Relativity by fine measurements of the gravitational redshift. It could either falsify this theory or falsify General Relativity.

We never mentioned the Quantum Vacuum. This theory could have been created without knowing the existence of Quantum Vacuum, thus predicting its very existence. Quantum Vacuum being neutral, an electric field wouldn't induce any potential energy since negative and positive charges would nullify their potential energy. Quantum Vacuum being isotropic, its potential vector is null, justifying the fact that we only took into account the scalar potential throughout the whole paper.

Magnetic fields could change Quantum Vacuum energy since particles spins would tend to line up with field lines and thus have negative potential energy.

This theory is compatible with any violation of the weak equivalence principle and any non-newtonian gravity potentials.
The last important thing to mention is the retraction of the metric on the potential. Space dilation implies a modification of the way the potential is derived which in turn implies a modification of the space dilation until a balance is found. The maths of this effect can be done in the case of a spherical potential leading to really interesting discussions which are off topic.

The last section about cosmology is quite disruptive. Contrary to Einstein's equations, our theory doesn't imply an expanding universe but can predict what we observe and interpret as being an expansion as it also gives a natural explanation to what we interpret as Dark Energy. This theory says nothing about the very early moments of the universe though. But as you saw at the end of the last section, we have a powerful way to investigate these moments through what one may call Signal Bouncing Gravitational Redshift.

As you can imagine, there is a lot more to say about this. It implies many things about the nature of Quantum Vacuum, of gravity, or even of time itself but this is not the topic of this paper. The topic was to show how to interpret gravity as a force turning its quantization into a trivial thing given all the previously done research about quantum physics in curved space-time.

References

1. Fock V. Geometrization of the Dirac theory of electrons. Zeit F Phys. 1929;57:261-77.
2. Tetrode H. Allgemein-relativistische Quantentheorie des Elektrons. Zeit F Phys. 1928;50:336-46.