Conformally Flat, Quasi-Circular Numerical Simulations of the Chirp from Binary Neutron-Star Merger GW170817

G. J. Mathews; I.-S. Suh; N. Q. Lan; A. Kedia

doi:10.37532/2320–6756.2021.9(1).204

Review

, Volume: 9( 1) DOI: 10.37532/2320â6756.2021.9(1).204

Conformally Flat, Quasi-Circular Numerical Simulations of the Chirp from Binary Neutron-Star Merger GW170817

G. J. Mathews^*, I.-S. Suh, N. Q. Lan and A. Kedia

Center for Astrophysics, Department of Physics, University of Notre Dame Notre Dame, IN 46556, USA

*Correspondence:: G. J. Mathews
Center for Astrophysics, Department of Physics, University of Notre Dame Notre Dame, IN 46556, USA
E-Mail: gmathews@nd.edu

Received: December 31, 2020; Accepted: January 14, 2021; Published: January 27, 2021

Citation: Mathews GJ. Conformally Flat, Quasi-Circular Numerical Simulations of the Gravitational Wave Chirp from Binary Neutron- Star Merger GW170817. J Phys Astron. 2021;9(1):204.

Abstract

The first detection of gravitational waves a binary neutron star merger GW170817 by the LIGO-Virgo Collaboration has provided fundamental new insights into the astrophysical site for r-process nucleosynthesis and on the nature of dense neutron-star matter. The detected gravitational wave signal depends upon the tidal distortion of the neutron stars as they approach merger. We report on relativistic numerical simulations of the approach to binary merger in the conformally flat, quasi-circular orbit approximation. We show that this event serves as a calibration to the quasi-circular approximation and a confirmation of the valitiy of the conformally flat approximation to the three-metric. We then examine how the detected chirp depends the adopted equation of state. This establishes a new efficient means to constrain the nuclear equation of state in binary neutron star mergers.

Keywords

Gravitational waves; Nucleosynthesis; Polarizability

Introduction

On August 17, 2017, Nature revealed herself in a most spectacular way, both from the gravitational waves detected by the LIGO and VIRGO collaborations [1], and by the multitude of follow up observations [2], of the GRB170817A kilonova, along with IR and optical ground-based observations. In this work we consider two aspects of what may have been learned from this event. On the one hand, the GW chirp implies a possible dilemma regarding the Nuclear EOS deduced from the Post-Newtonian tidal-polarizability vs observed neutron star properties. Here we discuss our analysis of the chirp in numerical general relativity [3], as a means to better constrain the EoS and clarify the current dilemma. The second aspect considered here is that the kilonova EM spectrum indicates evidence of r-process nucleosynthesis that has implications for the fission barriers and termination of fission recycling during the r-process. In the LIGO analysis [1], and in follow up analysis [4,5] the tidal polarizability was deduced from post-Newtonian expansion. The tidal-polarizability (or deformability) is an intrinsic neutron-star property highly sensitive to the compactness parameter 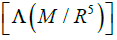that describes the tendency of a neutron star to develop a mass quadrupole as a response to the tidal field induced by its companion [6,7]. Based upon the most recent analysis by LIGO [5], it has been deduced that the reduced tidal polarizability is =190 + 390 -120 implying that the radius of the stars of 1.4 M is in the range 10.5 km ≤ R ≤ 13.3 km. However, in this work we consider the possibility that as the stars approach merger during the chirp they are neither well described by post-Newtonian physics, not as a simple quadrupole deformation. Indeed, one desires to trace the evolution of the binary from when they first enter the LIGO window until some 30 sec later when the stars merge. For an orbit period of 100 ms this would require evolving the system for 3000 orbits. This is indeed a daunting task from the standpoint of numerical relativity for which it is difficult to follow more than a few orbits due to limitations of computational resource. Here, we report on an analysis of a general relativistic hydrodynamic simulation [3-8], that is capable of stably numerically integrating thousands of orbits. The solution of the field equations and hydrodynamic equations of motion is summarized in [9,10], based upon the conformally flat condition on the spatial three-metric. In this approach, one begins with the slicing of space-time into the usual oneparameter family of hypersurfaces separated by differential dis-placements in a time-like coordinate as defined in the (3+1) ADM formalism [11,12]. In Cartesian x, y, z isotropic coordinates, proper distance is expressed as;

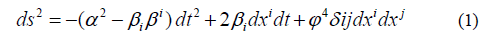
where the lapse function α describes the differential lapse of proper time between two hypersurfaces. The quantity βi is the shift vector denoting the shift in space-like coordinates between hypersurfaces. The curvature of the metric of the 3-geometry is then described by the conformally flat approximation, i.e. the spatial metric is described by a position dependent conformal factor Ø⁴ times a flat-space Kronecker delta 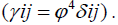This Conformally Flat Condition (CFC) on the metric provides a numerically valid initial solution to the Einstein equations. The vanishing of the Weyl tensor for a stationary system in three spatial dimensions guarantees that a conformally flat solution to the Einstein equations exists. However, the validity of this condition on the metric has never been established as a means to evolve the time-dependent evolution of a binary. One of the purposes of this paper is to confirm the validity of this approach. To solve for the fluid motion of the system in curved space-time it is convenient to use an Eulerian fluid description [9]. By introducing the usual set of Lorentz contracted state variables it is possible to write the relativistic hydrodynamic equations in a form which is reminiscent of their Newtonian counterparts [9]. The hydrodynamic state variables are: the coordinate baryon mass density D, the internal energy density E and the covariant spatial momentum density S_ii ;

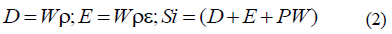
Key to maintaining stability is to evolve the spatial three velocities in the rotating frame;

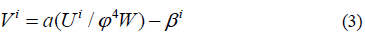
In terms of these state variables, the hydrodynamic equations in the CFA are as follows: The equation for the conservation of baryon number takes the form;

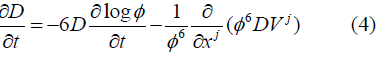
The equation for internal energy evolution becomes;

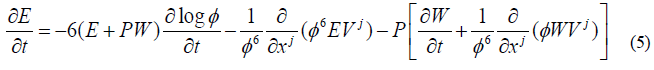
Momentum conservation takes the form;

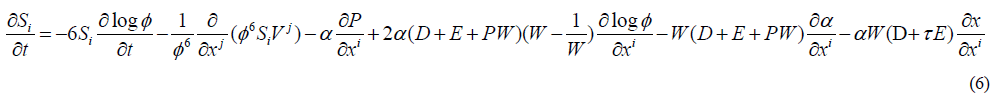
where the last term in Eq. (6) is the contribution from the radiation reaction potential χ as defined in Refs. [3-8]. Including this term allows for a calculation of the orbital evolution via gravitational wave emission in the CFA.

As a first test and calibration we have adopted the series quasi-stable orbits from [3-8] for which gravitational radiation loss is set to zero. The relative time of each orbit could be determined from the timescale for orbital energy loss by gravitational wave emission as described in [3-8],

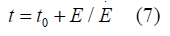
Where E is the orbital energy and the dot denoted a coordinate time derivative.

The entire chirp could then by constructed by fitting the numerical results for frequency vs. time with a modified power-law form of the chirp given by;

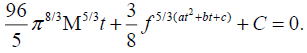
Here a, b and c are deduced from fits to the numerical simulation and correspond to corrections due to the inclusion of higher moments in density, gravity, mass-energy and momentum in the chirp. This correction is motivated by the observation that the deviation of a logarithmic f vs t plot from a straight line in numerical simulations is well represented by a simple quadratic curve.

A caveat of this approach, however, is that the time zero t0 for each series of orbits is not well defined. For our purposes we fixed the time zero at the point at which the slope of the chirp (df/dt) matches the slope of the LIGO observation. Since the slope is small, however, this introduces about a 10% uncertainty in the time-zero calibration. Nevertheless, as we show below, the differences among the various equations of state are so great, that this is an acceptable uncertainty.

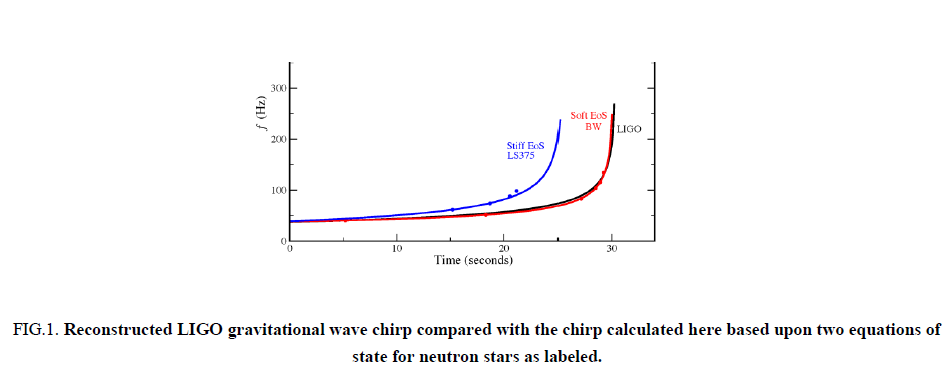
An example of the reconstructed chirp for two different equations of state are shown in figure 1 based upon orbits described in [3-8] of two nearly equal mass 1.4 M? neutron stars. The curve labeled BW is for the soft EoS of Bowers and Wilson [9], which leads to a compact neutron star. The cure labeled LS375 is based upon the extremely stiff, high incompressibility EoS from Lattimer and Swesty [13] for which a large neutron- star radius is implied. These extreme examples show a strong sensitivity to the nuclear EoS and are consistent with the sensitivity deduced from the PN analysis of tidal polarizability [1, 4].

Figure 1. Reconstructed LIGO gravitational wave chirp compared with the chirp calculated here based upon two equations of state for neutron stars as labeled.

This figure also establishes that the CFA in the quasi-circular orbit approximation can be used to reconstruct the chirp in a much more economical way than to attempt an exact fully relativistic simulation, while also including higher order corrections than the standard PN analysis.

Acknowledgment

This work was supported by the U.S. Department of Energy under grant DE- FG02-95-ER40934.

Review