Original Article
, Volume: 11( 6) DOI: 10.37532/2320-6756.2023.11(6).350Calculation of the space-time curvature in the vicinity of Schwarzschild black holes. Application to Sagittarius A*
- *Correspondence:
- Fernando Salmon Iza Bachelors in Physics from the Complutense University of Madrid UCM. Mathematics Teacher in a Secondary School, Spain, E-mail: fernandosalmoniza@gmail.com
Received date: 22-June-2023, Manuscript No. tspa-23-103521; Editor assigned: 22-June-2023, Pre-QC No. tspa-23-103521 (PQ); Reviewed: 26-June-2023, QC No. tspa-23-103521 (Q); Revised: 27-June-2023, Manuscript No. tspa-23-103521 (R); Published: 30-June-2023, DOI. 10.37532/2320-6756.2023.11(6).350
Citation: Iza F. S. Calculation of the Space-Time Curvature in the Vicinity of Schwarzschild Black Holes: Application to Sagittarius A*. J. Phys. Astron.2023;11(6):350.
Abstract
We have calculated values of space-time curvature in the vicinity of Schwarzschild black holes. For this we have used the metric and the results of Schwarzschild collected in his study on relativistic gravitation published in 1916 as well as techniques of differential geometry of surfaces. This has allowed us to obtain values of space-time curvature in the vicinity of Sagittarius A*, and thereby giving a physical content to our mathematical approach to the subject. The results are consistent with what was expected.
Keywords
Black holes; Curvature of space-time; Cosmology; General relativity
Introduction
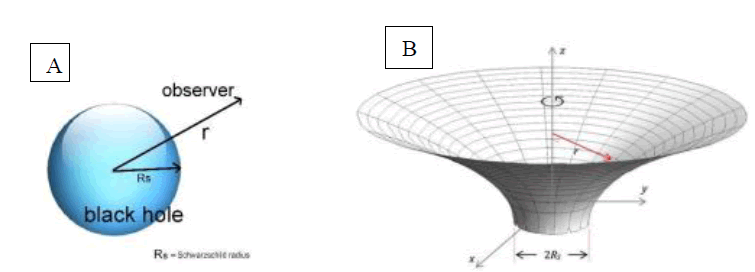
The physical problem that concerns us is the calculation of the curvature of space-time caused by a spherical black hole at a point located at a distance "r" from the center of the black hole. This point will always be at a greater distance from the event horizon or Schwarzschild radius, “Rs” also called this distance radius of the black hole. Schwarzschild solves the equations of the theory of generalized relativity for a supposition of a spherical mass and a surrounding empty space, establishing a metric and an equation of space-time that turns out to be the Flamm paraboloid [1]. This approach leads to a stationary space-time solution in time and the spherical symmetry of the problem geometrically simplifies its solution, resulting in a 2D surface, as represented in FIG. 1(A) and FIG. 1(B).
Figure 1: (A) The physical problem in Euclidean space (B) Space-time in the Schwarzschild metric Flamm paraboloid.
Resolution of the mathematical problem
Flamm's paraboloid, mathematical solution to the proposed physical problem, is a surface inserted in a space R3. Its geometry allows us to parameterize the paraboloid as a function of the observer's distance from the center of the black hole “r” and the azimuth angle "φ" .The problem admits a mathematical treatment of differential geometry of surfaces, and with it we are going to calculate values of Gaussian Curvature and Mean Curvature [2],
Surface parameters (r,φ)
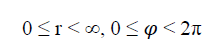
which has this parametric vector equation:
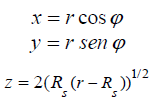
and by vector equation:
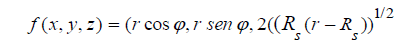
Determination of velocity, acceleration, and normal vectors to the surface,

Curvature and curvature parameters,
Gauss curvature:K=LN-M2/EG-F2
Mean curvature: H=GL-2FM+EN/2(EG-F2)
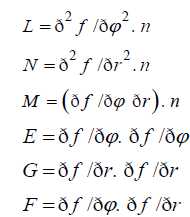
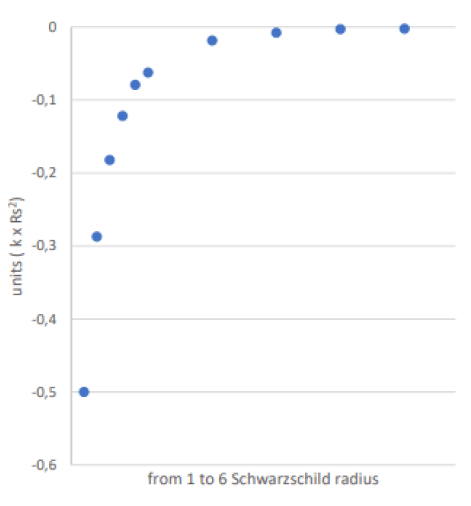
We have particularized the equations in 12 points between 1 and 600 Schwarzschild radii calculating the corresponding curvatures as shown in the results TABLE 1. Thus, although in the metric there is a singularity at the point 1Rs, in the value of the Gaussian curvature and mean curvature the singularity is resolved mathematically calculating a limit. We have calculated that limit for Gauss curvature and Mean curvature.
TABLE 1. Calculated curvature values.
| Distance to the center of the black hole | Value of Gauss Curvature (k) | Value of Mean Curvature (H) | |
|---|---|---|---|
| 1Rs | -0,5000 × Rs-2 | -0,2500 × Rs-1 | |
| C | 1,2Rs | -0,2873 × Rs-2 | -0,1888 × Rs-1 |
| U | 1,4Rs | -0,1821 × Rs-2 | -0,1509 × Rs-1 |
| R | 1,6Rs | 0,1220 × Rs-2 | -0,1236 × Rs-1 |
| V | 1,8 Rs | -0,0790 × Rs-2 | -0,1119 × Rs-1 |
| A | 2Rs | -0,0625 × Rs-2 | -0,0543 × Rs-1 |
| T | 3Rs | -0,0186 × Rs-2 | -0,0485 × Rs-1 |
| U | 4Rs | -0,0078 × Rs-2 | -0,0312 × Rs-1 |
| R | 5Rs | -0,0030 × Rs-2 | -0,0292 × Rs-1 |
| E | 6Rs | -0,0023 × Rs-2 | -0,0168 × Rs-1 |
| S | 60Rs | -2,3.10-6 × Rs-2 | -5,3.10-4 × Rs-1 |
| 600Rs | -2,8.10-9 × Rs-2 | -2,3.10-5 × Rs-1 |
Results of Curvature Values
According to the exposed mathematical approach, we have calculated curvature values at 12 points located at a distance between 1 and 600 Schwarzschild radii (Rs).
We have analyzed in more detail the width between 1 and 2 Schwarzschild radius, determining 5 points of curvature with at distance intervals of 0, 2 Schwarzschild radii. We have also calculated five points of curvature between 2 and 6 Schwarzschild radii, at distance intervals of one Schwarzschild radius. Lastly, we have calculated the curvature at two more distant points corresponding to 60 and 600 Schwarzschild radii.
Application to the calculation of the curvature in the vicinity of Sagittarius A*
Sagittarius A* is the supermassive black hole at the galactic center of the Milky Way. Like the nuclei of most spiral and elliptical galaxies, the Milky Way contains a black hole at its center. The mass of Sagittarius A* is estimated at 4 million suns, approximately 3.4×1036 Kg, its Schwarzschild radius, Rs, thus turns out to be 5×10 9 meters [3]. According to these data, the space-time curvature values in its vicinity turn out to be (TABLE 2):
TABLE 2. The space-time curvature values in its vicinity.
| Distance to the center of the black hole | Value of Gauss Curvature (k) | Value of Mean Curvature (H) |
|---|---|---|
| 1Rs | -2,0×10-20 m-2 | -0,5×10-10 m-1 |
| 1,2Rs | -1,1×10-20m-2 | -0,4×10-10 m-1 |
| 1,4Rs | -0,7×10-20m-2 | -0,3×10-10 m-1 |
| 1,6Rs | -0,5×10-20 m2 | -0,2×10-10 m-1 |
| 1,8 Rs | -0,3×10-20 m2 | -0,2×10-10 m-1 |
| 2Rs | -0,2×10-20m-2 | -0,1×10-10 m-1 |
| 3Rs | -0,7×10-21m-2 | -0,9×10-11 m-1 |
| 4Rs | -0,3×10-21m-2 | -0,6×10-11 m-1 |
| 5Rs | -0,1×10-21m-2 | -0,5×10-11 m-1 |
| 6Rs | -0,9×10-22m-2 | -0,3×10-11 m-1 |
| 60Rs | -9,2×10-26m-2 | -1,0×10-13 m-1 |
| 600Rs | -1,1×10-28m-2 | -4,6×10-15 m-1 |
Analysis of Results
We have obtained the results of the curvatures through a differential geometry approach, specifying the calculation in 12 points between 1 and 600 Schwarzschild radii. The calculation has been very laborious, and the results have been checked several times to verify their accuracy.
The curvature values are negative; this may imply a physical approach in the vicinity of the black hole to be considered in the future. The second is the finite value of the curvature at the event horizon or radius of the black hole, 1Rs. Although the Schwarzschild metric has a singularity in point 1Rs, there, this is mathematically avoided in the calculation of the curvature, resulting in a finite value of it. It should be noted that in the non-relativistic case, that is, for Newton's gravity, the curvature would be proportional to 1/r2, deviating noticeably from this assumption such as can be seen in FIG. 2 [4].
Using these results, we have calculated the curvature of space-time in the region close to a Schwarzschild black hole, this has allowed us to obtain curvature values in the vicinity of SAGITARIUS A*, and thus give a physical result to our mathematical calculations.
An equation for calculating curvatures in the vicinity of schwarzschild black holes
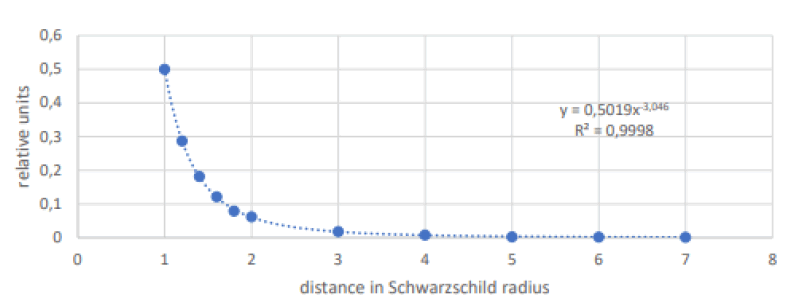
We are going to study the Gaussian curvature data by means of an equation obtained by fitting. Using an Excel program to determine the regression equation. We have not been able to obtain a function that fits all the data with a high degree of accuracy. For this reason, we have decided to fit only the data that are at distances from the center of the black hole between 1 and 7 Schwarzschild radii and for which we have found an equation that fits the processed data with a degree of accuracy of 99.98%. The result of the fit is the following (FIG. 3):
Figure 3: Comparison between the curvature values obtained by the Schwarzschild Model and those obtained by the fit equation.
Fit equation between 1 and 7 Schwarzschild radii:
Gaussian curvature: 
Fit quality: R2=0.9998
We express our formula as follows:
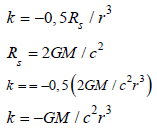
We are going to test our formula by calculating curvature values corresponding to the black hole Sagittarius A* and comparing them with those obtained by us in this study according to the Schwarzschild model.
As shown in the TABLE 3, the results obtained using the equation and the results obtained from the Schwarzschild model are similar, deviating slightly only in the value of the curvature at the point corresponding to a distance from the center of the black hole of 7 Schwarzschild radii.
TABLE 3. Results obtained using the equation and the results obtained from the Schwarzschild model.
| Mass of SAGITTARIUS A* =3,4×1036 Kg | G = 6,67×10-11 N.m2/kg2 | k = -GM/c2r3 | k = -2,52.109/r3 |
|---|---|---|---|
| Comparison between curvature values for SAGITTARIUS A* | |||
| Distance in Schwarzschild radius | Distance in meters | k = -2,52×109/r3 |
k (Values according to the Schwarzschild model) |
| 1 | 5.109 | -2,0.10-20 m-2 | -2,0.10-20 m-2 |
| 1.2 | 6.109 | -1,1.10-20 m-2 | -1,1.10-20 m-2 |
| 1,4 | 7.109 | -0,7.10-20 m-2 | -0,7.10-20 m-2 |
| 1,6 | 8.109 | -0,5.10-20 m-2 | -0,5.10-20 m2 |
| 1,8 | 9.109 | -0,3.10-20 m-2 | -0,3.10-20 m2 |
| 2 | 10.109 | -0,2.10-20 m-2 | -0,2.10-20 m-2 |
| 3 | 15.109 | -0,7.10-21 m-2 | -0,7.10-21 m-2 |
| 4 | 20.109 | -0,3.10-21 m-2 | -0,3.10-21 m-2 |
| 5 | 25.109 | -0,1.10-21 m-2 | -0,1.10-21 m-2 |
| 6 | 30.109 | -0,9.10-22 m-2 | -0,9.10-22 m-2 |
| 7 | 35.109 | -0,5,10-22 m-2 | 0,6.10-22 m-2 |
For this reason, we consider that the formula obtained is highly efficient in calculating curvatures of space-time in the vicinity of Schwarzschild black holes in the range of distances to the center of the black hole between 1 and 7 Schwarzschild radii.
Conclusion
Using the results of the Schwarzschild solution to Einstein's generalized relativity equations; we have calculated some values of space-time curvature in the vicinity of regular black holes. We have applied these results to the black hole of our galaxy SAGITTARIUS A*, calculating the curvature of space-time in its vicinity. Finally, we have obtained a formula that allows us to calculate curvature values at distances from the center of the black hole between 1 and 7 Schwarzschild radii obtaining excellent results with it when we have tested it for the case of SAGITTARIUS A*.
REFERENCES
- Schwarzschild K. On the gravitational field of a mass point according to Einstein's theory. arXiv preprint physics/9905030. 1999.
- Differential geometry of surfaces – Wikipedia [Google Scholar] [Crossref]
- Harwit M. Astrophysical concepts, Astronomy and astrophysics library (3.ª edition). Great Britain. Springer. ISBN 0-387-94943-7.1998:72-5. [Google Scholar] [Crossref]
- Iza F.S. A simple formula that allows to calculate the curvature of the trajectory in the Minkowsky space-time of a point located at a fixed distance from a point mass. J. Phys. Astron. 2023;11(4) [Google Scholar] [Crossref]