Original Article

, Volume: 5( 4)

• View PDF
• Download PDF

B. Feng’s Theory: The Prediction of Mass Spectrum of Elementary Particles and the Confidence of at Least 4-D Space-Time (PartⅠ)

*Correspondence:

Mei ZH College of Chemistry and Molecular Engineering, Qingdao University of Science and Technology, Qingdao, China, Tel: +86-0532-84022681; E-mail: mzh62@qust.edu.cn

Abstract

B. Feng’s series valuable works is introduced and improved in this paper. Based on Einstein’s four-dimensional space time in general relativity and the symmetry principle, B. Feng created his theory in field of elementary particle physics. He proposed 16-regular polytope to express the symmetries of elementary particles’ manifold in 4-D space. The manifold’s mode changing angle (δ) projected from 4D to 3D plays an important role in his theory. The mass spectrum of elementary particles is then predicted accordingly. The result formula is as:

Keywords

Elementary Particle; Four-dimensions; Mass spectrum; Symmetries; Superstring theory

Introduction

After the successful description of quantum mechanics, the focus at micro level of physics has removed from atom scale onto the subshell of elementary particles. Standard model and superstring theory become the landmarks in the field since 1964 and 1969. The prediction or explanation of mass spectrum of elementary particles (their regularly summarized work have done by several scientists in different ways [1-3] is one of the necessary tasks of the theories. Standard model is a well self-consistent theory. It showed us its clear view of the elements in subatomic scale. However, it exposed an embarrassed method in its theory, that it predicted the mass spectrum by pulling in as much as 19 experimental parameters even including quite some of the masses of elementary particles. The main fault is it can’t unify the four field forces and can’t tell the origin of charge etc, properties.

The superstring theory is considered to be an ideally the latest theory is that it eliminates all the defects of standard model with perfect symmetries mathematically. Its disadvantage is the difficulties in solving the exact solutions. Fortunately, a new proposed scheme [4-8] solved the problem wisely. It is called as B. Feng theory here and solemnly introduced and commented and improved in this paper.

General Introduction of B. Feng’s Theory

Personal information

Mr. Biao Feng was born in 1969 in China. As a teacher he worked in Zhanjiang Institute of Technology insisting on his lone favorite research work in field of fundamental physics for many years. He published several relevant papers in native language since 2010 and completed his theoretical system in about 2016.

Essential framework of the theory

The character of the movement of matter in subatomic scale is the satisfaction of symmetries in its physical dimension space. In present theory, Einstein’s 4-D space time concept was adopted and the symmetries exhibit among the 4-D physical space. The elementary particles and their properties to us (3D) are the projections of 4-D movements of subatomic matter. In other words, as the symmetries decrease with dimensions, the physical quantity is created by projection. The structures and properties of elementary particle are essentially that of the topology of manifold. B. Feng didn’t mentioned any words referred or related to the famous theory of superstring in his theory, nevertheless his mathematical world view of physics is somehow like that of the superstring. The highlight point is that, unlike superstring theory (one-dimensional strings vibrating in several patterns in curved 11-D space), the B. Feng’s does not describe the detailed patterns of motion mathematically; therefore one has no trouble for solving those unsolvable equations. In B. Feng’s theory, the resolutions are actually present by the natural matter world. We just need to collect and distinguish and unity them by symmetry method, no bother to do the fussy ab initial calculations.

In B. Feng’s theory, the introduced parameters are integer natural numbers, geometric numbers and general universal constants and laws. Only two arbitrary parameters are introduced in. One is about the photon which was assumed to be the essential measuring reference; the other is referred to curved space.

Achievements of the theory

In B. Feng’s theory, one can predict the kinds of elementary particles and calculate the mass spectrum. Other essential such as charge and spin etc. attribute can all be predicted in the powerful theory. Furthermore, it can derive or calculate some physical constants such as Planck’s constant and Hubble constant. The key point is that, it can unify the Four Field Forces to some extent.

As the B. Feng’s theory contains so many items, just the mass spectrum calculating part is introduced and improved in this paper for an easy reading.

Experimental

Primary part of B. Feng’s theory

The supersymmetry of four-dimensional spherical surface can be expressed by 4-D regular polytope. There are six kinds of regular polytopes in 4-D in geometry. The cells are 5, 8, 16, 24, 120 and 600 respectively.

Assumption 1: As the fourth dimension of time (T) is exist in imaginary form (ict) with the speed of light in four-dimensional space, the world is then half measurable and the other half is immeasurable. Photon is assumed to be the essential manifolds of space-time (?0 is expressed its curvature). The quantum photonic base is the particle at critical point; it contains two sides of measurable and immeasurable ones. All other elementary particles manifolds’ curvature (ρ) is quantized to be n times of photon’s, as 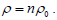Expressed in radius of curvature (R), we have,

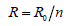(1)

Where, n is positive integer.

As the ratio of volume (V) equals the inverse ratio of cells number to regular polytopes, so in four dimension space we have,

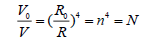(2)

Where, n is positive integer and N the cells number.

Solving the equation in (2), the apparent solution is only that of n = 2 , and N = 16 . It showed us that the elementary particles’ manifolds of space time can only express by 16 cells of regular polytopes and its radius of curvature is then appeared to be multiple relationship of 2.

Reasoning

According to above assumption, the elementary particles are consisted of photonic base. It is equality to say reversely that the photonic base is consisted of elementary particles in size.

Every side of photonic base has radius of curvature of R₀, then total photonic base has the radius of curvature of 2R₀. The elementary particle is measurable and a single cell’s radius of curvature is R; as to 16-regular polytopes, the total radius of curvature is then 16R. In geometrics, the important relation is that the total radius of curvature of 16-regular polytopes is bigger than that of total photonic base, expressed as 0 16R > 2R₀ , or rearranged as:

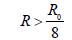(3)

As mentioned above that, R has multiple relations of 2. Then the R has three probable values, expressed as:

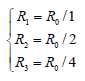
Or

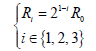(4)

Where, i is the layer number. Three values of R_i correspond to three layers of structure of matter. And photonic base quantum is a single cell of 1 kind particle.

In layer 1, it contains 16 cells of photonic base, as half of them are measurable, the kinds of particles are 16/2=8.

In layer 2, it contains 16 cells of layer 1, as half of them are measurable, the kinds of particles are 8 × 8=64.

In layer 3, it contains 16 cells of layer 2, as half of them are measurable, the kinds of particles are 8 × 8 × 8=512. However, almost all of them are extremely unstable.

So, the total kinds of elementary particles can calculate as (not concluding the anti-particles):

(1+ 8 + 64) = 73 (5)

The projections’ quantitative expression of 16-regular polytopes in 3-D is mode changing angle (expressed by δ). The mode changing angle contains two parts, the shape mode changing angle (δ_R) and position mode changing angle (δ_W) and can expressed by:

δ=δ_R+δ_W

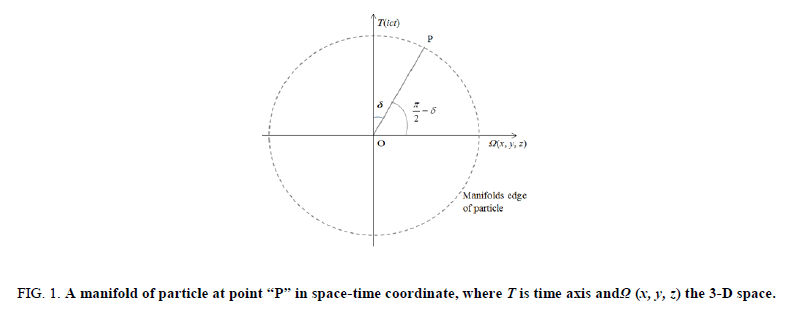
As to photonic base, δ_R0=3/π, δ_W0=π/2 (photonic base along the vertical time axis, shown in Figure. 1)

As to layer 1 particles, δ_R1=2π_R0/_R1=2π, δ_W1=δ_W0+(4π/16) J₁=π/2+(4π/16) J₁

As to layer 2 particles, δ_R2=2π_R0/_R2=4π, δ_W2=δ_W1+(4π/16/16) J₂=π/2+(4π/16) J₁+(4π/16/16) J₂

As to layer 3 particles, δ_R3=2π_R0/_R3=8π, δ_W3=δ_W2+(4π/16/16/16) J₃=π/2+(4π/16) J₁+(4π/16/16) J₂+(4π/16/16/16) J₃

Where, J is sequence number of position and 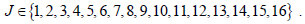. As half of them is immeasurable, then for measurable particles,

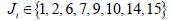(6)

For convenient, we may call J₁ to be the quantum number of the “1” layer and J₂ of the “2” layer, J₃ of the “3” layer. And a particle’s state can express by symbol, B (J₁, J₂, J₃). For a particle in “1” layer, it contains one quantum number and can express by B (J₁); for a particle in “2” layer, it contains two quantum number and express by B (J₁, J₂).

Calculating of Mass Spectrum of B. Feng’s Theory

Derivation of mass calculating formula

According to the equivalence of mass (m) and energy (E), we have 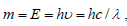, using the perimeter of manifolds instead of λ , we have,

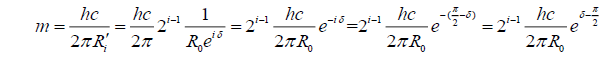
Where, R_i’ is the projection of R_i and e^iδ is the projection factor compared with photonic base, as the photonic base is at the direction of time axis; δ is the angle of a particle to imaginary time axis and 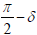is then to real space axis. It shows clearly in Figure. 1.

As to photonic base, we choice the critical value of wave-particle duality energy (E₀) of 2.5985 eV (468.69 nm, a blue color), one can continued as:

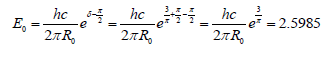
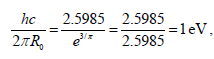so for a particle we obtained the formula as:

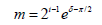(7)

Illustrating of application

In order to exhibit the charming formula (7) clearly, the details of some of the calculation processes is expanded respectively, rather than simply list the results in table.

As to electron, the structure symbol is B(9), then,

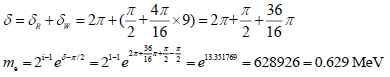
(Real measured value is 0.511 MeV)

As to proton, symbolled by B (9, 7), thus:

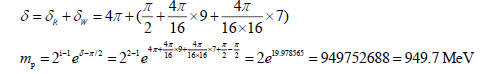
(Real measured value is 938.3 MeV)

As to electron neutrino, symbolled by B (1), then,

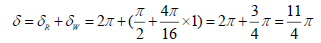
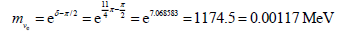
(Real measured value less than 0.00002 MeV)

As to μ neutrino, symbolled by B (7), then,

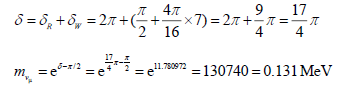
(Real measured value less than 0.16 MeV)

As to τ neutrino, symbolled by B (14), then,

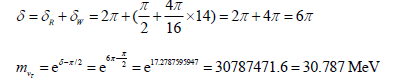
(Real measured value less than 31 MeV)

Effect of curved space (Improved part of B. Feng’s theory)

According to Einstein’s general relativity, the mass will cause an apparent curvature in its nearest space and so is in micro elementary particles. In subatomic scale, the space is no longer a Euclidean one, but Riemann’s; the 16-regular polytopes is then curved. As a consequence, the direction mode changing angle at the outmost layer must be adjusted by a factor (k), however the shape mode changing angle is remained.

Assumption 2: Considering the effect of curved space, the direction mode changing angle of outmost layer is arbitrarily adjusted by a factor k, and

k = 0.970624 (8)

From this, the adjusted mode changing angle δ’ can express as:

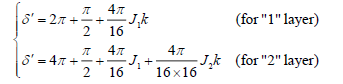(9)

Using δ’ instead of δ in formula (7), one can recalculate some masses as following,

Results and Discussion

Proton has the structure symbol of B (9, 7). Then the next particle would symbolled by B (9, 8) and it has overlarge mass value than that of proton. It is a kind of particle but not the neutron. It showed us that neutron is not an elementary particle but a composite one in the B. Feng’s theory.

Proton is then an elementary particle here; it can’t be consisted of other elementary particles such as quarks that proposed in Standard Model.

The predict electron neutrino’s mass would has large deviations compared with experimental because of its less value at magnitude of about keV level. It is comprehensible, that when the energy is below about keV, the symmetry would break severely [9].

Einstein’s four-dimensional space time is the basis of B. Feng’s theory. The success of B. Feng’s theory indicates that real physical space is at least four-dimensional space time in subatomic scale. As we know, the effect of Einstein’s four-dimensional space time only appears when velocity is nearing the light, however the particles we are treated are all at rest. How can we treat with it? The only reason is that the demand of 4-D space time of the theory means that the mass origin (or the formation mechanism) is the confined movement of light [10]; so it must be in Einstein’s 4-D space-time.

Conclusion

The frame work of B. Feng’s theory is perfect. Their result in the calculation of mass spectrum is satisfied. However, some aspects of it are immature at present and needed further developing. The success of B. Feng’s theory convinced physicists the existence of at least 4-D space time in subatomic scale.

References

1. Balogh V, Seelig W, Straub D. Zur Berechnung der Elementarteilchen-Masse. University of the Federal Armed Forces Munich. 1997.
2. Dieter Straub. Vilmos Balogh. Rest masses of elementary particles as basic information of Gibbs-Falkian thermodynamics. Int J Therm Sci. 2000; 39:931-948.
3. El Naschie MS. On the exact mass spectrum of quarks. Chaos Solitons and Fractals. 2002; 14:369-376.
4. Feng B. A structure analysis of the fundamental particles. Journal of Wuyi University. 2016; 30:15-23.
5. Feng B. A mathematical-physic analysis of unmeasured sets. Journal of Wuyi University. 2016; 30:21-27.
6. Feng B. The topological analysis of material structure. Journal of Wuyi University. 2013; 27:42-49.
7. Feng B. An analysis of modal changes in cosmic space. Journal of Wuyi University. 2012; 26:29-36.
8. Feng B. The measurement analysis of the physical space. Journal of Wuyi University. 2010; 24:33-38.
9. Mei ZH. The golden ratio breaks. Discovery. 2017; 53:498-504.
10. Mei ZH, Mei SY. Mass the confined movement of energy. Journal of Modern Physics. 2017; 8:923-925.