Review
, Volume: 6( 1)B. Feng’s Theory (Part Ⅲ): Neutron Model and Nuclei Force Mechanism.
- *Correspondence:
- Mei ZH, College of Chemistry and Molecular Engineering, Qingdao University of Science and Technology, Qingdao, China, Tel: +86-0532-84022681; E-mail: mzh62@qust.edu.cn
Received: March 12, 2018; Accepted: March 21, 2018; Published: March 28, 2018
Citation: Mei ZH. B. Feng’s Theory (Part Ⅲ): Neutron Model and Nuclei Force Mechanism. J Phys Astron. 2018; 6(1):143
Abstract
According to B. Feng’s theory, a new neutron model and nuclei model are proposed. The strong interaction as the original electromagnetic is proved by calculation; also the weak interaction has been deeply discussed.
Keywords
Electron radius; Neutron; Nuclear model; Unified field theory
Introduction
We have proposed a series of papers as partⅠ[1] and partⅡ[2] for exhibit our subject of B. Feng’s theory, and this time we propose the part Ⅲ in order to complete the frame work of Unified Field Theory, i.e., we will state how we can unified the nuclei force as the consequence of the electric charge in this paper.
As the neutron has been concluded to be a composite particle, then an evident question is that what the structure it has? Its answer is the first job of the paper and the key point of nuclei forces.
Neutron and Nuclei Model
Electron needs his size in radius
An important thing is that if we knew the radius of electron in the field of elementary matter particles! Though the electron has its characters in wave on the one hand, as a fundamental particle, electron was demanded to has its approximately classical radius is however reasonable and meaningful. Usually the electron was used as the tool to measure the size of other heavy particles in microscale. But how can we do for measuring itself. Maybe the size of electron cannot be directly measured indeed. It seems the only way is that the radius of electron could be reasonably assumed or cognized theoretically. Its correctness can wait for later validation or modification by its applications.
According to Rutherford’s dispersion experiment of α particles on gold target, the radius of a nucleon was calculated to be 1.2598 × 10−15 m, where the nucleus including the neutron and proton in gold atomic nuclear were treated as contact tightly with one another and possessing the same size in radius (Erdei, 1976). However, may that’s not the real case according to our theory. As the neutron is a composite particle and one will see in next paragraph, the radius of proton is much small than electron, so it seems that the electron has the same radius with neutron [3] with nearly twice value of 1.2598 × 10−15 m, thus we suggest the more reasonable electron radius of 2.51620 × 10−15 m instead of which we guessed in former literature [4].
Question Proton Radius
Proton’s radius is known as 1.2598 × 10−15 m. However, according to our theory in literature [2] equation (1) we have,
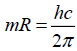 , so as to proton (subscript by letter “p”) and electron (subscript by letter “e”) we have,
, so as to proton (subscript by letter “p”) and electron (subscript by letter “e”) we have,
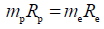
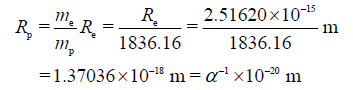 (1)
(1)
To our surprise, the radius of proton is much smaller than electron. It challenged our traditional physical views thoroughly.
Modeling Neutron
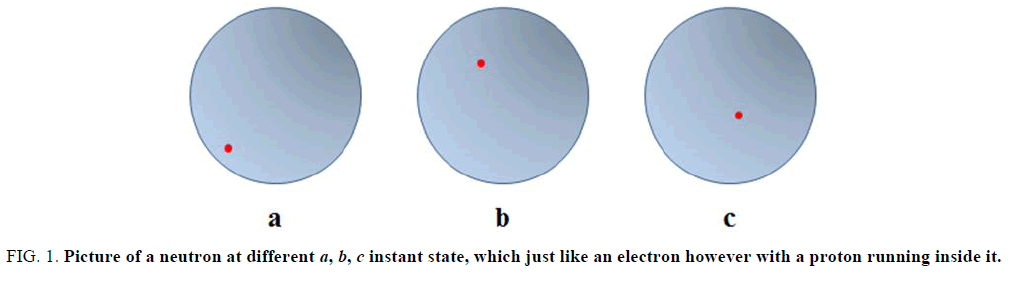
Since neutron is consists of proton and electron, and proton is much small than electron in size, we can imagine the neutron’s structure is just that a proton running inside an electron, as shown in Figure 1.
Figure 1: Picture of a neutron at different a, b, c instant state, which just like an electron however with a proton running inside it.
In this way, how is the composite neutron become to be? It is in fact that, a proton was compressed into an electron. The detail is as follows:
As we known, atom is successfully described by quantum mechanics. The electrons can run around nucleus at different quantum states including exited ones. In quantum theory, an electron orbit can be stable spontaneously in ground state in atom, but it is forbidden if its orbital radius is smaller than Bohr’s (5.29 × 10−11 m). Now it seems that, the quantum description is not a perfect, because in another side the electron could be forced to run with orbital radius smaller than Bohr’s when it (the atom system) was compressed by surroundings, an additional energy must exerted to. It is because of that it bent the original mass formation motion of electron. The additional energy and the inner charge potential energy becomes the additional mass of the system and energy release. With the orbital radius decrease, the repulsive “distortion force” will increase at first and then decrease, and further it will download to zero when proton has been compressed completely into electron; the familiar particle of neutron is then formed. A deep theory is needed later for describing the processes quantitatively. It must be emphasized that the attractive force between charged proton and electron is remained; however the repulsive distortion force is dominant in the process of neutron formation.
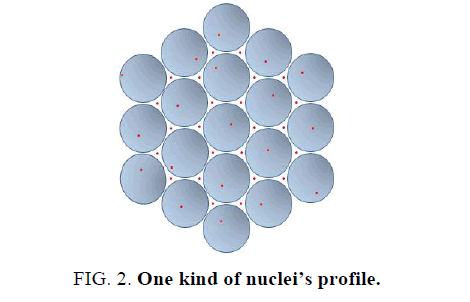
Modeling Nuclei
As the proton is so small than neutron, one can imagine the nuclei structure is just like that the closer packed neutron balls with protons inside their interspace. The neutron balls are packed like metal crystal accumulation modes however are mostly based on tetrahedral element. Every tetrahedral void must have a proton. As to the surface of closer packed balls, every “three balls gap” may permit with a proton or without. So to a certain number and types of neutrons’ nuclei, their possessing protons have an exact minimum and maximum number, and can calculate or easily account by structure model. It means that for an unsaturated nucleus, a new added proton must be on the surface of the nucleus and combine with 3 neutrons in the three ball gap. A sectional view of a regular nucleus is showed in Figure 2.
Nuclei Force Mechanism
The strong interaction
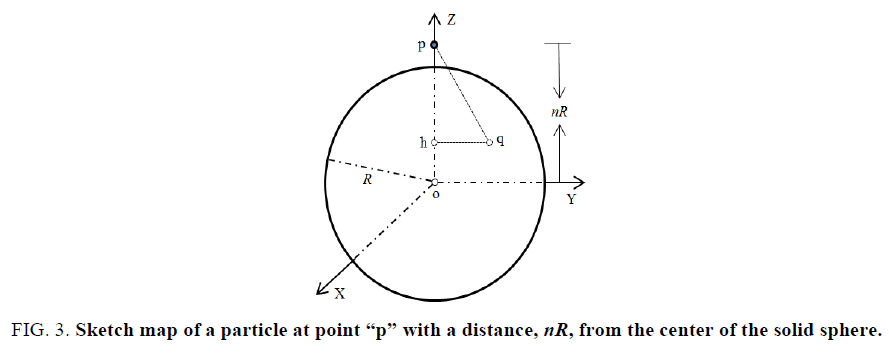
According to above models, we can calculate the nuclei force by means of charge interactions. As to a neighboring large body, the radius of the body cannot be neglected, or to say that the electron cannot be treated as point charge; its accurate result can be obtained by processing a mathematical integral.
Taking the electron as a volume charged particle (inflexibility) here, the calculating method of the interaction force between
charges can reference literature [4] of formula (1). As Figure 3 expressed, a solid spherical electron has a radius of R, a
homogeneous charge density of ρ; point “q” is the arbitrary point in the solid sphere, “h” the point corresponding to “q”
horizontally, 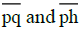 stand for the corresponding points distance,
stand for the corresponding points distance, 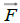 the vector force, dq the point charge, F1 the force
between proton and “electron”, F2 the force between proton and the proton inside neutron; the proton at point “p” has a
distance, nR, from the center of the solid sphere, the between attractive force, F(n), was derived as follows:
the vector force, dq the point charge, F1 the force
between proton and “electron”, F2 the force between proton and the proton inside neutron; the proton at point “p” has a
distance, nR, from the center of the solid sphere, the between attractive force, F(n), was derived as follows:
Figure 3: Sketch map of a particle at point “p” with a distance, nR, from the center of the solid sphere.
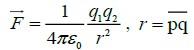
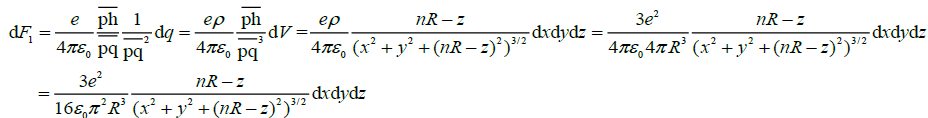 (2)
(2)
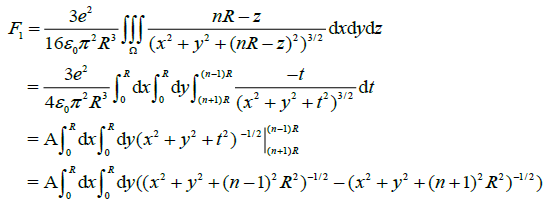
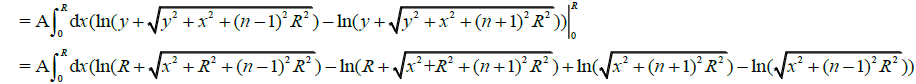 (3)
(3)
 (4)
(4)
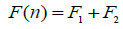
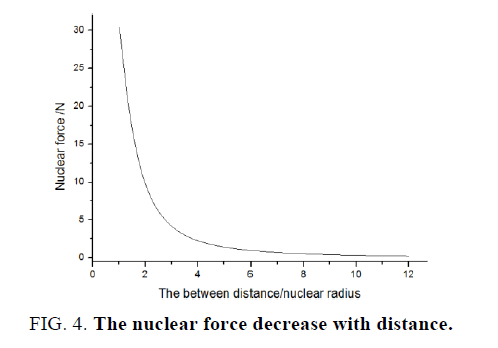
Solving the function graphically, one can obtain a series of data F(n) which corresponding to different n. Their relationship is showed in Table 1 and Figure 4.
| n | 1 | 1.01 | 1.02 | 1.04 | 1.06 | 1.08 | 1.10 | 1.12 | 1.14 | 1.16 | 1.18 | 1.20 | 1.22 | 1.24 | 1.26 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F(n) | 30.68 | 30.37 | 30.19 | 29.63 | 29.00 | 28.35 | 27.69 | 27.04 | 26.40 | 25.77 | 25.15 | 24.54 | 23.95 | 23.37 | 22.81 |
| n | 1.28 | 1.30 | 1.32 | 1.34 | 1.36 | 1.40 | 1.42 | 1.46 | 1.48 | 1.52 | 1.54 | 1.58 | 1.62 | 1.64 | 1.68 |
| F(n) | 22.25 | 21.72 | 21.19 | 20.68 | 20.19 | 19.23 | 18.78 | 17.90 | 17.48 | 16.67 | 16.28 | 15.53 | 14.83 | 14.50 | 13.85 |
| n | 1.70 | 1.74 | 1.80 | 1.84 | 1.88 | 1.92 | 1.96 | 2.00 | 2.10 | 2.15 | 2.20 | 2.25 | 2.30 | 2.40 | 2.50 |
| F(n) | 13.54 | 12.95 | 12.12 | 11.60 | 11.12 | 10.66 | 10.22 | 9.81 | 8.87 | 8.45 | 8.05 | 7.68 | 7.33 | 6.70 | 6.14 |
| n | 2.60 | 2.70 | 2.80 | 2.90 | 3.00 | 3.10 | 3.15 | 3.30 | 3.40 | 3.60 | 3.80 | 4.00 | 4.20 | 4.40 | 4.60 |
| F(n) | 5.65 | 5.21 | 4.82 | 4.47 | 4.15 | 3.87 | 3.74 | 3.38 | 3.18 | 2.81 | 2.50 | 2.24 | 2.02 | 1.83 | 1.67 |
| n | 4.80 | 5.00 | 5.50 | 6.00 | 6.50 | 7.00 | 7.50 | 8.00 | 8.50 | 9.00 | 10.0 | 10.5 | 11.0 | 11.5 | 12.0 |
| F(n) | 1.53 | 1.40 | 1.15 | 0.96 | 0.81 | 0.70 | 0.60 | 0.53 | 0.47 | 0.42 | 0.33 | 0.30 | 0.28 | 0.25 | 0.23 |
Table 1: Data of the nuclear force F(n) corresponding with distance nR.
The integral of F(n) over n is calculated graphically and resulted as,
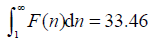
For a single neutron with proton, the combined energy is,
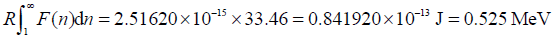
As mentioned above, the additional proton will combine with three neutrons, so the total binding energy (E) would be,
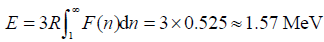
Results and Discussion
The weak interaction
According to our nuclei model, it is clear that, except proton-neutron interaction, the between neutrons or protons must interact each other. As they are separated by their radius or the distance of the tetrahedral voids, their interaction strength will be smaller than the strong interaction off about a half. That’s why we called it the weak interaction, and the weak interaction is a complex. The between neutrons interaction is resulted a repulsive force, because it is as a whole looks like the electrons with closely contacted. It is easy proved to be a short-range force by calculation; furthermore, the range would be shorter than the strong force due to its double none charged.
The most important is the interaction between protons. It is purely electromagnetic mechanism and has a long-range acting. The protons can vibrate (or move) in their tetrahedral voids. The vibrations of the protons are related and synergetic like a mode however three-dimensional. It has its eigenvalues in frequency of vibration. Large nuclei would have more and lower eigenvalues, and the more and lower eigenvalues means more capacities for absorbing energy from surroundings and also means high probability for accumulating high vibration energy. And one certain high vibration energy would influence the motion of “proton” which inside neutron and processing energy transfer and forced the inside proton exit out of neutron, with spontaneously ejecting, and energy releasing (a reverse process of neutron formation), the nuclear decay process then takes place. This is the reason for explaining the stabilities of heavy atoms. According to our model, we insist on the present theory as “quantum electrodynamics” or its improved version for dealing with the weak interaction quantitatively. The quantum electrodynamics theory for the weak interaction is the golden key for manipulating the nuclei and will has a great application value.
Obviously, our calculated nuclear binding energy resulted as 1.57 MeV. It is at the same order of magnitude with the actual measured value of 2.23 MeV. The quite missing part may because of the unconsidered deformation effect of neutron, like the ion polarization in chemistry; maybe other reasons must be also included, e.g. nuclear magnetic. If one would like to obtain an accurate value, the nearby nucleons must be concerned complicatedly.
We treated the “electron” as a volume charged particle is suitable; if it was treated as a surface charged, the nuclear binding energy would result as only 3 × 0.167=0.50 MeV. And also, chosen electron and neutron radius as 2.51620 × 10−15 m is reasonable; otherwise, if it was to be as 1.2598 × 10−15 m, the resulted nuclear binding energy would be an unacceptable negative value of −3.29 MeV, and this becomes important evidence for electron radius.
Figure 4 showed that the nuclear force decreased sharply with distance. As the nucleons are apart at distance of about ten times the radius of neutron, i.e., 10−14 m, the strong force will disappear thoroughly. If the separation distance is as long as 7.88234 × 10−8 m, the nuclear force was calculated to be exactly zero or negative value. That is just as known the short-range force. This typical characteristic comes from the typical neutron model and the typical small size of proton.
The above mentioned “distortion force” looks like a new types of force, however it is constitutionally the same electric charge interaction. Because the distortion changed the forms of charge formation motion; it is to say that the distortion enhanced the particle’s electric charge value. In other words, the value of fundamental electric charge of elementary particles is a changeable by its distortion.
From equation (1), we obtained an unexpected harvest that the proton radius is right the inverse fine structure constant, α−1. It may means something in physics.
Another thing we discovered that the charge effects of the inseparable elementary particle electron can be treated as differential and integral in space.
By the way, as proton’s need, we have arrived at the smallest physical scale in space in order of magnitude of 10-18 m.
Conclusion
The proposed neutron and nuclei model result the satisfied explanations of the strong interaction and the weak interaction in nuclei. These two interactions are all also original electromagnetic. Thus, the problem of unified field theory has been completely solved. Those, alongside the weak charge, strong charge and gluon etc. concepts in standard model are all unacceptable and absurd in fundamental physics.
References
- Mei ZH. B. Feng’s Theory: The prediction of mass spectrum of elementary particles and the confidence of at least 4-D space-time (PartⅠ). Journal of Physics & Astronomy. 2017;5:126-132.
- Mei ZH. B. Feng’s Theory (Part Ⅱ): The origin of charge and the Unified Field Theory-Going on Kaluza-Klein’s. Journal of Physics & Astronomy. 2018;6(1): 131-139.
- Zhen-hua Mei, Shu-yu Mei. No needs of neutrinos in theoretical calculation of βdecay. Indian Journal of Science. 2013;3(6): 11-14.
- Zhen-hua Mei, Shu-yu Mei. A guess of reasonable electron radius and overlapped model of nuclear force. Indian Journal of Science. 2013;3(8):85-87.