Short communication
, Volume: 13( 2) DOI: 10.37532/2320-6756.2025.13(2).403About the Experimental Study of Nonlocality in Quantum Physics
VA Kuzmenko*
Department of Physics, Troitsk Institute for Innovation and Fusion Research, Moscow, Troitsk, Russian Federation
- *Correspondence:
- VA Kuzmenko
Department of Physics, Troitsk Institute for Innovation and Fusion Research, Moscow, Troitsk, Russian Federation
E-mail: kuzmenko@triniti.ru
Received: April 02, 2024, Manuscript No. TSPA-24-131221; Editor assigned: April 05, 2024, PreQC No. TSPA-24-131221 (PQ); Reviewed: April 19, 2024, QC No. TSPA-24-131221; Revised: March 07, 2025, Manuscript No. TSPA-24-131221 (R); Published: March 14, 2025, DOI. 10.37532/2320-6756.2025.13(2).403.
Citation: Kuzmenko VA. About the Experimental Study of Nonlocality in Quantum Physics. J Phys Astron. 2025; 13(2). 403.
Abstract
There is a long-forgotten experiment in quantum physics in which nonlocality manifests itself in a quite direct and obvious way. The basic properties of nonlocality can be experimentally studied there using very simple tools.
Keywords
Entanglement; Time reversal noninvariance; Quantum memory; HOM effect; Nonlocality
Introduction
The concept of nonlocality is strongly connected with quantum physics. It is also associated with the concept of entanglement. “Entanglement, according to Erwin Schrodinger the essence of quantum mechanics, is at the heart of the Einstein-Podolsky-Rosen paradox and of the so called quantum-nonlocality-the fact that a local realistic explanation of quantum mechanics is not possible as quantitatively expressed by violation of Bell’s inequalities” [1]. The discussion and study of the problem of nonlocality in quantum physics began with the famous work of Einstein-Podolsky-Rosen on the incompleteness of quantum mechanics and the possible “spooky action at a distance” [2].
Description
The problem of nonlocality in quantum physics has long been actively discussed in the scientific community [3]. To date, the experimental study of nonlocality usually consists of creating a rather complex optical scheme with entangled photons, carrying out measurements and calculations. The so-called Bell or Clauser-Horne-Shimony-Holt (CHSH) inequalities are calculated [4]. Violation of these inequalities indicates a certain nonlocality. However, it is not clear what the physical essence of this nonlocality is.
The situation is similar in general with quantum mechanics. This is a mathematical theory based on the Schrödinger equation. It is claimed, that it brilliantly describes the experimental results. However, it does not have any clear physical meaning. For many decades, attempts have been made to give it a physical interpretation. “New interpretations appear every year. None ever disappear” [5]. Obviously, the situation is at deadlock. Philosophers say that in this case a paradigm shift is needed. Such a paradigm in quantum mechanics is the idea of time symmetry. The prevailing point of view is still that”. a remarkable fundamental fact of nature: all known laws of physics are invariant under time reversal” [6].
At the same time, for many years there have been a number of direct and a huge number of indirect experimental proofs of the nonequivalence of forward and reversed processes in quantum physics [7]. It is difficult to understand why our scientific community stubbornly ignores this experimentally proven fact. The recognition of the non-invariance of time reversal in quantum physics makes it easy and natural to explain the physical nature of entanglement and nonlocality.
If the forward and reverse processes are not equivalent, then there must inevitably be some kind of memory of the quantum system about its initial state. Without such memory, it is impossible to distinguish a direct process from a reversed one. This memory (as the physical equivalent of entropy) is the physical essence of the concept of entanglement. Entanglement is a memory of quantum system about its initial state, which manifests itself through inequality of differential cross-sections of forward and reversed processes [8]. The difference in differential cross-sections can be many orders of magnitude. In fact, this is the physical basis for most effects in nonlinear optics.
Nonlocality, obviously, is a property of this memory. We don't know where this memory is stored, but we can experimentally study its nonlocal properties. The experiment has been known for many years in which the nonlocal memory of a quantum system manifests itself in a completely direct and obvious way. We are talking about the experiment performed in [9]. The authors of this work did not understand what kind of thing they are dealing with and this experiment (direction) is practically forgotten today. Below we will discuss the details of this experiment and indicate the directions of its development.
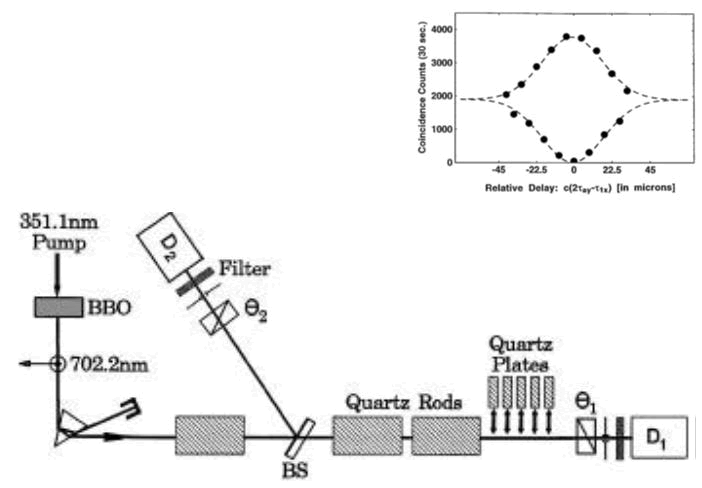
Figure 1 shows the scheme of this experiment and its result [9]. Here, the Hong-Ou-Mandel (HOM) effect was studied using collinear entangled photons obtained by down conversion in a nonlinear type II crystal. The delay between photons was regulated by quartz plates, in which photons with different polarizations propagate at different speeds. Two entangled photons arrive at the beam splitter and then enter at two detectors D1 and D2. When photons were synchronized with quartz plates, a typical HOM effect was observed.
The most interesting thing here is that the manipulations with quartz plates are carried out after the beam splitter, but not before it (as in the vast majority of works). It looks like a violation of causality. The splitting of photons by a beam splitter (consequence) precedes the cause (plates manipulation). However, it is not about the violation of causality, of course. We are dealing with an obvious manifestation of nonlocality. The photons, coming to the beam splitter, in some mysterious way “know” what will happen later and behave accordingly.
FIG. 1. Scheme of the experiment and its result.
This situation is completely analogous to that which exists in the classical two-slit interference. When a photon or electron passes through a slit, it somehow mysteriously "knows" about the existence of the second slit [9,10]. In the case of slits, for various reasons, we cannot spread them far apart. However, in the case of the HOM effect, we can separate the beam splitter and quartz plates at least several kilometers away [11]. We can experimentally study in this way nonlocality of quantum memory. 10 m, 100 m, 1000 m, 10 km. At some distance the HOM effect should disappear. In this case, we will get an idea of the degree of nonlocality of the memory of this quantum system.
Then we can try to determine how fast this “knowledge” spreads. If a high-speed Pockels cell is used instead of quartz plates to synchronize photons (as in [12]), then in the version of the so-called “delayed choice” [13-16], the speed of information (memory) propagation in space can be measured. Could this speed be greater than the speed of light?
Conclusion
The experiments discussed today are very simple. There are a large number of experimenters who have all the necessary equipment for such experiments. We hope that someone will at last carry out these important, interesting and simple experiments.
References
- Brukner C, Zukowski M, Zeilinger A. The essence of entanglement. In: Jaeger, G., Simon, D., Sergienko, A.V., Greenberger, D., Zeilinger, A. (eds) Quantum Arrangements. Fundamental Theories of Physics, vol 203. Springer, Cham. 2001.
- Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete?. Phys Rev. 1935;47(10):777.
- Genovese M, Gramegna M. Quantum correlations and quantum non-locality: A review and a few new ideas. Appl Sci. 2019;9(24):5406.
- Brunner N, Cavalcanti D, Pironio S, Scarani V, Wehner S. Publisher’s note: Bell nonlocality [rev. mod. phys. 86, 419 (2014)]. Rev Mod Phys. 2014;86(2):839-840.
- Mermin ND. Commentary: Quantum mechanics: Fixing the shifty split. Phys Today. 2012;65(7):8-10.
- Davies PC. The physics of time asymmetry. Univ of California Press; 1977.
- Kuz’menko VA. Time reversal noninvariance in quantum physics. e-print, viXra. 2004;10.
- Kuz’menko VA. On the physical nature of entanglement. e-print, viXra.;2305.
- Pittman TB, Strekalov DV, Migdall A, Rubin MH, Sergienko AV, Shih YH. Can two-photon interference be considered the interference of two photons? Phys Rev Lett. 1996;77(10):1917.
- Greenstein G, Zajonc A. The quantum challenge: Modern research on the foundations of quantum mechanics. Jones and Bartlett Learning. 2006.
- Tittel W, Brendel J, Zbinden H, Gisin N. Violation of Bell inequalities by photons more than 10 km apart. Phys Rev Lett. 1998;81(17):3563.
- Shih YH, Sergienko AV. A two-photon interference experiment using type II optical parametric down conversion. Phys Lett A. 1994;191(3-4):201-207.
- Hellmuth T, Walther H, Zajonc A, Schleich W. Delayed-choice experiments in quantum interference. Phys Rev A. 1987;35(6):2532.
[Crossref] [Google Scholar] [PubMed]
- Jacques V, Wu E, Grosshans F, Treussart F, Grangier P, Aspect FA, Roch JF. Delayed-choice test of quantum complementarity with interfering single photons. Phys Rev Lett. 2008;100(22):220402.
[Crossref] [Google Scholar] [PubMed]
- Ma XS, Kofler J, Zeilinger A. Delayed-choice gedanken experiments and their realizations. Rev Mod Phys. 2016;88(1):015005.
- Kuzmenko VA. On the experimental study of nonlocality in quantum physics. eprint, viXra. 1902.