About New Simple Interpretation of Trajectories of Particles with Various
Types of Spin

Alex; er VY

Short communication

, Volume: 6( 1)

About New Simple Interpretation of Trajectories of Particles with Various Types of Spin

Alexander VY^*

Department of Physics, University of Puschino, United States

*Correspondence:: Demetris Ghikas PK Department of Physics, University of Puschino, United States
Tel: +0306972268044; E-mail: ghikas@physics.upatras.gr.

Received Date: December 08, 2018 Accepted Date: April 07, 2018 Published Date: April 11, 2018

Citation:Alexander VY. About New Simple Interpretation of Trajectories of Particles with Various Types of Spin. J Phys Astron. 2018; 6(1):146

Abstract

The simple and evident scheme on the plane for geometrical interpretation of trajectories of particles with various types of spin is described. Trajectories corresponding to the movement of particles and antiparticles with half-integer, integer and zero values of spin are shown.

Keywords

Particles; Trajectories; Spin; Geometrization of physics

Short Communication

In quantum mechanics concepts of spin and isotopic spin T is widely applied [1,2]. Though spin and isotopic spin describe the different phenomena, their mathematical apparatus coincides. So we will use symbol s for any kind of spin as it is presented in monograph [1].

Particles possess integer (S=0,1) or half-integer (S=1/2) spin. So for example (S=1) for photons (S=1/2) for electrons, (S=1) and (S=0) for π-mezon and Σ-hyperon but (S=1/2) for nucleons, K-meson and Ξ-hyperon, etc [1,2].

Projections of isotopic spin on axis Z [1,2] can accept positive or negative values:

for half-integer spin or 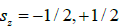equation (1)

for integer spin 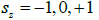equation (2)

It is considered that spin is the purely quantum mechanical concept, the certain "own" moment of a particle irrelevant to the movement of a particle in space and therefore the phenomenon of spin essentially doesn't allow classical interpretation [1,2].

In work the new evident geometrical model received on the basis of binomial distribution and consisting of broken lines and the branching trajectories inclined under small angles to an axis for the description laminar and turbulent movement of liquids in pipes has been offered [3].

In works the similar model has been offered for the evident description of the movement of electrons in atoms and explanations of atomic spectrum [4,5].

In work the possibility of application of the similar models consisting of broken, curved and branching trajectories in biology research is shown [6].

In work the geometrical model of the second shell of atom has been separately considered, communication of this model with the cubic equation and a formula of Cardano is shown, the special type of a triangle is described [4].

In works we have concerned geometrical interpretation of half-integer spin of electrons in the form of a trajectory and angles [4,5].

Process of consecutive geometrical construction by means of compasses and a ruler of shells and subshells of atom in the form of the wavy systems of trajectories it is shown in work [6,7].

In this work we will consider the simple and evident geometrical scheme for interpretation on the plane or projections to the plane it is similar to expressions (1, 2) trajectories of particles with various types of spin in more details.

In Figures 1-3, various systems of rays placed in a rectangular coordinate grid are shown. The size of a cell of a grid has height of k/2 and length of L, at the same time L>>k/2.

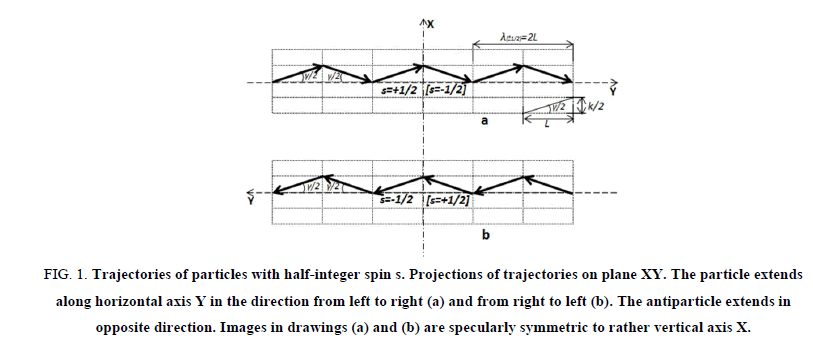
Figure 1:Trajectories of particles with half-integer spin s. Projections of trajectories on plane XY. The particle extends along horizontal axis Y in the direction from left to right (a) and from right to left (b). The antiparticle extends in opposite direction. Images in drawings (a) and (b) are specularly symmetric to rather vertical axis X.

Figure 2: Particles and antiparticles with half-integer spin s.

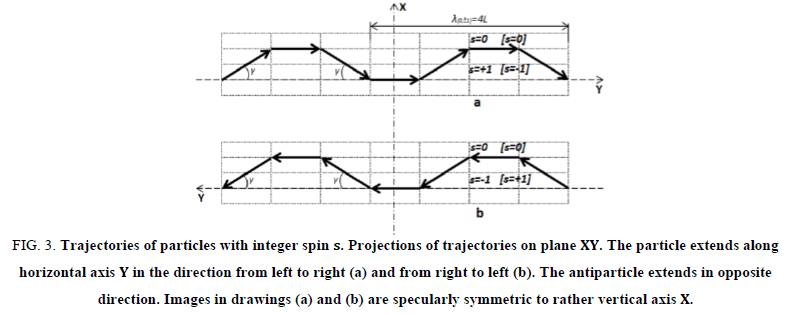
Figure 3: Trajectories of particles with integer spin . Projections of trajectories on plane XY. The particle extends along horizontal axis in the direction from left to right (a) and from right to left (b). The antiparticle extends in opposite direction. Images in drawings (a) and (b) are specularly symmetric to rather vertical axis .

In Figure 1 the system of rays corresponding to half-integer spin (1) is shown. Figure 1 it is similar to the image of the first shell of atom provided in Figure 1 in work (Yurkin, 2016 a). The wavelength of wavy trajectories shown in Figure 1 is:

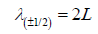equation (3)

The “waves” consist of two alternating links inclined at small angles γ/2 to axis Y of the direction of the movement. This scheme corresponds to the movement of a particle, with half-integer spin s=+1/2 in the direction of axis Y from left to right (a), and spin of a particle of s=-1/2 in the direction of axis Y from right to left (b). In this drawing is shown the value of spin (in square brackets) of antiparticle with half-integer spin [s=-1/2] the direction of axis Y from left to right (a), and spin of an antiparticle [s=+1/2] the direction of axis Y from right to left (b).

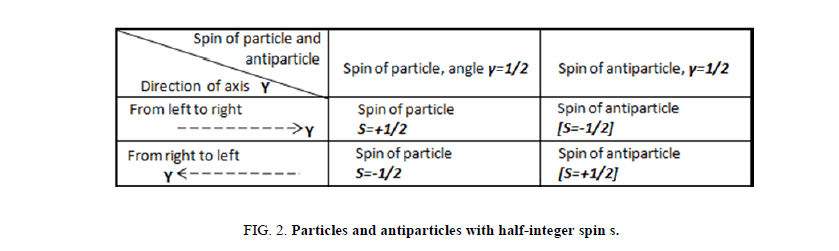
We tabulated in Figure 2 the results of our schematic creation of the movement of particles and antiparticles with half-integer spin:

In Figure 3 the system of rays corresponding to integer spin (2) is shown. The wavelength of wavy trajectories shown in Figure 3 is:

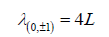equation (4)

The “wave” consists of four alternating links inclined at small angles γ to axis Y of the direction of the movement and two links parallel to axis Y (γ=0).

This scheme corresponds to the movement of a particle, with integer spin s=+1 in the direction of axis Y from left to right (a), and spin of a particle of s=-1 in the direction of axis Y from right to left (b). In this drawing is shown the value of spin (in square brackets) of antiparticle with integer spin [s=-1] the direction of axis Y from left to right (a), and spin of an antiparticle [s=+1] the direction of axis Y from right to left (b). This scheme also corresponds to the movement of a particle or antiparticle, with zero spin s=0 and [s=0] for links parallel to axis Y (a, b).

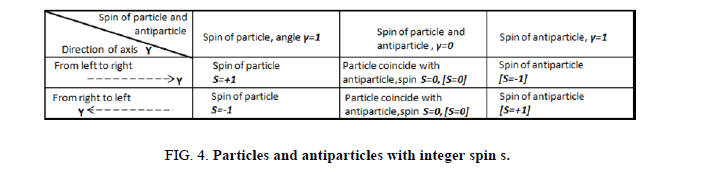
We tabulated in Figure 4 the results of our schematic creation of the movement of particles and antiparticles with integer spin:

Figure 4: Particles and antiparticles with integer spin s.

Certainly our simple geometrical constructions on the plane can describe only formally some properties of various elementary particles. Especially it belongs to particles with the integer spin. Perhaps, such particles as, for example, π-mezon [1,2] can during various periods of time prove as particles with single or zero spin. However our simple models demonstrate the difference of half-integer and integer spin. We hope that our geometrical interpretation of spin will help to understand more accurately and visually this natural phenomenon.

Acknowledgments

To S. Shnol, V. Mikhalevich, J. Peters and A. Tozzi for their interesting to this subject.

References

Landau LD, Livshits EM. Theoretical physics: Quantum mechanics. Nonrelativistic Theory. Moscow: Nauka. 1989; 3.
Savelyev V. Course of the General Physics. Moscow: Nauka. 1982;3.
Yurkin AV.Symmetric triangle of Pascal and arithmetic parallelepiped. On possibility of new evident geometrical interpretation of processes in long pipes. Lambert Academic Publishing. 2015.
Yurkin AV. ?n descriptive geometrical interpretation of the principle of Pauli, elements of the table of Mendeleyev and the Newtonian laminar current of liquid. Progress in Physics. 2016;12:149-69.
Yurkin AV. Silver ratios, Cardano’s formula and visual model of the second atomic shell. International Journal of Development Research. 2016;06:8077-84.
Yurkin AV. New, binomial model of atom, trajectories and schemes of energy of splitting levels of atom. IOSR Journal of Engineering. 2017;19-31.
Yurkin A, Tozzi A, Peters JF. Quantifying energetic dynamics in physical and biological systems through a simple geometric tool and geodetic curves. Progress in Biophysics and Molecular Biology. 2017;153-61.

Short communication