Current opinion

, Volume: 11( 1) DOI: DOI. 10.37532/2320-6756.2023.11 (1).319

• View PDF
• Download PDF

A Mathematical Relation Between Time And Entropy

*Correspondence:

Najmuj Sahadat Sarkar
Independent Researcher, Journal of Physics and Astronomy, India
E-mail: sarkarlimon794@gmail.com

Abstract

In this paper I show that time and entropy are mathematically related. As entropy increases, time will increase. A universe with less entropy would have less time. A universe with more entropy has more time. So the longer the time evolution of the universe or the older it is, the higher its entropy. Everything in nature is moving from order to disorder. Regularity or order is decreasing, and chaos is increasing. The entropy of the universe was at its lowest during the Big Bang. That is why the big bang stage is called the Highest Ordered stage. By applying some simple classical physics and thermodynamics we can derive a result for time and entropy. But initially I considered the photon particle at the edge of a black hole. The photon particle is located tangentially to the outer event horizon. Then through some quantum mechanical assumption i found that the subjects are mathematically related.

Keywords

Entropy; Time; Black Holes; Universe; Quantum Physics

Introduction

Suppose a particle or photon is at the edge of a black hole. By edge I mean it touches the Event Horizon. So that particular particle will feel a force by the black hole. The gravitational force will be so great that no one will be able to stop the particle from entering the event horizon. It then moves from the outer event horizon to the inner event horizon. We have already known about the black hole that the Inner event horizon is the world in which an object once entered cannot come out. Because to get out of there, he has to travel faster than the speed of light. Traveling faster than the speed of light means disobeying Einstein's theory of relativity. This is a very common concept. Now let's get back to some calculations.

First, we write the energy of a photon particle quantum mechanically as,

Here,

E=energy of photon.

h=Planck's constant.

ν=frequency.

Moreover, it is equal to v=c/λ. λ is the wavelength of the photon. Substituting this value into equation (1) we get,

The photon cone is tangent to the event horizon at a distance R from the center of the black hole. Now assume that the wavelength of the photon is somehow equal to R. We may enforce this Convention. Then,

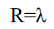
Again,

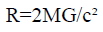
M is the mass of the black hole and c is "speed of light". Then equation (2) becomes,

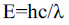
Or,

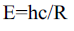
Or,

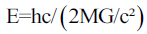
Or,

Also equal to E=mc². Since the presence of particles implies the presence of energy. So Substituting E=mc² into equation number three shows,

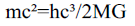
Or,

By a black hole of mass m, the gravitational force experienced by a photon particle of mass m will be,

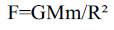
Or,

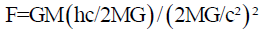
Or,

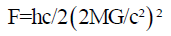
Or,

From Newtonian mechanics we know that force is again equal to mass times acceleration, (F=ma) so

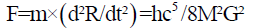
In this case m=hc/2MG, substituting this value in the above equation we get,

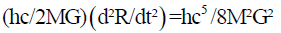
Or,

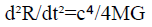
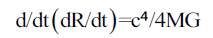
Or,

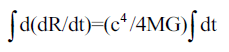
Or,

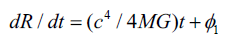
If you intrigue again, you will get,

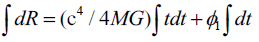
Or,

If the boundary condition is applied, then we get Φ₁=Φ₂=0. In this case Φ₁, Φ₂ are acting as constants. Then equation (6) becomes,

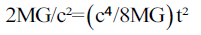
Or,

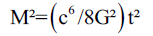
Or,

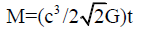
Or,

From Hawking Temperature we know,

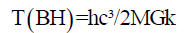
Or,

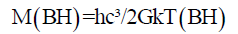
Substituting this value of M into equation (7), we get

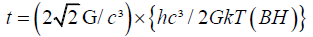
Or,

Moreover, earlier I proved that the temperature of a black hole is exponentially proportional to the square root of its entropy. Therefore,

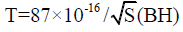
Substituting this value of T into equation (8), we get,

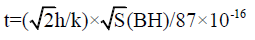
Or,

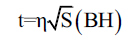
Or,

In this case

Here t is the time it takes for a photon to enter a black hole with entropy S (BH). 2 photons will take 2t, time to enter. 3 photons will take 3t, time to enter. Thus n photons will take not time to enter. We can say that as more photons enter the black hole one by one, its entropy starts to increase. Moreover, the time taken by n number of photons to enter the black hole can be represented by τ. That is:

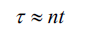
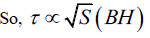
Black hole itself is a thermodynamic system. So as time increases its entropy will increase. The same is true for our universe. According to the second law of thermodynamics, we observe the unidirectional flow of time in nature because the entropy of the universe is increasing. My equation is dimensionally consistent. If I assume that at the beginning the entropy of the universe was 0, then time would have no meaning. Since then time will be 0. So it would be foolish to think about physical space. And this is directly or indirectly pointing to the singularity. Time and entropy are mathematically related. A graph of entropy versus time will depict a straight line.