Research
, Volume: 10( 1) DOI: 10.37532/2320-6756.2022.10(1).256A Light Deflection due to Forcing a Light Beam Hogged in Passing by the Sun in the Cartesian Coordinate System
Received: November 21, 2021, Manuscript No. M- 47974; Editor assigned: November 25, 2021,PreQC No. P 47974; Reviewed:December 17, 2021, QC No. 47974; Revised: December 25, 2021, Manuscript No. R-47974; Published: January 3, 2022, DOI: 10.37532/2320-6756.2022.10(1).256
Citation:Yasutsugu Ohki, A light deflection due to forcing a light beam hogged in passing by the Sun in the Cartesian coordinate system, J Phys Astron.2022;10(1):256.
Abstract
This paper proposes a new theory, given a beam reflected on a surface of the Mercury, to force the beam to hog in passing by the Sun. Under Maxwell’s exact differential equations, the theory is derived from postulations: (i) Every beam has multiple properties of mass density, momentum, energy, power, force. (ii) Every source of the beam radiates concurrently a mobile self-medium and the beam. (iii) The medium has a uniformity with isotropy, homogeneity, and partial differentiable continuity. (iv) The medium helps the electromagnetic field generate in itself. (v) The beam has an intrinsic repulsive force product of a time derivative of electric flux density and magnetic flux density. (vi) When a beam collides with the other beam at a right angle, a lifting force for the beam collided has a direction acting as an adverse effect in the conventional catenary theory. (vii) The catenary theory gets a constant negative β defined as a ratio of the lifting force to the repulsive force. (viii) From approximation of the catenary theory, the hogged angle Δθ (hog) changes (1/2) βX I (rad), where β is four divided by the speed of beam squared and X is an adequate distance forced to hog. Consequently, the angle Δθ (hog) results in nearly coincident with the well-known angle, Δθ=(1.75γ/2)/(d/Rs)[rad], where d is a distance between a surface of the Sun and the Mercury located at the perihelion point of the Mercury and Rs (a radius of the Sun), γ (a coefficient in a radian unit).
Keywords
Deflection of light; Electromagnetic wave-corpuscular beam; Kepler’s equation; Maxwell’s equations; Exact differential equation
Introduction
As for Einstein’s theory of deflection of light passing by the sun due to gravitational effect [1-4], his theory has prevailed up to the present time so that the theory has been backed up by facts [5]. However, his theory does not deny an unknown theory of the others. In addition, most people believe that light has massless or no-mass not to violate the Lorentz transformation [6]. First, this paper alleges that a one-dimensional electromagnetic light beam has multiple properties of mass, energy, energy, force, the power so that the properties is derived from a combination of Maxwell’s equations and exact differential equation (Maxwell’s exact differential equations, Medes, hereafter) in the Cartesian coordinate system. Second, the conventional concept of light has been imaged light with no mass, or massless; this paper proposes the concept should sweep away, so this paper uses the speed of beam as a replacement of the speed of light here after. We know that, through equation (C-7a) in Appendix C and equations in Appendix A, one dimensional scalar electromagnetic energy density ρ(E) on z-axis is expressed [7].
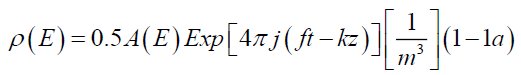
where,
f: a discrete frequency [1/s]
t: time variable, or time interval variable Δt[s]
k: wave number [1/m]
z: space variable on an axis for the beam to travel, or space interval variable Δz[m]
Exp: Euler’s formula [8]
j: imaginary unit [9]
Cube: A function cubed
A(E): Amplitude of wave function of electromagnetic energy
0.5=1/2: coefficient squared due to multiplying two terms with root mean squared
Third, in multiplying both hands in equation (1-1a) by electromagnetic constant εμ product of permittivity ε and permeability μ in vacuum space, we can get one-dimensional electromagnetic mass density ρ(m) defined as below.
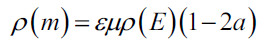
This equation makes up only electromagnetic terms, integrating both hands in equation (1-2a), we can get a famous equation that mass equal to energy divided by the speed of beam squared.

The above equation (1-2b) means that an electromagnetic mass of the beam can transfer electromagnetic energy, in reverse, the energy can transfer the mass of the beam. Therefore, the electromagnetic mass in the above equation do not mean the mass of the particle [10]. Furthermore, we know electromagnetic energy is described as energy waveform [11], from equation (1-2a), multiplying both hands in equation (1-1) by electromagnetic constant εμ, so an electromagnetic mass of the beam can describe below.
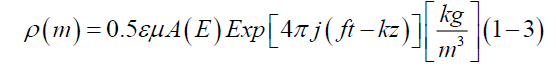
The equation shows the wave-beam with mass duality in the form of root mead squared so that we can define one-dimensional electromagnetic momentum density ρ(M) as a term product of the electromagnetic mass density and the speed of the beam, derived from Maxwell’s exact differential equations in detail hereafter.
Fourth, under a thought experiment, the beam can cut up itself, however, the speed of the beam per unit of second is a length of an element of the beam for all of the beams assemble at every node over full-spectrum. This expression of the wave-beam duality corresponds to the wave-particle duality [12 ]. However, according to the above statement, the beam cannot regard as a particle, for the beam is a continuous entity unable to cut up itself for the indeterminacy of the beam [13]. Consequently, the above-statement of the wave-beam duality will cast aside most people espoused the wave-particle duality in particle mechanics [14].
Now, returned to this paper’s subject, as for the other momentum and volumetric mass density, this paper can develop an argument of a new theory of the deflection of light. In the Cartesian coordinate system [15], when given electric flux density vector D with a discrete frequency and magnetic flux density vector B with the same frequency, wavenumber, and zero phase angle, momentum volumetric density vector of the beam is defined as one-dimensional electromagnetic momentum vector integrating from the minimum frequency to the maximum with respect to the frequency variable over full-spectrum.
So, using equation (C-1) in Appendix C, a one-dimensional electromagnetic momentum density beam vector with a discrete frequency is expressed,
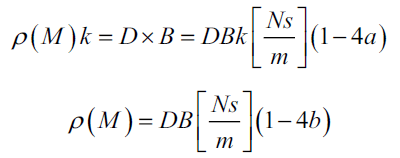
where k is unit vector on z-axis in the coordinate. Hereafter, the above vector sign rules out, so a scalar beam momentum density ρ(M) used for the beam vector is only on the z-axis.
Next, as the inevitable thought that an electromagnetic beam needs an electromagnetic field, in general, we have to postulate a selfmedium that allows the beam to generate a field. This self-medium is assumed to be due to two types: an immobile and mobile medium.
On the other hand, we know that the immobile medium was denied with the experiment by Michelson-Morley [16 ], so the other is postulated as a mobile self-medium radiated from its source by Ohki [17]. In reference to Appendix B, the mobile self-medium has a property of electromagnetic permittivity and permeability in vacuum space and travels at the speed of beam equal to the square-rooted reciprocal product of the permittivity and permeability derived from the Medes.
Therefore, using the self-medium, the beam can travel concurrently with the self-medium at the speed of the beam in a vacuum space with no media. According to the above statement, the beam density has a property of one-dimensional continuity of momentum, energy mass density in vacuum space with uniformity [18] in the self-medium.
Besides, in reference to equations in Appendix C, we can get equations:
(a) A scaler electromagnetic momentum ρ(M) in equation (C-2)
(b) A scaler electromagnetic energy ρ(E) multiplying the beam by electromagnetic constant εμ in equation (C-10),
(c) A scaler electromagnetic mass density ρ(m) divided by the speed of beam in equation (C-9) .
It follows that the continuous beam has a property unable to cut up an element at any place except for each node for all waves of the beam to concentrate at a space interval of the speed of beam per unit of the second over full-spectrum in the Cartesian coordinate system.
Note. This above-stated beam system regarded as a continuous entity fundamentally perfectly conflicts with a particle in Newtonian mechanics [19].
Postulations
To get a new deflection theory in the Cartesian coordinate system, referring to Appendix, and to argue cogently in detail, we need to have postulations:
(P1) A one-dimensional Maxwell’s exact differential equations (Medes)
Each term is adaptable to the Medes defined as a combination of the Maxwell’s equations and exact differential equation in the Cartesian or rectangular coordinate system.
(P-2) A mobile self-medium
A mobile self-media has a property of a physical and mathematical perfect uniformity with respect to space variable z and time t, or space interval and time interval variable, and of constant permittivity and permeability to make electromagnetic field the Cartesian coordinate system.
(P-3) A one-dimensional electromagnetic wave-beam duality
Under conditions that each beam is in the self-medium, each property of the beam, theoretically derived from the Medes, and has a dual property of wave and a corpuscular beam, so the beam characterizes electromagnetic volumetric density of mass, momenta, energy, power, and force, respectively, besides, they are expressed as a wave function.
(P-4) A source of the beam
A source of the beam is subtended with the self-medium with permittivity and permeability in a vacuum space. It allows the beam to travel at the speed of beam, square-rooted equal to the reciprocal electromagnetic constant product of permittivity and permeability. Therefore, the beam and the self-medium can concurrently radiate at the speed of the beam under no acceleration from the same source. So the self-medium can help the beam travel at the speed of the beam even in a vacuum space.
(P-5) Every node of waves of the beam
Each wave in the beam has a node at a length of 1[m] and of c[m] the speed of beam c per unit of second, respectively, so a location of the node seems to be the prime number, and we can observe wave energy unit separated with a prime number. We cannot observe an element of the beam just at a node for the beam to ensemble, so we can observe a truncated beam with some existence probability.
(P-6) The self-medium with uniformity
According to the uniformity mentioned above, a one dimensional derivative of space interval variable Δz with respect to time interval variable Δt, that is, dz/dt or Δz/Δt rate of space interval to time interval, comes to be a universal speed in all directions so that we can call the speed of beam in a vacuum space in all directions [20].
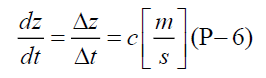
Where, c is the speed of beam.
(P-7) Reciprocal of time interval and space interval
The reciprocals of time interval and space interval, respectively, are equivalent to frequency, reciprocal of no-zero time interval and wave number, reciprocal of no-zero space interval in the wave function.
(P-8) The beam bisecting two beams at a right angle
In case that the beam radiated from a source bisects two beams: A beam directly radiated from a surface of the source, and the other beam reflected from a reflecting surface irradiated from the source. They interfere as wave property and interact with each other as the corpuscular property in the duality.
(P-9) Momenta due to Completely-elastic collision between two beams bisected
In the case of two beams bisecting at a right angle, they make the momenta multiplied by two as an effect of perfect connection of the beam at a collision cross-section area of A. On the other hand, the direct beam has a volume multiplying the area A by the speed of beam per unit of the second.
(P-10) Lifting force per unit of length
According to equation (D-1a) and (D-1b) in appendix D, a lifting force density is expressed.
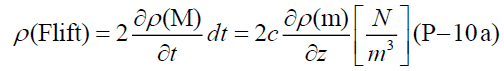
where, 2 is the coefficient in the case of a completely-elastic collision between the beam reflected from the Mercury and the beam directly radiated from the Sun.
(P-11) Spatial current density
Replacing the displacement current density defined by James Clerk Maxwell [21] with spatial current density newly defined in this paper for no existence displacing the media in vacuum space, and he thought of it as the luminiferous medium [22-24]. Using new definition of scalar spatial current density in equation (B-3) in Appendix B, one dimensional scalar intrinsic repulsive force is expressed.
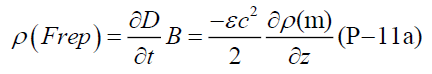
One dimensional repulsive force density vector is defined as one product of the spatial current density in equation (P-11a) and magnetic flux density B, using equation (P-11a), (B-5e), (B-6b), and (P-6a), under constancy of permittivity and the speed of the beam in vacuum space, so we can get scalar repulsive force density.
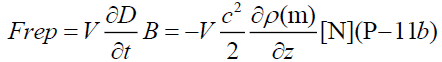
In consequence, β is defined ratio of the lifting force to the repulsive force, using equation (P-10a), (P-11a), and V= Ac in equation (E-1), we can get a constant β.
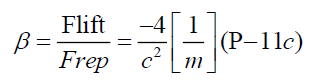
Precaution statement: In an equation (P-11c), unit of the lifting force density ρ(Flift) is Newton per unit of area and unit of the repulsive force is Newton per unit of volume per unit of second, so that unit of ratio β is per unit of length, though we can seem the unit of the reciprocal of the speed of beam squared.
(P-12) Catenary theory with constant negative β
In referring to appendix E, though the conventional catenary theory has a constant positive for gravitational attractive force, in reverse, this paper proposes a new catenary theory has constant negative β for the lifting force works the beam. The catenary theory, using approximate expression under conditions that the constant is very small, is expressed as a quadratic equation, so the lifting effect is described as a versine hog [25-27].
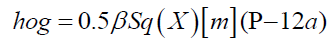
Next, using approximate expression under conditions that a tangent angle is minimal, the tangent angle at a surface of the Sun is,
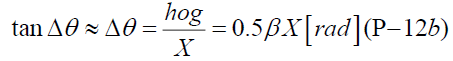
Using the above equation and (P-11c), we can get an equation of the deflection of light passing by the Sun below:
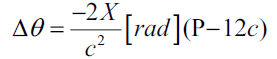
where,
X: A distance subject to a hogging effect due to an interaction between a beam directly radiated from the sun and the other beam reflected from the Mercury.
Δθ: A tangential angle between a beam stymied by the Sun and a visible hogged beam deflected by the interaction between the other beam
Orbit Theory and Assumptions
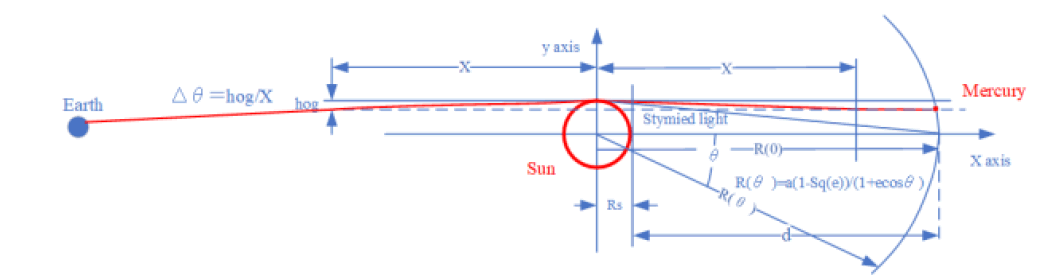
In reference to FIG. 1, to estimate the deflection of the beam, we need to have assumptions below.
Figure 1: Orbit theory and a deflection of the light reflected on the Mercury due to the catenary with constant negative.
(A-1) When the Mercury obeys the orbit theory [28-31], so the perigee radius R is,
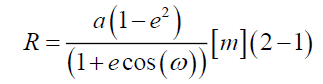
where,
a: a is the semimajor axis of the ellipse [m]
e: e is the orbital eccentricity
ω: The true anomaly [rad]
(A-2) The focus of the Sun is immobile
(A-3) Table 1 offers all data to estimate the deflection of beam
(A-4) A tangential angle equation about the deflection of light [32,33] is
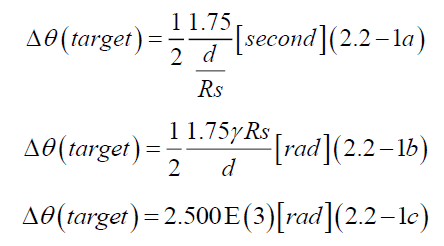
where,
Δθ (target): A one of the deflection equations
γ: A factor of conversion of a radian into a second [26]; a radian [rad] is(180×3600/π) second [second]
Rs: Radius of the Sun [m]
R(0): perihelion distance between a point of perihelion of the Mercury and the point of focus of the Sun
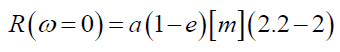
d: a distance subtracted the radius from the perihelion, a point far away a surface of the Sun
E(3): Engineering notation, equal to 1000 [34-36]
Digit number of significant figures to estimate is subject to 4 digits for equation (2.2-1a) Using constant negative β in equation (P- 11c), if the hogging distance in equation (P-12c) is assumed as X =1.124 E(9)[m], using data in Table. 1, we can get a value in equation (P-12c).
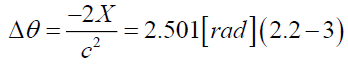
| No. | Definitions | Sign | Value | Unit | Reference |
|---|---|---|---|---|---|
| 1 | Semimajor axis | a= | 1.496 E (11) | m | Note 2 |
| 2 | Radius of the Sun | Rs= | 6.963 E (8) | m | Note 2 |
| 3 | Perihelion of the Mercury | R (θ = 0) = R (0) = | 4.600 E (9) | m | [37] |
| 4 | Orbit eccentricity of the Mercury | e = | 0.256 | Note 2 | |
| 5 | A distance far away from the Sun | d = R (0)-Rs = | 1.181 E (11) | m | Note 2 |
| 6 | The speed of beam | c = | 2.998 E (8) | m/s | Note 2 |
| 7 | Temperature at the surface of the Sun | Ts = | 5.778 E (3) | K | [38] |
| 8 | A hogging distance of the interaction | X= | 5.778 E (3) | Note 3 | |
| Note1. E(N) is engineering notation [37], 10 to the Nth power | |||||
| Note2. Mercury/Earth Comparison data [38] | |||||
| Note 3. A hogging distance of the interaction between the direct beam and reflected beam is assumed 1.124 E (9) [m] | |||||
TABLE. 1 Estimation under controlling number 4 digits of significant figures on the engineering notation
Conclusion
We can accomplish our goal that Δθ in equation (2.2-2) is estimated to be nearly equal to Δθ (target) in equation (2.2-1c) under postulations and assumptions:
(a) A mobile self-medium radiated at the speed of beam, that is, the so-called speed of light from a source of beams
(b)The self-medium has a uniformity with isotropy, homogeneity, and continuity partial differentiable in the Cartesian coordinate system
(c) The beam has an intrinsic repulsive force due to a product of spatial current density vector and magnetic flux density vector in the self-medium
(d) The lifting force is due to an interaction between a beam with a lateral side of collision cross-section and a beam normal to the lateral.
The other fruitages except for the above fruitage are detailed:
(A) Time going beyond creed of light with massless
Most people who study Maxwell’s equations know electromagnetic-energy density ρ(E), that is,
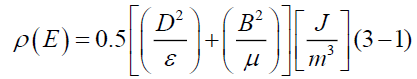
So, through multiplying this equation by electromagnetic constant εμ, we can get simply electromagnetic-mass density ρ(m), that is,
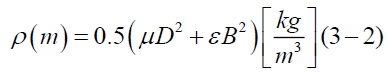
Besides, we can obtain each equation of ρ(E) with the amplitude A(E) and ρ(m)with A(m), in waveform, respectively,
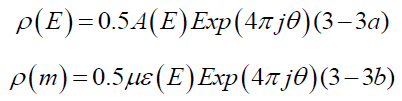
Those above-equations will imply that the belief of light massless or no mass should dig the grave, and the wave-beam duality will supersede a term of the wave-particle duality.
Furthermore, we know the Lorentz factor β, 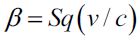 in the Lorentz transformation with particle’s speed v, using
in the Lorentz transformation with particle’s speed v, using 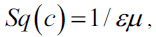 , we can get the Lorentz factor
, we can get the Lorentz factor  . From this expression of
. From this expression of 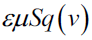 , we will be unable to image that rest mass become to be infinite. The above-statement urges to stop regarding light as a particle with mass, and using the speed of beam in the Lorentz transformation. Furthermore, the speed of beam will supersede the term of the speed of light.
, we will be unable to image that rest mass become to be infinite. The above-statement urges to stop regarding light as a particle with mass, and using the speed of beam in the Lorentz transformation. Furthermore, the speed of beam will supersede the term of the speed of light.
(B) The multiple forms
Equations in Appendix C show waveforms of mass, momentum, and energy.
In addition, using the well-known electromagnetic energy density product of the Planck constant and a discrete frequency [28],
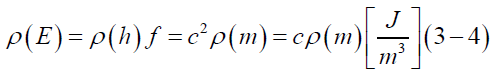
where,
h: the Planck constant
V: A beam’s volume
ρ (h): Ratio of the Planck constant divided by the volume, as a meaningless expression
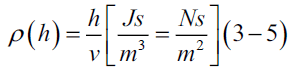
Next, integrating equation (3-4) to a volume V of the beam, we can get a relationship between electromagnetic mass m, momentum M and the Planck energy product of the Planck constant h and a discrete frequency f [29].
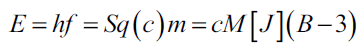
(C) Continuity of the beam
The above statement that all waves concentrate a node of a distance of the speed of beam per unit of second, so that we cannot observe just a set distance of the node. So, if forcing the set truncating, the observation data of the beam will have a probability distribution for cutting up the set of the beam, which will be corresponding to the Born rule [30]. In consequence, in thought experiments, we can get a wave element with discrete frequency in the beam and a node unit. However, we cannot observe an element of the beam, a single photon just at a node of the beam, and a discrete frequency, subject to the indeterminacy.
(D) Indetermination of the beam subject to time interval and space interval
We have no choice to observe a truncating element of the beam, so that the beam has an observation distribution. In consequence, we have no choice to face an indeterminacy of the beam.
(E) Interaction between beams in the same self-medium
This equation of
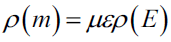
implies mutual conversion between electromagnetic mass and energy. We can show the pieces of evidence:
(1) We know those facts that electromagnetic beam generates in annihilating due to collision of an electron and a positron with each high speed [31].
(2) When an electromagnetic beam attains high energy conditions in colliding with each other, so the beam changes into an electron or electrons from the energy [32].
(3) Furthermore, a proposal concept that an electron makes up three beams by Ohki, is derived a relationship between classical electron radius and electron mass [33,34] under conditions that an electron has a perfect cubic figure with the radius. The facts and the proposal imply that we can postulate an interaction of the high power beams radiated from the Sun.
References
- Roy S, Sen AK. Study of gravitational deflection of light ray. In J Phys Conf Ser. 2019:1330(1);012002.
- Will CM. The renaissance of general relativity. New phys. 1989:7-33.
[Google Scholar] [Crossref]
- On one of the fundamental consequences of general relativity: the deflection of light by gravity
[Google Scholar] [Crossref]
- Kennefick D. Traveling at the Speed of Thought. Princeton univ press. 2016.
[Google Scholar] [Crossref]
- Gravitational lens 2021
[Google Scholar][Crossref]
- Stuart B. Palmer and Mircea S. Rogalski, Advanced University Physics, Gordon and Breach Publishers, 1996; 68.
[Google Scholar] [Crossref]
- Amnon Yariv, Optical Electronics, Fourth Edition, Harcourt Brace Jovanovich college Publishers, 1991:7.
[Google Scholar] [Crossref]
- Euler’s formula, C Ray Wylie and Louis C. Barrett, Advanced Engineering Mathematics, McGraw-Hill Book Company, 1982:892.
[Google Scholar] [Crossref]
- Imaginary unit, Wikipedia, https://en.wikipedia.org/wiki/Imaginary_unit. 2021.
[Google Scholar] [Crossref]
- Particle -Wikipedia, https://en.wikipedia.org/wiki/Particle . 2021
[Google Scholar] [Crossref]
- Amnon Yariv, ditto. 2010:7.
[Google Scholar] [Crossref]
- Wave-particle dualityhttps://en.wikipedia.org/wiki/Wave%E2%80%93 particle_duality 2021
[Google Scholar] [Crossref]
- Ohki Yasutsugu, Authentic Fermat' s principle on the basis of a closed circuit looped optically with electromagnetic progressive and retrogressive path.
[Google Scholar] [Crossref]
- Stuart B. Palmer and Mircea S. Rogalski, Electromagnetic wave-mass density duality derived from exact differential equations in one-dimensional Maxwell's equations in orthogonal space, 2019:1-12.
[Google Scholar] [Crossref]
- Cartesian coordinate system, https://en.wikipedia.org/wiki/Cartesian_coordinate_sy stem. 2021.
[Google Scholar] [Crossref]
- The Michelson-Morley experiment Wikipedia,https://en.wikipedia.org/wiki/Michelson%E2%80%93 Morley_experiment 2021
[Google Scholar] [Crossref]
- Ohki Yasutsugu, "The Inherent Derivations Derived Theoretically from One-Dimensional Maxwell’s Equations on the Basis of Exact Differential Equation",2020:1-7.
[Google Scholar] [Crossref]
- Ohki Yasutsugu, Universal physical constants derived from each of uniformity systems in space and time. 2021.
[Google Scholar] [Crossref]
- Stuart B. Palmer and Mircea S. Rogalski, ditto, 12.
[Google Scholar] [Crossref]
- Ohki Yasutsugu, Universal physical constants derived from each of uniformity systems in space and time.
[Google Scholar] [Crossref]
- James Clerk Maxwell, “Electricity and Magnetism”, Dover Publications, Inc. 1891:2;439.
[Google Scholar] [Crossref]
- Versine Wikipedia, https://en.wikipedia.org/wiki/Versine,2021.
[Google Scholar] [Crossref]
- Orbital Mechanics-Wikipedia, https://en.wikipedia.org/wiki/Orbital_mechanics, 2021.
[Google Scholar] [Crossref]
- Clifford Will, “The New Physics edited by Paul Davies, The renaissance of general relativity.”, Cambridge University Press, 1989:7-33.
[Google Scholar] [Crossref]
- Cohen ER, Giacomo P. Symbols, units, nomenclature and fundamental constants in physics. Amst N Holl. 1987.
[Google Scholar] [Crossref]
- Ohki, “Derivation of an electron composition theoretically from one-dimensional Maxwell's exact differential equations”, May 2019, https://www.researchgate.net/profile/Yasutsugu-Ohki.
[Google Scholar] [Crossref]
- Mercury/Earth Comparison, https://nssdc.gsfc.nasa.gov/planetary/factsheet/mercur yfact.html.
[Google Scholar] [Crossref]
- Classical electron radius, https://en.wikipedia.org/wiki/Classical_electron_radiu s. 2021.
[Google Scholar] [Crossref]
- Chase M. Discussions on the Eternity of the World in Antiquity and Contemporary Cosmology. Philos stud antiq class tradit. 2013:7(1);20-68.
[Google Scholar] [Crossref]
- Múnera HA. From the classical ethers of Descartes and Newton to cosmons and sagions. Apeiron. 2015:20(2);1-67.
[Google Scholar] [Crossref]
- Engineering Notation,https://en.wikipedia.org/wiki/Engineering_notation
[Google Scholar] [Crossref]
- Mercury/Earth Comparison, https://nssdc.gsfc.nasa.gov/planetary/factsheet/mercur yfact.html.
[Google Scholar] [Crossref]
- The Born rule, https://en.wikipedia.org/wiki/Born_rule. 2021.
[Google Scholar] [Crossref]
- Electron-positron annihilation, https://en.wikipedia.org/wiki/Electron%E2%80%93po sitron_annihilation, 8
[Google Scholar] [Crossref]
- HS Fu, MJ Zhao, Y Yu, et al. “A New Theory for Energetic Electron Generation Behind Dipolarization Front”, Geophys Res Lett. 2020.
[Google Scholar] [Crossref]
- Engineering notation, https://en.wikipedia.org/wiki/Engineering_notation, 2021.
[Google Scholar] [Crossref]
- Sun, https://en.wikipedia.org/wiki/Sun
[Google Scholar] [Crossref]