Viewpoint

, Volume: 11( 1) DOI: 10.37532/2320-6756.2023.11(1).318

• View PDF
• Download PDF

A Different Mass-Luminosity Relation for Black Holes

*Correspondence:

Najmuj Sahadat Sarkar
Independent Researcher, Journal of Physics and Astronomy, India
E-mail: sarkarlimon794@gmail.com

Abstract

I basically showed in this paper that the luminosity of a black hole is inversely proportional to the square of its mass. By applying some simple math we can relate mathematical properties to each other very easily. My paper says that the lower the mass of the black hole, the higher its luminosity. This mass-luminosity relation is completely different from the Eddington mass-luminosity relation. This means that if a black hole has less mass, its luminosity will be higher. But if the mass of the black hole is more, its luminosity will be less. I explained it this way, in the case of a low mass black hole, most of its mass is converted into energy. For which its mass is less. So its luminosity is high, and it’s also the reason of low surface area. But in case of black hole with more mass, its surface area will be more. So with more surface area, it becomes more likely that more anti-matter will enter there through Quantum Fluctuations. And it will reduce its mass energy density. If the mass density decreases, the mass will decrease. For which he will not get sufficient mass, so that he can eject an intense radiation.

Keywords

Black holes; Mass; Luminosity; Temperature; Energy; Supernova

Introduction

Black holes are one of nature's strangest objects. At the end of its life, a star explodes in a supernova, releasing all its material into space. But the stars don't end there. The core of the star still remains. After a supernova explosion, if a white dwarf star has a mass greater than 1.4 solar masses, the neutron degeneracy pressure cannot prevent the star's gravitational contraction. The star continues to contract. At some point it reaches the boundary line which is called event horizon. That is, the star turns into a black hole. It is impossible to predict what is happening inside the event horizon. This event horizon separates the black hole from our world. Any object that enters the event horizon is cut off from the outside world. Once an object enters the event horizon, it can never re-exit through it. Because to do that, matter has to travel faster than the speed of light. However, any object beyond the event horizon of a black hole can easily travel away from light or even at speeds less than light. But somehow, once light enters the Horizon, it cannot escape the black hole's gravity. At the center of the black hole is a singularity, where gravity becomes infinite, since then r=0. Space and time have no meaning in singularity. A disc of ionized gas is observed around the black hole, called the "accretion disc". Along this disc, the black hole swallows other stellar objects. As the mass of the black hole increases, its volume also increases. As the mass of the black hole increases, the temperature decreases. According to my calculations, it appears that black holes that are more luminous have less mass. That means most of their mass is being ejected as energy. And it is quite luminous. But those black holes which are less luminescent, have comparatively more mass. That is, a very small part of the mass, they are ejecting as energy. For which they are not very luminous. Moreover, black holes that have lower temperatures have significantly larger masses. But those whose temperature is high, their mass is low. We can define the temperature of an object as the amount of heat contained in that object. Now heat is energy. And its square is proportional to the luminosity of the black hole. Besides, it is known from Benkenstein formula that entropy and surface area of black hole are proportional to each other. The greater the surface area of the black hole, the greater its entropy. There is only so much chaos in it. In my mathematical theory, I first imagined a light wave, where the wave length is equal to the radius of the black hole. This radius is equal to the Schwarzschild radius. This particular radius represents the minimum size a black hole can grow. Then I put this radius, E=hc/λ in place of λ. So that I can get the energy expression. And that's pretty elegant. Now in thermodynamics we can write energy as "temperature" times "entropy change". But the entropy change for a photon particle entering a black hole can be captured by one unit. Since that means only one photon (for that one bit of information is enough). Entropy also plays a special role in Quantum Mechanics or Thermal Physics. In that case, energy and temperature will be same or equal. So I wrote it in Temperature expression instead of Energy expression. Then to calculate the black hole luminosity, I applied the Stefan Boltzmann formula (but only for Schwarzschild black holes) where the squared value of R(s) is substituted for the square of the radius. And the value of "T=hc³/2MG" is put in place of temperature. Finally I noticed a mathematical relationship between Luminosity and Mass. From the Planck relation or Planck-Einstein relation, we more or less learned that; The energy of a photon can be described by this formula: E=hv Or, E=hc/λ. As, ν=c/λ. Here, ν=Frequency of the light (photon), h=Planck constant, c= Speed of light. Let’s considered, the radius of the Black hole, equals to the wavelength of the photon that falls into the black hole, and one photon has one unit of entropy. So, R(s)=λ, R(s) is the minimum radius of the black hole of mass M. Now put this special case into the equation E=hc/λ, so we will get;

And what is R(s)?

Its the Schwarzschild radius of black hole, where R(s) equals to; R(s)=2MG/c ; Put this R(s) value in the equation 1, we might be get;

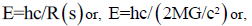
From Thermodynamics we know this Fact that, change in energy (dE) is proportional to "T ds" here ds is the change in Entropy. T is just the Temperature. So, if we relate this things mathematically to each other we will get this below relationship.

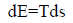
or we can rewrite it this way,

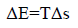
For a unit photon Δs=1(Δs just equals to 1). Δs is associated with Photon that falls into the black hole. Now we make an assumption; E or energy relate with Temperature "T". They are just proportional to each-other. That means if there is more temperature, there is more heat, or roughly speaking there is more energy. So, E~T (When Δs=1) if we want to relate with Equation 2, then the whole expression might be;

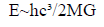
or,

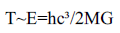
or,

Black holes are also like stars. They have Temperature, Mass, Spin, Gravity, Radiation, and all the crazy stuffs that a star needed. Black holes eject light or electromagnetic radiation in the form of Quasars. A quasar is an extremely luminous active galactic nucleus, powered by a black hole, with mass ranging from millions to tens of billions of solar masses, surrounded by a gaseous accretion disc. Probably the disc made by a vast amount of photon Gases. Gas in the disc falling towards the black hole heats up because of friction and releases energy in the form of electromagnetic radiation. So, they have certain Luminosity. Now we apply Stefan-Boltzmann law for a Schwarzschild black hole luminosity. If this law is applicable for stars, then it also applicable for black holes. More over black holes are made when a star run out of its nuclear fuel, and collapses due to the effect of gravity. The law is:-

Here, L(B×H)=Luminosity of the black hole.

σ=Stefan-Boltzmann Constant.

T=Temperature Of the black hole.

R(s)=Schwarzschild radius.

Now, R(s)=2MG/c²

And, T=hc³/2MG

Putting this two value in the equation 4, we must get:

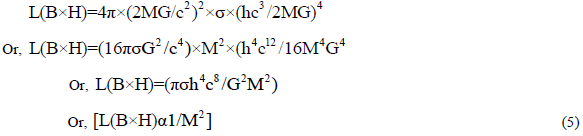
So, the luminosity of a black hole inversely proportional to the square of its mass. That means if a black hole is massive, then it is less luminous. But if the black hole has less mass then it is much luminous. Moreover, Temperature is inversely proportional to the Mass (M). So,

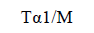
If we relate this expression with "equation 5", then we will get;

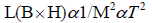
or,

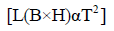
The above equation shows, if the black hole has less temperature, then it also has less luminosity, but if the black hole has much temperature then it has a vast amount of luminosity. By the way, what is the definition of temperature? Temperature is the amount of heat that stored in an object. Heat is energy. So the more luminous a black is, the more energy it has. Black holes have Luminosity which inversely proportional to its mass square.