Original Article

, Volume: 5( 4)

• View PDF
• Download PDF

On the Fractal Structure of Space-Time

*Correspondence:

Martinez A Texas A&M University, Department of Engineering, United States of America, Tel: +972 1-800-660-660; E-mail: allvaromartinez@gmail.com

Abstract

We show that strings are not one-dimensional objects and that they can be continously stretched to become 2-branes. This in turn suggests that strings have fractal structure. We then proceed to analyze curvature variations inside black holes, which after making use of their entropy properties and applying them a classical theorem in Riemannian Geometry, leads us to conclude that space-time is indistinguishable from energy. By considering the string’s structure mentioned above, this implies that space-time itself has fractal structure. Applications of such results include a solution of the problem regarding the universe’s shape by defining it as finite in size and with zero global curvature, and an explanation of high-temperature superconductivity by means of 2-branes’ stickiness property.

Keywords

Strings; D-branes; De sitter space; Black holes; Fractals; Soul theorem

Introduction

String Theory is a work under progress aiming to unify Quantum Mechanics and General Relativity into a single framework. Its main claims in order to achieve this are that all particles are one-dimensional vibrating objects called strings and that space-time has more than four dimensions. The theory also contemplates objects called D-branes (where D is their dimension), which are higher dimensional generalizations of strings. However, the structure of strings and of space-time at the Planck length is still not completely understood. The present paper studies both the detailed geometry of strings and of space-time by making use of their tension property and of black holes’ information strorage properties respectively.

It is thought that strings are one-dimensional vibrating objects which have tension. Yet tension, which consists on stretching an object, cannot take place in objects without width. Therefore strings are not one-dimensional and must have a certain degree of width in order to be stretched. As the tension of the string increases, it will inevitably increase in width up to the point where the string turns into a 2-brane. Therefore strings and 2-branes are equivalent and are fractals as well. This is because the string gains width in a gradual manner, thus assuming dimensions in the interval [1,2] in the process. Such conclusion is backed up by considering the string’s equation for tension,

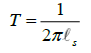
which cannot vanish since this would imply that the string has infinite energy. T being equal to zero would mean that the string cannot be stretched and is thus one-dimensional. Yet as one considers an arbitrarily small value for T, the string cannot pass abruptly from being almost one-dimensional (T=0) to being two-dimensional. It will thus assume rational dimensions as its string scale 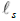varies.

We now proceed to explain why space-time and energy are equivalent by analyzing black hole entropy and using a result in Riemannian Geometry. Such result is the Soul Theorem established by Cheeger and Gromoll. A black hole’s surface area, and the black hole in general, expands in size as matter falls in it. It is also known that space-time contracts as one approaches the singularity. The fact that black holes contain expanding and contracting regions implies that between them must exist a stationary and thus flat region. That is, one cannot pass abruptly from an expanding region to a contracting one. We now discuss black holes’ connection to the Soul Theorem. Such result states that if a manifold’s curvature is null in some regions and positive in the rest, then such manifold M contains a submanifold called a soul, which contains the whole topology of M [1]. In mathematical terminology, the soul is diffeomorphic to M.

Such result applies to black holes since they have positive curvature in their expanding and contracting regions but null curvature between them. We therefore observe that black holes contain souls. Yet where is such soul located? Knowing that a black hole’s information is stored in its surface area [2], and knowing that souls contain their manifold’s whole topology (and thus information about the manifold’s structure), we are led to conclude that a black hole’s soul is equivalent to its surface area. Yet why is the soul equal to the whole surface area and not a portion of it instead? A submanifold is a manifold in its own right and cannot be equal to an arbitrarily local region of its containing manifold. Since black holes’ souls and surface areas are equal, they must contain the same type of information. This means that the information that black holes store is about their topological properties. This is information about space-time’s structure, but what about information regarding the particles that fell into the black hole? Since the soul (and thus surface area) contains only information about space-time’s topology, we are led to conclude that space-time is equivalent to energy and therefore has a fractal structure. A direct consequence of this equivalence is that singularities do not exist. Since strings are the smallest units of energy and cannot have an arbitrarily small size, then space-time itself cannot reach an infinitesimal size like singularities do.

Experimental

Mathematical formulation

Let us begin to construct the equation describing such results by squaring the string’s tension,

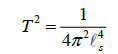
and rearranging it such that,

We now subtract both sides by 4πg,where g is a surface’s genus, obtaining the Gauss-Bonnet Theorem;

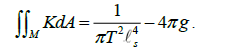
The following step consists on considering the cosmological constant in a De Sitter Space,

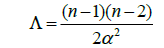
for n De Sitter Space’s dimension and α a constant with units of length. Since we reached the conclusion that space-time has a fractal structure, we now treat n as the Hausdorff dimension, which is given by the power law p = qⁿ for p and q parameters. The following step is to consider the genus-degree formula:

g=(d-1)(d-2)/2

for d the degree of a plane curve. It must be remarked that it is known that the genus of the curve, called the arithmetic genus, is in agreement with the usual topological genus of a surface. Since both the Hausdorff dimension and the curve’s degree are exponents, we can rewrite the cosmological constant as:

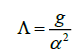
obtaining us the following,

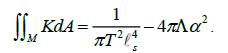
We now multiply both sides by π and set L=2πα, yielding the equation’s final form,

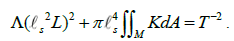
Results, Discussion and Conclusion

We finish this paper by proving the above assertions and explaining some predictions of the equation. The space-time and energy equivalence is already established by the argument used above, namely the application of the Soul Theorem to black holes. This means that we are able to set 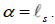Since strings are the smallest unit of energy and thus of space-time, and α has length unit, one can set them equal. This in turn makes the right side of our equation nontrivial by assigning a given string scale to both sides. Also, the string and 2-brane equivalence is proven since for a given string tension T, one will always have a surface M (2-brane) in the left side of the equation.

We now finish by describing a prediction of such equation and explaining how the results obtained here settle some open problems in physics. The prediction is that the Universe is a three-dimensional torus. The space-time and energy equivalence implies that space-time cannot be infinite. Such equality also implies that the Universe’s curvature is zero. That is, since they are the same entity, inhomogeneity cannot rise and the density parameter must equal 1, yielding a flat Universe. By plugging in n=3 into the equation, one obtains g=1, which is a torus.

The first problem regards why the Universe had an extremely low entropy in the past, resulting in the Second Law of Thermodynamics’ existence. The paradox lies in that entropy was very low with respect to gravitational degrees of freedom at the Big Bang. If we imagine the Universe going back in time, it would start getting smaller and denser, up to the point where at the Big Bang it would have extremely high curvature with many black holes. Yet such conclusion contradicts experience for had the Big Bang been disordered, no Second Law of Thermodynamics would exist. The problem is therefore how the Universe managed to be extremely small and dense, and yet not have gravity activated. This is answered by the conclusion that the Universe is a three-dimensional torus. That is, as one goes back in time, the torus would naturally get smaller and denser as it reaches the Big Bang. But since it is a torus, when it finally reaches the Big Bang its curvature as a whole would still be zero.

Now, the last problem is that of high temperature superconductivity. As the temperature of the material drops below its critical temperature, it loses electric resistance and turns into a superconductor. The strings in it have extremely low energies and form a condensate. Such low energy means that their string scales are small while their tensions are very high. The strings therefore turn into 2-branes, and since they are all very close and 2-branes are sticky, they form what are called 2-brane stacks. They will therefore form composite 2-branes with two layers and will remain together even though the temperature increases, since they are sticky and now behave as if they were one object. In conclusion, to compute the equation above, one begins with the string scale as input, proceeds to define a space-time dimension, and thus obtains the genus of a 2-brane in n-dimensional space-time. It must be remarked that with the string scale and space-time dimension one can also compute the vacuum Einstein Equation. To finish, one finds the cosmological constant and solves the Gauss-Bonnet Theorem [3-6].

References

1. Cheeger, Gromoll, Detlef. On the structure of complete manifolds of nonnegative curvature. Annals of Mathematics Second Series. 1972;96:413-43.
2. Hawking SW. Particle creation by black holes. Communications in Mathematical Physics. 1975; 43:199-20.
3. Ellis GFR, Hawking SW. The large scale structure of space-time. Cambridge University Press. 1973;131-13.
4. Spradlin M, Strominger A, Volovich A. Les Houches Lectures on De Sitter Space. 2001.
5. Penrose, Roger. Cycles of Time. New York; Vintage Books. 2010.
6. Laughlin, Robert. A Different Universe. New York; Basic Books. 2005.