Original Article
, Volume: 5( 1)Moon, Super-Moon, Planets of the Solar System and Star Vega: Brightness and Size
- *Correspondence:
- Agrawal DC, Department of Farm Engineering, Institute of Agricultural Sciences, Banaras Hindu University, Varanasi 221005, India, Tel: 0542 236 7311; E-mail: Dca_bhu@yahoo.com
Received: December 12, 2016; Accepted: December 22, 2016; Published: January 31, 2017
Citation: Agrawal DC. Moon, Super-Moon, Planets of the Solar System and Star Vega: Brightness and Size. J Phys Astron. 2017;5(1):104.
Abstract
The Moon, moonlight and phases of the Moon and its relatively simple recurring cycle have been of interest since time immemorial to human beings, navigators, astronomers and astrologers. The fact that the Moon’s orbit is close to the plane of the ecliptic and not to Earth's equatorial plane leads to new Moon to full Moon and solar and lunar eclipses also. During the phase of the full Moon, the luminous flux and its apparent size will depend on its distance from the Earth; when the full Moon is at farthest point called lunar apogee, it will be smallest full moon or micro full moon and whilst it is closest to us termed as lunar perigee will appear macro full moon-better known as super-moon, a term coined by astrologer Richard Nolle in 1979. The expressions for the lunar luminous fluxes on the Earth for the extreme positions lunar apogee and lunar perigee are derived for the first time from the students’ point of view. Furthermore, estimates for apparent magnitudes and apparent sizes of full moons corresponding to these positions are also examined. It is shown that full perigee Moon is about 29% brighter and 14% bigger than the full apogee Moon consistent with numbers available in literature. This paper will motivate the students to apply the techniques learnt here to the case of planets which are revolving around the Sun in their respective elliptical orbits having equivalent extreme positions aphelion and perihelion. In addition, students can also assess apparent magnitude of the reference star Vega.
Keywords
Apparent magnitude; Apparent size; Luminous flux; Micro Moon; Planets; Star vega; Super-Moon; Theoretical estimate
Introduction
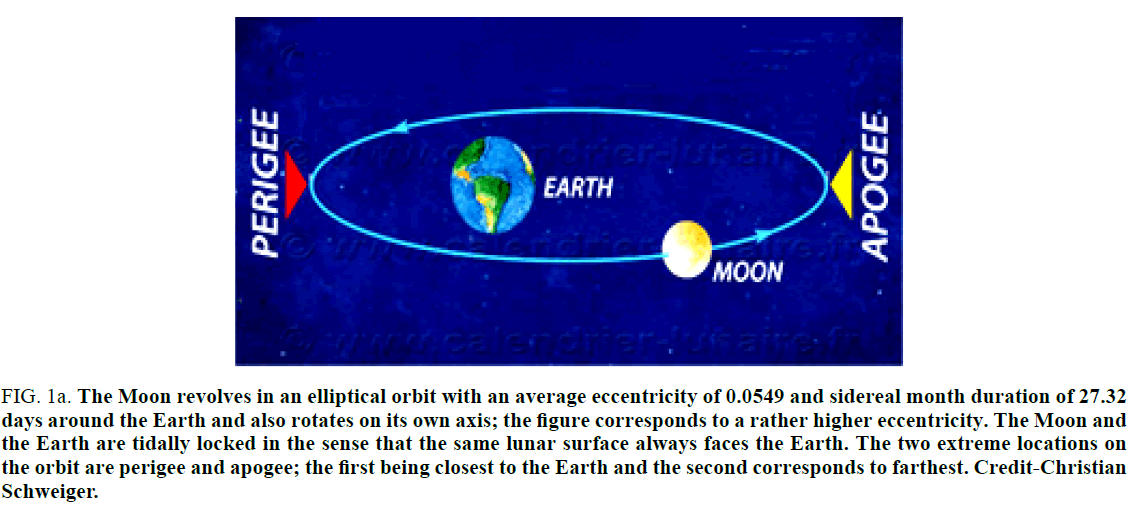
Plato had once said, “Astronomy compels the soul to look upwards and leads us from this world to another”. The Moon is a familiar sight to all of us irrespective of our location on the Earth. From the time humans, have walked the Earth, they have observed with wonder the Moon, moonlight, phases of Moon, full Moon and solar and lunar eclipses. And were anxious to know what really causes the appearance of the Moon to change so drastically? The answer has to do with not just the position of the Moon but the Sun and the Earth as well. The Sun is center of our solar system and the Earth is revolving in an elliptical orbit with eccentricity of 0.0167 around the Sun as astronomical year goes by and rotating on its own axis. At the same time, Moon is also revolving in an elliptical orbit with an average eccentricity of 0.0549, sidereal month duration of 27.32 days around the Earth and rotating on its own axis (Figure 1a and 1b). Changes in the positions of the Moon, Earth and Sun cause various phases of the Moon, solar and lunar eclipses and tides in the oceans. The most early calendars were also based on lunar phases but even nowadays they are used for folkloristic (e.g. astrology) or religious (e.g. the Islamic or Hindu calendars) recurrences.
Figure 1a. The Moon revolves in an elliptical orbit with an average eccentricity of 0.0549 and sidereal month duration of 27.32 days around the Earth and also rotates on its own axis; the figure corresponds to a rather higher eccentricity. The Moon and the Earth are tidally locked in the sense that the same lunar surface always faces the Earth. The two extreme locations on the orbit are perigee and apogee; the first being closest to the Earth and the second corresponds to farthest. Credit-Christian Schweiger.
Figure 1b. The diagram showing the Moon orbiting the Earth with actual Earth-Moon distance to scale. Credit-Brian Koberlein.
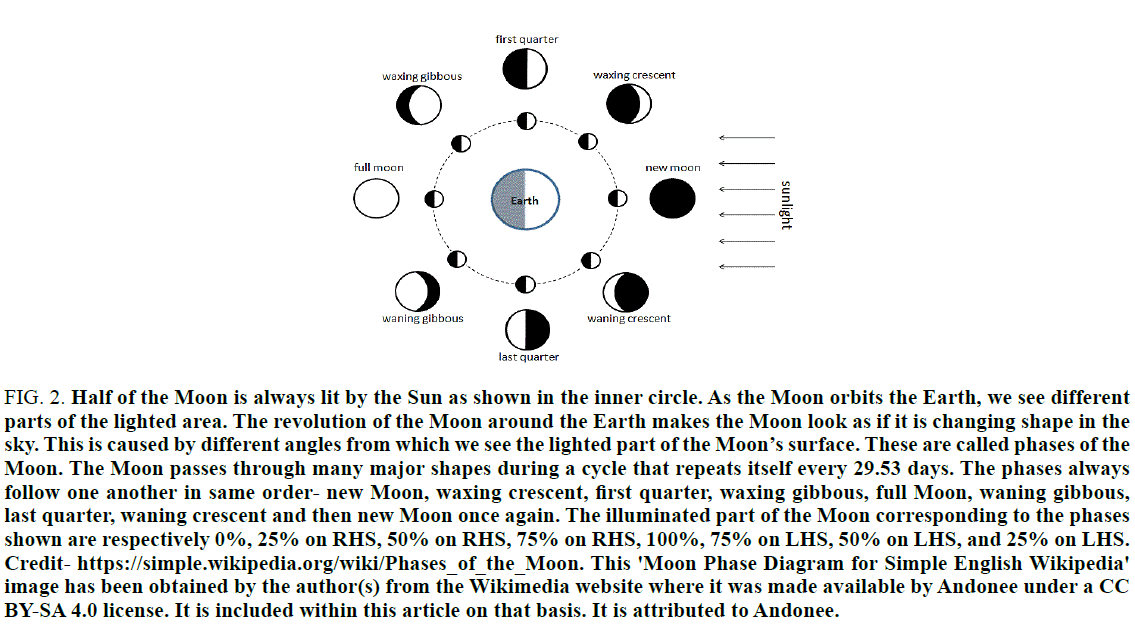
Half of the Moon is always lit by the Sun, although, over time, it’s possible to see as much as 59% of the moon’s surface, due to a slight north-south rocking and east-west wobbling of the Moon known as lunar libration [1,2]. As the Moon orbits the Earth, we see different parts of the lighted area. The revolution of the Moon around the Earth makes the Moon look as if it is changing shape in the sky. This is caused by different angles from which we see the lighted part of the moon’s surface. These are called phases of the Moon. The Moon passes through many major shapes during a cycle that repeats itself every 29.53 days. The phases always follow one another in same order- new moon, waxing crescent, first quarter, waxing gibbous, full moon, waning gibbous, last quarter, waning crescent and then new moon once again (figure 2). The illuminated part of the Moon corresponding to these phases are respectively 0%, 25% on RHS, 50% on RHS, 75% on RHS, 100%, 75% on LHS, 50% on LHS, and 25% on LHS. The phase corresponding to full Moon could be possible because the plane of Moon revolution is inclined at an angle of 5.145 degree with plane of the rotation of the Earth around the Sun-the ecliptic plane; that is why lunar eclipses do not happen more often because during most months the Moon is above or below the Earth.
Figure 2. Half of the Moon is always lit by the Sun as shown in the inner circle. As the Moon orbits the Earth, we see different parts of the lighted area. The revolution of the Moon around the Earth makes the Moon look as if it is changing shape in the sky. This is caused by different angles from which we see the lighted part of the Moon’s surface. These are called phases of the Moon. The Moon passes through many major shapes during a cycle that repeats itself every 29.53 days. The phases always follow one another in same order- new Moon, waxing crescent, first quarter, waxing gibbous, full Moon, waning gibbous, last quarter, waning crescent and then new Moon once again. The illuminated part of the Moon corresponding to the phases shown are respectively 0%, 25% on RHS, 50% on RHS, 75% on RHS, 100%, 75% on LHS, 50% on LHS, and 25% on LHS. Credit- https://simple.wikipedia.org/wiki/Phases_of_the_Moon. This 'Moon Phase Diagram for Simple English Wikipedia' image has been obtained by the author(s) from the Wikimedia website where it was made available by Andonee under a CC BY-SA 4.0 license. It is included within this article on that basis. It is attributed to Andonee.
The luminous flux reaching the Earth depends on the phase of the Moon as well as the moon’s albedo. In fact, the surface of the Moon is non-Lambertian [3] because it is highly backscattering, meaning that it preferentially reflects incoming light back in the direction of illumination. For this reason, the apparent brightness of the lunar surface increases as the phase angle decreases toward zero. This surge in surface brightness near zero phase angles is called the opposition effect [4] or heiligenschein [5]. Full Moon [6] corresponds to (almost) zero phase angle and at new Moon, the phase angle is 180°. At full moon, the Earth, Moon, and Sun are in approximate alignment but the Moon is on the opposite side of the Earth, so the entire sunlit part of the Moon is facing us. The Moon and the Earth are tidally locked in the sense that the same lunar surface always faces the Earth. The shadowed portion is entirely hidden from the view. The perceived size of the full Moon and its luminous flux will depend on its distance from the Earth; whilst it is at farthest point known as lunar apogee (Figure 1a and 1b) the full moon is smallest- called micro full moon and when it is closest to us termed as lunar perigee we observe macro full moon-better known as super-moon. The word ‘super’ was coined by astrologer Richard Nolle [7] in a 1979 issue of Dell Horoscope describing a full moon at perigee-syzygy, that is, a moon which occurs with the Moon at or near (within 90% of ) its closest approach to Earth in a given orbit. The astronomical term for this event has long been a ‘perigean’ full or new Moon, but that wasn’t as catchy [8]. In fact, the word super-moon is rather popular in press, and the term is decried by scientists because of its astrological origin. The aim of the present paper is to estimate and compare the perceived sizes of these two moons and luminous fluxes from them when observed from the Earth.
Now, it will be worth devoting one paragraph on the question of utility of this paper from the students’ point of view. Analogous to the Moon which shines due to the Sun and revolves in an elliptical orbit around the Earth, the eight planets along with one dwarf planet in the solar system also shine due to the Sun and they revolve around it in their respective elliptical orbits. As the Moon encounters apogee and perigee each planet also pass through corresponding extreme positions aphelion and perihelion. The brightness and apparent size of these planets when observed from the Earth will depend on the positions of both the planet and the Earth in their respective orbits; the students should be able to reproduce the associated numbers for all the eight planets revolving around the Sun along with the Earth from where the observations are made. The necessary background for the same is briefly described in the Appendix I for the benefit of the students. This paper will supplement the students’ expertise in evaluating the surface temperatures of these planets based on the reality that solar energy intercepted by every planet is radiated back through the Stefan-Boltzmann expression. For the sake of completeness, apparent magnitude and apparent size of the reference star Vega are also evaluated in the Appendix II.
Theory
The theory part has been developed in a recent publication [9] where the apparent magnitude of earthshine was calculated and compared [10] with that of new astronomical phenomenon moonshine. The theory part can be recapitulated here so that the students are comfortable with the description to follow The electromagnetic solar radiation follows the Planck’s law [11,12]
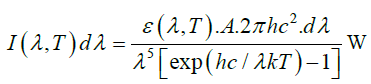 (1)
(1)
for the power emitted between the wavelengths (in meters) λ and λ + dλ from the Sun’s surface having uniform temperature T Kelvin, area A square meter and emissivity ε . Here h and k are Planck’s constant and Boltzmann’s constant, respectively. The above power between the wavelengths 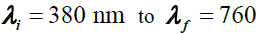 nm is visible to our eyes; however the eye is not equally sensitive [13] to all wavelengths in this region. Rather, its spectral efficiency is optimum at wavelength and becomes vanishingly small outside this interval. This behavior is quantified [9,13,14] by spectral luminous efficiency V (λ ) for photopic vision as a function of λ .
nm is visible to our eyes; however the eye is not equally sensitive [13] to all wavelengths in this region. Rather, its spectral efficiency is optimum at wavelength and becomes vanishingly small outside this interval. This behavior is quantified [9,13,14] by spectral luminous efficiency V (λ ) for photopic vision as a function of λ .
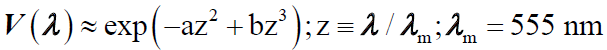 (2)
(2)
a = 88.90, b =112.95
Considering the Sun to be an ideal blackbody (ε =1) the luminous flux emitted from its unit surface area (A =1 m2 ) is obtained by multiplying the power I(λ,T) dλ with 683V (λ) and integrating it over from and integrating it over from λi to λf .
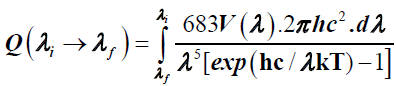 (3)
(3)
The factor 683 occurs because at 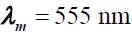 the electromagnetic radiation of one watt provides a luminous flux of 683 lumens. It is worth reminding students here that throughout this paper we will be dealing with luminous flux per unit area which is also called illuminance [15] having SI unit lumen
the electromagnetic radiation of one watt provides a luminous flux of 683 lumens. It is worth reminding students here that throughout this paper we will be dealing with luminous flux per unit area which is also called illuminance [15] having SI unit lumen 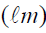 . When the luminous flux
. When the luminous flux 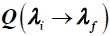 reaches the surface of the Moon it is diluted by the factor [16]α
reaches the surface of the Moon it is diluted by the factor [16]α
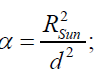 d ≡ yearly mean distance between Moon and Sun. (4)
d ≡ yearly mean distance between Moon and Sun. (4)
giving the value of Solar Luminous Constant On the Moon (SLCOM ) as
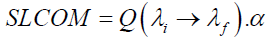 (5)
(5)
The above acronym variable SLCOM represents the amount of solar light arriving at right angle on the moon’s surface covering an area of one square meter. Its unit is lux.
Lunar luminous flux on the Earth
The above flux (5) will be reflected by the layer of charged dust particles originating from the lunar surface [17] of several centimeters thickness having low albedo [18] KMoon and when it arrives on the Earth will be further diluted by the factor
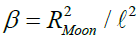 (6)
(6)
Here RMoon is the radius of the Moon and 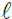 is the distance between the Moon and the Earth. Multiplication of the expression (5) by Moon’s albedo κMoon and the dilution factor β gives the expression for the Lunar Luminous Flux On the Earth (LLFOE) as
is the distance between the Moon and the Earth. Multiplication of the expression (5) by Moon’s albedo κMoon and the dilution factor β gives the expression for the Lunar Luminous Flux On the Earth (LLFOE) as
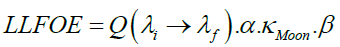 (7)
(7)
Here the acronym variable LLFOE represents the magnitude of lunar light the Earth intercepts in the direction normal to the incidence over an area of one square meter. Its unit is also lux. The condition that the Earth intercepts in the direction normal to the incidence is normally fulfilled during full Moon nights. The value of dilution factor β according to expression (6) is inversely proportional to 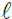 2 where
2 where 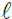 being the distance between the Earth and the Moon; this distance [19,20] varies between approximately 357,000 km (222,000 mi) and 406,000 km (252,000 mi) due to its elliptical orbit around the Earth. The mean distance (
being the distance between the Earth and the Moon; this distance [19,20] varies between approximately 357,000 km (222,000 mi) and 406,000 km (252,000 mi) due to its elliptical orbit around the Earth. The mean distance (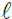 mean ) between Earth and the Moon is 382,000 km. In the event of a full moon occurring while the distance between Earth and Moon
mean ) between Earth and the Moon is 382,000 km. In the event of a full moon occurring while the distance between Earth and Moon 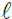 perigee is close to us around 357000 km will be termed as macro moon or super-moon. However, when it is at higher extreme
perigee is close to us around 357000 km will be termed as macro moon or super-moon. However, when it is at higher extreme 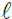 apogee that is around 406, 000 km this is called micro moon (Figure 3). The dilution factor β corresponding to these positions of the Moon will be, respectively
apogee that is around 406, 000 km this is called micro moon (Figure 3). The dilution factor β corresponding to these positions of the Moon will be, respectively
Figure 3. Comparing a perigee full moon (left) with the apogee full moon (right). Credit-Laurent Laveder.
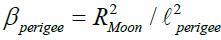 (8a)
(8a)
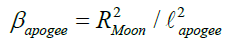 (8b)
(8b)
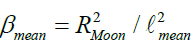 (8c)
(8c)
The expressions for lunar luminous fluxes on the Earth vide (7) will also have different values as follows
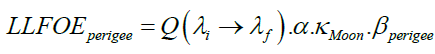 (9a)
(9a)
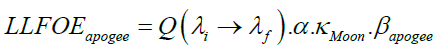 (9b)
(9b)
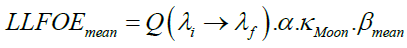 (9c)
(9c)
These are the desired expressions of Lunar Luminous Fluxes on the Earth for the present paper which will be used below to estimate the value of apparent brightness of the Moon corresponding to the positions mentioned above.
Apparent magnitude of micro-moon and super-moon. The human eye is not equally sensitive [9,13,14] to all the wavelengths in the visible region as mentioned above, moreover, its response is also nonlinear [21] to the intensity of light; for example, if one source of light has twice the light as second source then the first source would not appear to eye to be twice bright. The human visual system perceives brightness as the logarithm of the actual light intensity and interprets the image accordingly; for example, a bright light source that is approximately 6 times brighter than another the eye will perceive the brighter light as approximately twice the brightness of the darker. Keeping this point in mind, the magnitude scale has been designed where a difference of 5 magnitudes corresponds to a ratio of brightness 100. This is well known apparent magnitude scale and is represented by a lower case letter m , is a measure of the brightness of an astronomical object as seen by an observer on the Earth and adjusted to the value it would have in the absence of the atmosphere. Generally the visible spectrum is used as the basis for the apparent magnitude to talk about the brightness of stars or any other astronomical object. The brighter the object appears, the lower the value of its magnitude. The apparent magnitude [22] of a body in the visible band having flux F can be defined as,
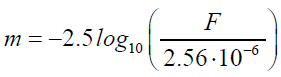 (10)
(10)
Here 2.56⋅10−6 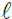 m is the reference luminous flux per unit area in the same bands such that of star Vega having apparent magnitude almost zero; it adjusts the value m it would have in the absence of the atmosphere. The apparent magnitude of the Moon corresponding to perigee and apogee locations will have following expressions
m is the reference luminous flux per unit area in the same bands such that of star Vega having apparent magnitude almost zero; it adjusts the value m it would have in the absence of the atmosphere. The apparent magnitude of the Moon corresponding to perigee and apogee locations will have following expressions
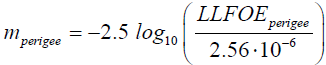 (11a)
(11a)
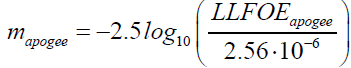 (11b)
(11b)
For the sake of completeness the value of apparent magnitude corresponding to mean position will also be computed from
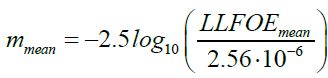 (11c)
(11c)
These are the desired expressions for the apparent magnitudes which will be used in the numerical illustration.
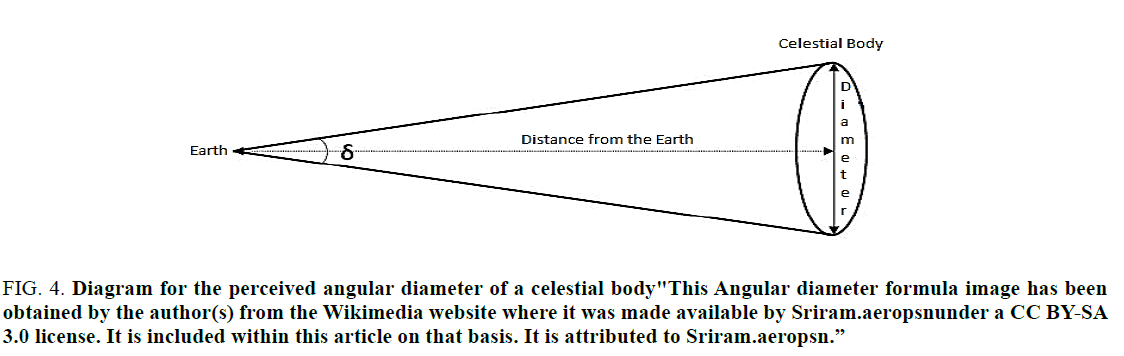
Apparent sizes of micro-moon and super-moon. The apparent size of astronomical object is often presented in terms of its angular diameter as seen from the Earth shown in the Figure 4 and through the formula
Figure 4. Diagram for the perceived angular diameter of a celestial body"This Angular diameter formula image has been obtained by the author(s) from the Wikimedia website where it was made available by Sriram.aeropsnunder a CC BY-SA 3.0 license. It is included within this article on that basis. It is attributed to Sriram.aeropsn.”
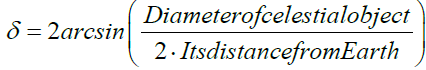 (12a)
(12a)
This expression can be simplified under the small angle approximation resulting in
δ ≅ Diameter of celestial object / Its distance from Earth (12b)
It is common to represent this typically small angular diameter in arc seconds. An arc second is 1/3600th of one degree, while one radian =180 /π degrees and hence one radian = 3600⋅180 /π arcseondswhich is about 206265 arcseconds. Therefore, the perceived angular diameter of the celestial object in arcseconds can be written as
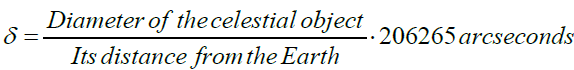 (12c)
(12c)
The full moon perceived by our eyes can be evaluated through the relation
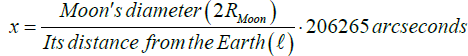 (12d)
(12d)
The expressions for the apparent sizes in two extreme positions will be as follows.
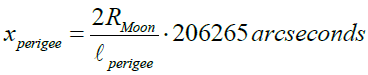 (13a)
(13a)
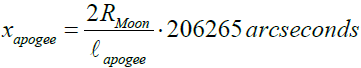 (13b)
(13b)
Once again the perceived size of the Moon corresponding to its mean position (Figure 5) will also be calculated through the relation
Figure 5. Comparison of the super-moon of March 19, 2011 (right) with an average moon of December 20, 2010 (left) as viewed from Earth. "This super-moon comparison image has been obtained by the author(s) from the Wikimedia website where it was made available by Marcoaliaslamaunder a CC BY-SA 3.0 license. It is included within this article on that basis. It is attributed to Marco Langbroek and Carl Zeiss Jen.”
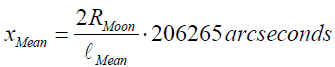 (13c)
(13c)
This will be compared with the apparent size of the Sun HSUN given by
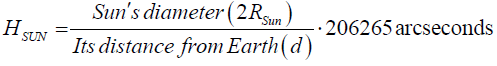 (14)
(14)
to demonstrate that it coincides with the apparent size of the Moon as has been noticed during total solar eclipse. This will be discussed in the next numerical work section.
Numerical work
The integral (3) is evaluated numerically by Simpson’s rule to estimate Q(380→760 nm)in the wavelength region λi = 380nm to λf =760 nm and adopting the values of
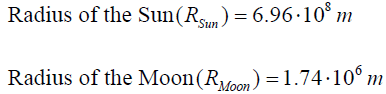
Temperature of Sun’s photosphere(T ) = 5776 K (15)
Distance between Moon and Sun (d)=1.5? 1011 m
Mean distance between Moon and Earth 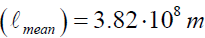
Shortest Distance between Moon and Earth 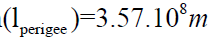
Longest distance between Moon and Earth 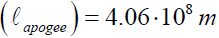
Albedo of the Moon 
as well as the values of fundamental constants Planck’s constant 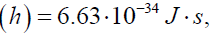 Stefan-Boltzmann Constant
Stefan-Boltzmann Constant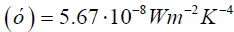 Boltzmann constant
Boltzmann constant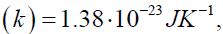 and velocity of light ( c) = 3.0⋅108 mdilution factors
and velocity of light ( c) = 3.0⋅108 mdilution factors 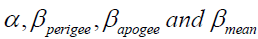 are estimated through expressions (4), (8a), (8b) and (8c), respectively.
are estimated through expressions (4), (8a), (8b) and (8c), respectively.
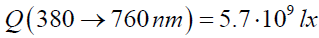 (16)
(16)
α = 2.153⋅10−5 (17a)
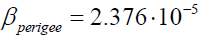 (17b)
(17b)
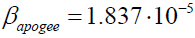 (17c)
(17c)
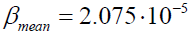 (17d)
(17d)
This will finally give us the desired results which are Solar Luminous Constant on Moon SLCOM and Lunar Luminous Fluxes on the Earth LLFOEperigee , LLFOEapogee and LLFOEmean corresponding to two extreme positions and one mean position full moon through expressions (5), (9a), (9b) and (9c), respectively.
SLCOM =122.7⋅103 lx (18)
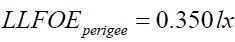 (19a)
(19a)
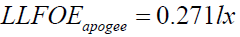 (19b)
(19b)
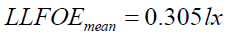 (19c)
(19c)
The luminous flux observed from the Earth during super-moon [23-26] (Figure 6) is approximately 29% larger than that due to micro moon and around 15% more with respect to the mean position full moon (Figure 7).
Figure 6. Pictured is the rise of the perigee full moon over Frankfurt/Main skyline on 19th March 2011. Moonrise was about 15 minutes before full moon and about 80 minutes before the moon reached perigee. Credit-Stephan Heinsius.
Figure 7. Image of an average Moon setting in western sky over the High Desert in California. Credit- https://en.wikipedia.org/ wiki/Moonlicense.
It is worth converting the above fluxes into a better scale for brightness known as apparent magnitude [21,22,27] (10) which is a logarithmic scale as is our eye. The corresponding values , mperigee mapogee and mmean , respectively, are
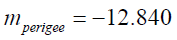 (20a)
(20a)
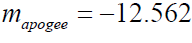 (20b)
(20b)
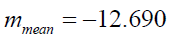 (20c)
(20c)
As far as apparent sizes of the two moons under discussion and the mean position full moon are concerned they can be evaluated via expressions (13a), (13b) and (13c) and the numbers are as follows.
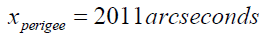 (21a)
(21a)
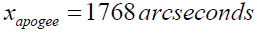 (21b)
(21b)
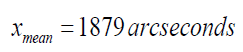 (21c)
(21c)
These numbers show that the apparent size of super-moon [23-26] corresponding to perigee position is around 14% larger than micro moon (Figure 3) and about 7% larger with respect to the mean position full moon (Figure 5). The perceived size of the Sun can be computed from the expression (14). It comes out to be
HSUN =1914 arcseconds (22)
This value is almost equal to the perceived size of full moon at mean position vide (21c) and this is the reason why the Sun is fully covered during total solar eclipse (Figure 8).
Figure 8. The total solar eclipse; this happens while the Moon comes in between the Sun and the Earth and covers the full Sun. This is because the apparent sizes of Sun and Moon are almost equal [cf. (21c) and (22)]. "This Solar eclipse 1999 4 NR image has been obtained by the author(s) from the Wikimedia website where it was made available by Luc Viatour/www.Lucnix. beunder a CC BY-SA 3.0 license. It is included within this article on that basis. It is attributed to Luc Viatour/www.Lucnix. be.”
Conclusions
The Moon is a natural satellite of the Earth and displays a relatively simple recurring cycle from a new Moon to a full Moon. The orbit of Moon being elliptical in nature the two extreme locations on the orbit are perigee and apogee; the first being closest to the Earth and the second corresponds to farthest. The fact that moon’s orbit plane is inclined by 5.145 degree to the plane of rotation of the Earth we observe full moon when the Moon, Earth and the Sun fall on almost in a straight line. The other possibilities are of either total lunar eclipse or total solar eclipse. In both the cases the Sun, Earth and Moon are aligned exactly; whilst during total lunar eclipse the Earth comes between the Sun and the Moon and casts a shadow on the full Moon whereas during total solar eclipse the Moon covers the Sun completely. The aim of the present paper was to find and compare the expressions and values of luminous fluxes reflected by micro and macro full moons as well as their perceived sizes observed from the Earth. The major conclusions of the present work are summarized below.
• The theoretical expressions for the solar luminous constant on the Moon SLCOM [cf. Eq.(5)] which represents the magnitude of solar light arriving at right angle on the moon’s surface covering an area of one square meter and lunar luminous flux on the Earth LLFOE [cf. Eq.(7)] representing the amount of lunar light the Earth intercepts in the direction normal to the incidence over an area of one square meter are derived.
• The value of solar luminous constant over the Moon comes out to be SLCOM =122.7⋅103 lx ; this is comparable with that observed [28] on the Earth.
• The reflected lunar luminous flux intercepted by the Earth corresponding to two extreme positions, perigee and apogee, are 0.350 lx and 0.271 lx, respectively; the perigee full moon is macro moon known as super-moon while apogee one is micro moon. These values suggest that Super-Moon is 29% brighter than micro moon which is consistent with the quoted value of 30% in the literature [23-26].
• A better scale for brightness known as apparent magnitude (10) which is a logarithmic scale as is our eye has been discussed and the corresponding values are 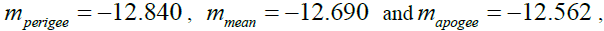 respectively. The respective apparent magnitudes quoted by Schmidt [29] are around −13.2 , −12.7 and −12.4 from the measurements of the moon’s luminance near the full moon performed on January 11th, 2009 at three sites near Dortmund, and south of Heidelberg, all in Germany. Peter Grego [30] has quoted apparent magnitude −12.7 for the full Moon during mean position in the orbit.
respectively. The respective apparent magnitudes quoted by Schmidt [29] are around −13.2 , −12.7 and −12.4 from the measurements of the moon’s luminance near the full moon performed on January 11th, 2009 at three sites near Dortmund, and south of Heidelberg, all in Germany. Peter Grego [30] has quoted apparent magnitude −12.7 for the full Moon during mean position in the orbit.
• The apparent size of the super-moon is shown to be 14% bigger than micro full moon and this also coincides with the reports in the literature [21-26,31].
• The perceived sizes of the Sun and the Moon are almost equal and that is why during total solar eclipse the Sun is fully covered by the new Moon.
Acknowledgement
Certain images in this publication have been obtained by the author(s) from the Wikipedia/Wikimedia website, where they were made available under a Creative Commons license or stated to be in the public domain. Please see individual figure captions in this publication for details. Any reuse rights should be checked and permission should be sought if necessary from Wikipedia/Wikimedia and/or the copyright owner (as appropriate) before using or forwarding the image(s).”
References
- Heiken GH, Vaniman DT, French BM. Lunar sourcebook a user’s guide to the moon. Newyork; 1991;58.
- McClure B. How much of the moon can we see from Earth? 2016.
- A hypothetical surface that reflects incident light uniformly into all directions is said to be Lambertian; 1: 559 p.
- Gehrels T, Coffeen T, Owings D, et al. Wavelength dependence of polarization III. The lunar surface. 1964;69:826-52.
- Wildey RL, Pohn HA. The normal albedo of the Apollo 11 landing site and intrinsic dispersion on the lunar heiligenschein. Astrophys J. 1969;158:129-30.
- Heiken GH, Vaniman DT, French BM. Lunar sourcebook a user’s guide to the moon. 1991;558.
- Nolle R, The astrologer runs the website. 2016.
- Temming M. The not very supermoon. 2016.
- Agrawal DC. Apparent magnitude of earthshine: a simple calculation. Eur J Phys. 2016;37:035601.
- Agrawal DC. Earthshine and moonshine are equivalent astronomical phenomena: addendum to apparent magnitude of earthshine: A simple calculation. Eur J Phys. 2016;37:049041.
- Halliday D, Resnick R. Fundamentals of physics. 1988;844:5.
- Ganiel U, Kedem O. Solar energy-how much do we receive?. Phys Teach. 1983;21:573-5.
- Kaufman JE, Christensen JF. Illuminating engineering society of North America. 1985;35.
- Agrawal DC, Leff HS, Menon VJ, et al. Efficiency and efficacy of incandescent lamps. Am J Phys. 1996;64:649-54.
- Schlyter P. stjarnhimlen.se [internet]. Radiometry and photometry in astronomy [cited 2017 Jan 25]. Available from: http://stjarnhimlen.se/comp/radfaq.html
- Alexis de Vos. Endoreversible thermodynamics of solar energy conversion. 1992;18.
- Popel SI, Kopnin SI, Golub AP, et al. Dusty plasma at the surface of the Moon. Solar Sys Res. 2013;(6):419-29.
- nssdc.gsfc.nasa.gov [internet]. Moon Fact Sheet [cited on 2017, Jan 24]. Available from: http://nssdc.gsfc.nasa.gov/planetary/factsheet/moonfact.html
- Rao J and SPACE.com; Scientific American [internet]. Supermoon to rise in weekend sky [cited on Jan 25, 2017]. Available from: https://www.scientificamerican.com/article/supermoon-to-rise/
- anl.gov. [internet]. Developing the Next Generation of Scientists & Engineers [cited Jan 25, 2017]. Available from: http://www.newton.dep.anl.gov/askasci/phy99/phy99371.htm
- Ross HE, Murray DJ. Ed. and Transl. E.H.Weber on the tactile senses. Taylor & Francis, Erlbaum, 1996.
- Organ P. Teacher Resource Bank: GCE Physics A Astrophysics. 2009;22
- Matson J. Tonight’s full moon biggest. brightest of 2008. Scientific Am. December 12, 2008
- Oransky I. Tonight’s moon will rival last month’s massive bright perigee. Scientific Am. January 10, 2009
- Keimig L. Night Photography and Light Painting: Finding Your Way in the Dark (CRC Press, Boka Raton, Florida 2015) Chapter 6.
- science.nasa.gov [internet]. Perigee "Super Moon" On May 5-6 [cited on Jan 25, 2017]. Availablefrom: http://science.nasa.gov/science-news/science-at-nasa/2012/02may_supermoon/
- Schulman E, Cox CV. Misconceptions about astronomical magnitudes. Am J Phys. 1997;65:1003-7.
- Darula S, Kittler R, CA, et al. Gueymard reference luminous solar constant and solar luminance for illuminance calculations. Sol Energy. 2005;79:559-65.
- Schmidt E. Luminance and brightness data for the full Moon Near Perigee on January11, 2009.
- Grego P. The Moon and how to observe it. 2006;50.
- Darula S, Kittler R, CA, et al. Gueymard reference luminous solar constant and solar luminance for illuminance calculations. Sol Energy. 2005;79:44.
- http://nssdc.gsfc.nasa.gov [internet]. Mercury Fact Sheet [cited on Jan 25, 2017]. Available from: http://nssdc.gsfc.nasa.gov/planetary/factsheet/mercuryfact.html
- http://nssdc.gsfc.nasa.gov [internet]. Venus Fact Sheet [cited on Jan 25, 2017]. Available from: http://nssdc.gsfc.nasa.gov/planetary/factsheet/venusfact.html
- http://nssdc.gsfc.nasa.gov [internet]. Earth Fact Sheet [cited on Jan 25, 2017]. http://nssdc.gsfc.nasa.gov/planetary/factsheet/earthfact.html
- http://nssdc.gsfc.nasa.gov [internet]. Mars Fact Sheet [cited on Jan 25, 2017]. http://nssdc.gsfc.nasa.gov/planetary/factsheet/marsfact.html
- http://nssdc.gsfc.nasa.gov [internet]. Jupiter Fact Sheet [cited on Jan 25, 2017]. http://nssdc.gsfc.nasa.gov/planetary/factsheet/jupiterfact.html
- http://nssdc.gsfc.nasa.gov [internet]. Saturn Fact Sheet [cited on Jan 25, 2017]. http://nssdc.gsfc.nasa.gov/planetary/factsheet/saturnfact.html
- http://nssdc.gsfc.nasa.gov [internet]. Uranus Fact Sheet [cited on Jan 25, 2017]. http://nssdc.gsfc.nasa.gov/planetary/factsheet/uranusfact.html
- http://nssdc.gsfc.nasa.gov [internet]. Neptune Fact Sheet [cited on Jan 25, 2017]. http://nssdc.gsfc.nasa.gov/planetary/factsheet/neptunefact.html
- http://nssdc.gsfc.nasa.gov [internet]. Pluto Fact Sheet [cited on Jan 25, 2017]. http://nssdc.gsfc.nasa.gov/planetary/factsheet/plutofact.html
- https://en.wikipedia.org/wiki/Vega
- Solarsystemquick.com [internet]. Vega Star [cited on Jan 25, 2017]. Available from: http://www.solarsystemquick.com/universe/vega-star.htm
- Bohlin RC, Gilliland RL. Hubble space telescope absolute spectrophotometry of Vega from the far-ultraviolet to the infrared. Astronom J. 2004;6:3508-15.
- Samus NN, Durlevich OV, et al. VizieR online data catalog: General catalogue of variable stars. Vizie R On-line Data Catalo. 2009;1:02025.
Appendix-I
Planets of the solar system: brightness and size
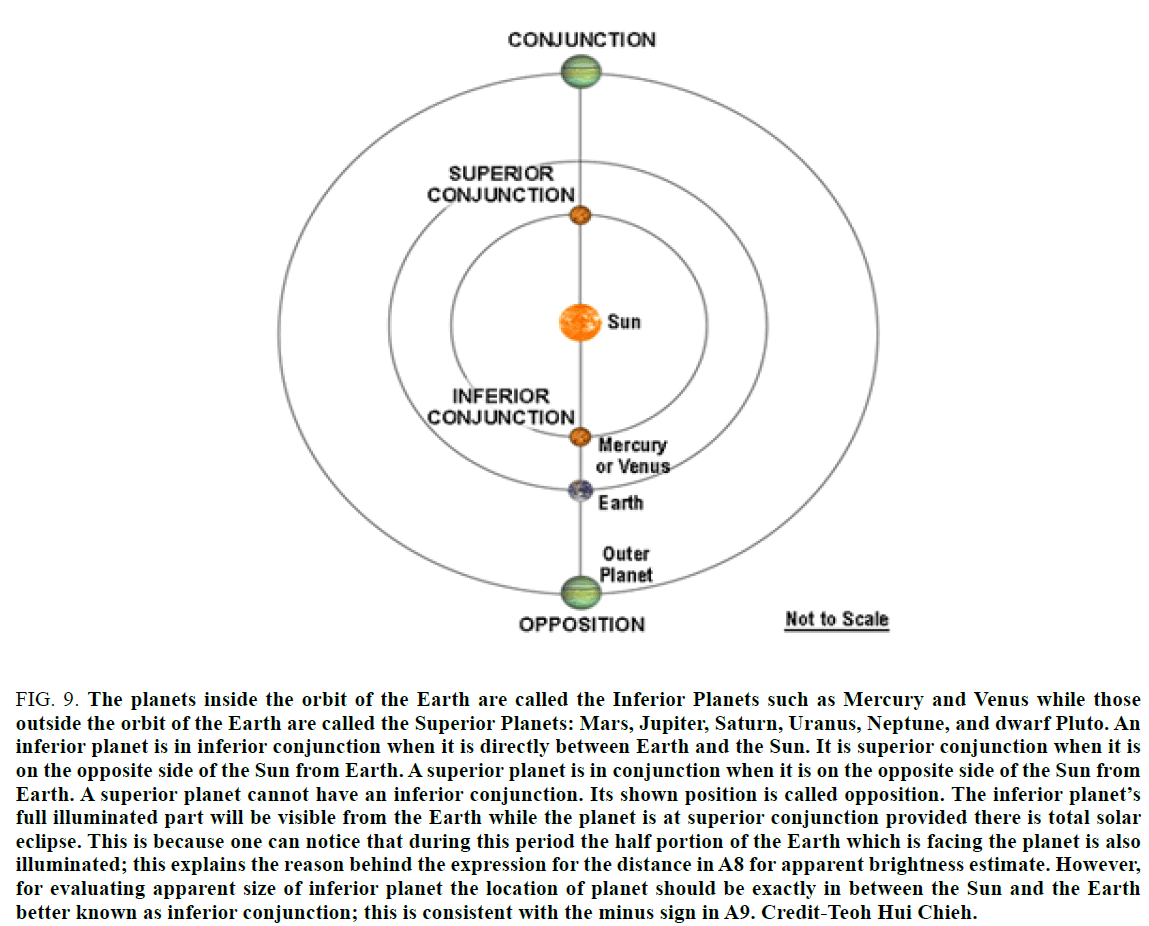
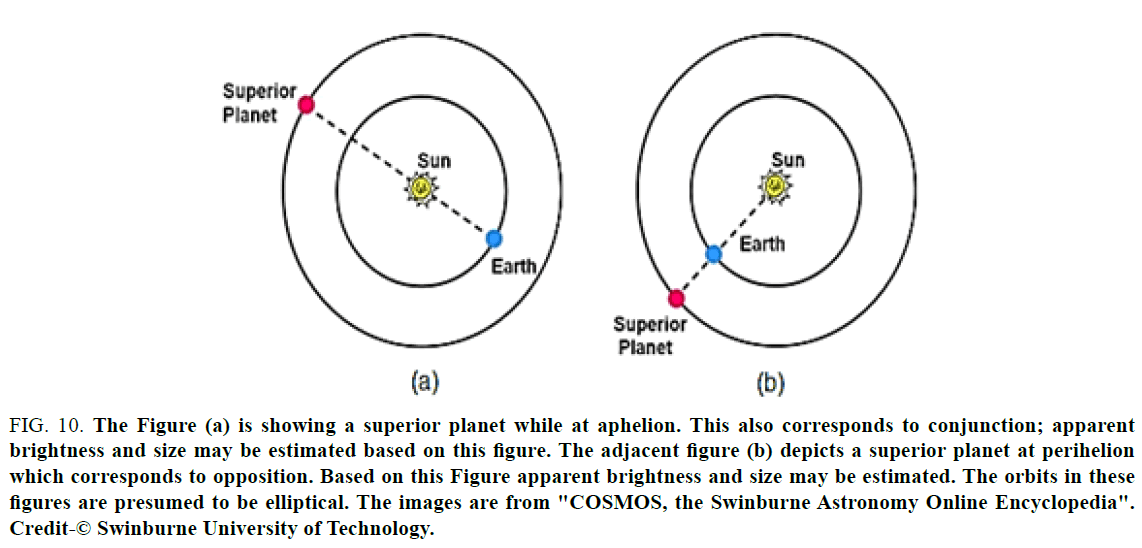
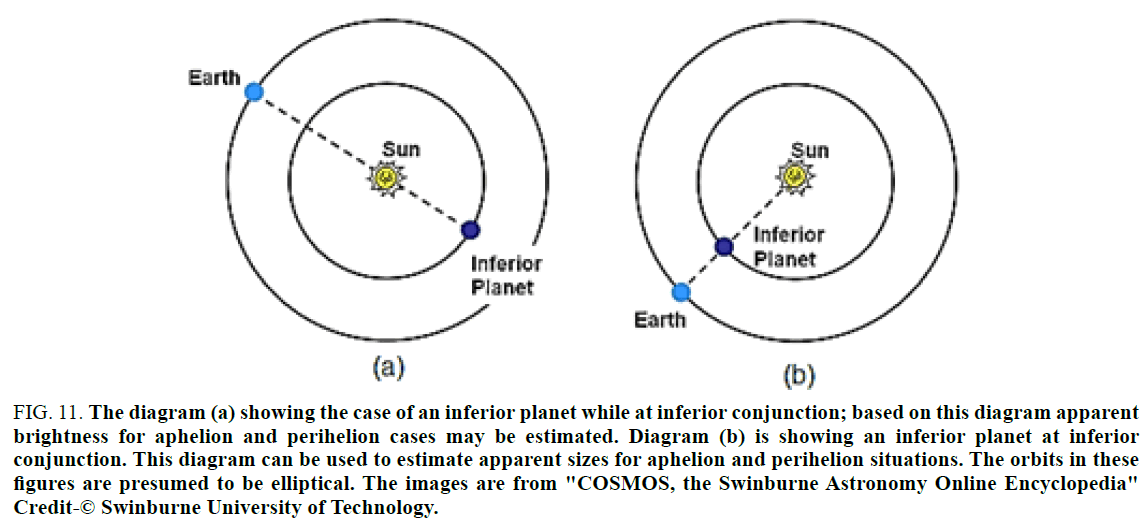
The solar system consists of the Sun, the eight planets, one dwarf planet and their natural satellites. A planet is a celestial body that revolves around the central Sun whereas a natural satellite is also a celestial body but orbits around any solar planet; both the planets and satellites do not shine by their own light. Eight major planets of our solar system are Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune. Pluto, which until recently was considered to be the farthest planet, is now classified as a dwarf planet. Every planet revolves in the same direction which is counter clockwise whilst looking down from above the Sun’s North Pole. The planets inside the orbit of the Earth (Figure 9) are called the Inferior Planets such as Mercury and Venus while those outside the orbit of the Earth are called Superior Planets: Mars, Jupiter, Saturn, Uranus, Neptune, and dwarf Pluto. An inferior planet is in inferior conjunction when it is directly between Earth and the Sun. It is superior conjunction when it is on the opposite side of the Sun from Earth. A superior planet is in conjunction when it is on the opposite side of the Sun from Earth. A superior planet cannot have an inferior conjunction since it is outside the Earth’s orbit. But its status opposite to conjunction is rather called opposition. One can measure experimentally or calculate theoretically the apparent brightness of planets at conjunction (Figure10a), superior conjunction (Figure 11a) and opposition (Figure 10b) but not at inferior conjunction (Figure 11b) because in the first three cases they will be visible from the Earth but in the last situation the illuminated portion will not be visible from Earth at inferior conjunction. However, as far as apparent size is concerned it can be measured in all the cases depicted in Figures 10 and 11.Students, of course, can estimate these quantities based on the expressions to be presented in the sequel for mean orbital distances but since this article is supposed to teach planets elliptical orbits vis-à-vis moon’s elliptical orbit they must also read it.
Figure 9. The planets inside the orbit of the Earth are called the Inferior Planets such as Mercury and Venus while those outside the orbit of the Earth are called the Superior Planets: Mars, Jupiter, Saturn, Uranus, Neptune, and dwarf Pluto. An inferior planet is in inferior conjunction when it is directly between Earth and the Sun. It is superior conjunction when it is on the opposite side of the Sun from Earth. A superior planet is in conjunction when it is on the opposite side of the Sun from Earth. A superior planet cannot have an inferior conjunction. Its shown position is called opposition. The inferior planet’s full illuminated part will be visible from the Earth while the planet is at superior conjunction provided there is total solar eclipse. This is because one can notice that during this period the half portion of the Earth which is facing the planet is also illuminated; this explains the reason behind the expression for the distance in A8 for apparent brightness estimate. However, for evaluating apparent size of inferior planet the location of planet should be exactly in between the Sun and the Earth better known as inferior conjunction; this is consistent with the minus sign in A9. Credit-Teoh Hui Chieh.
Figure 10. The Figure (a) is showing a superior planet while at aphelion. This also corresponds to conjunction; apparent brightness and size may be estimated based on this figure. The adjacent figure (b) depicts a superior planet at perihelion which corresponds to opposition. Based on this Figure apparent brightness and size may be estimated. The orbits in these figures are presumed to be elliptical. The images are from "COSMOS, the Swinburne Astronomy Online Encyclopedia". Credit-© Swinburne University of Technology.
These planets orbits being elliptical there will be two extreme locations; the point closest to the Sun is known as perihelion (the corresponding point for moon is called perigee) whilst the farthest away location is called aphelion (in case of moon this point is called apogee). If we attach the adjective super with the planets also in analogy with super-moon the super-Mercury or super-Venus will be visible from the Earth when the planet concerned and the Earth both are at perihelion, the Sun being in between the planet and the Earth (Figure 11a) so that the illuminated portion of the planet is facing the Earth, and there is total solar eclipse. The solar eclipse creates the necessary dark background thereby illuminated inferior planet may be observed from the Earth; this is because during super- Mercury or super-Venus conjunction it will be day time on the Earth also and these planets cannot be viewed from the Earth in the day sunlight. However, the super-Mars, super-Jupiter, etc. can be viewed from the Earth when the concerned planet and the Earth are passing through perihelion and are on the same side of the Sun (Figure 10b); this happens so when the dark side of the Earth is facing these shining planets. Similarly, by making use of the adjective micro in analogy with micro-moon, micro-Mercury, micro-Venus, micro-Mars, and so on can be observed from the Earth whilst the concerned planet and the Earth are at aphelion, on opposite sides of the Sun (Figure 10a and 11a), and during total solar eclipse short period. The elliptical plane of revolution of each planet has relatively small inclination with plane of the rotation of the Earth around the Sun-the ecliptic plane; that is why full illumination of a planet could be sighted from the Earth since the chance of the planet being above or below the ecliptic plane is quite large during the situations under discussion. The students having understood the points discussed so far can proceed to write the corresponding expressions for the planets as follows:
Figure 10. The diagram (a) showing the case of an inferior planet while at inferior conjunction; based on this diagram apparent brightness for aphelion and perihelion cases may be estimated. Diagram (b) is showing an inferior planet at inferior conjunction. This diagram can be used to estimate apparent sizes for aphelion and perihelion situations. The orbits in these figures are presumed to be elliptical. The images are from "COSMOS, the Swinburne Astronomy Online Encyclopedia" Credit-© Swinburne University of Technology.
1. The super-Mercury or super-Venus case
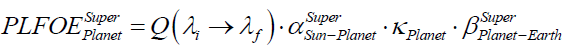 (A1)
(A1)
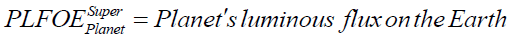 (A2)
(A2)
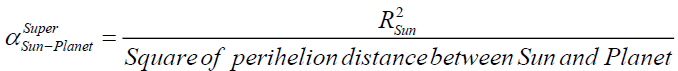 (A3)
(A3)
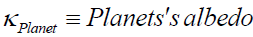 (A4)
(A4)
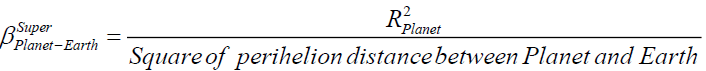 (A5)
(A5)
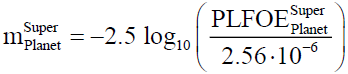 (A6)
(A6)
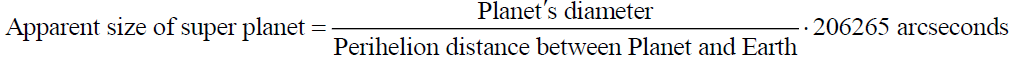 (A7)
(A7)
Perihelion distance between Planet and Earth (Apparent brightness) = Perihelion distance between Sun and Planet + Perihelion distance between Sun and Earth (A8)
Perihelion distance between Planet and Earth (Apparent size) = Perihelion distance between Sun and Planet - Perihelion distance between Sun and Earth (A9)
Students may be somewhat puzzled to see two expressions for the distances between the inferior planet and Earth when they are at perihelion. For apparent brightness the planet must be illuminated by the Sun and this is possible while the planet arrives at superior conjunction on other side of the Sun so that its illuminated half portion may be seen from the Earth (Figure 11a) during total solar eclipse (eclipse has not been shown); this justifies the addition operation in (A8). However, for the apparent size of the planet both the planet and the Earth should be on the same side at perihelion inferior-conjunction (Figure 11b); this explains the occurrence of negative sign. It is worth reminding here that in both events it is presumed that the planet, the Earth and the Sun are aligned as shown in the figures.
2. The Super case for remaining planets- Mars, Jupiter, Saturn, Uranus, Neptune and dwarf Pluto (Figure 10b). There will be only one change as follows:
Perihelion distance between Planet and Earth = Perihelion distance between Sun and Planet - Perihelion distance between Sun and Earth (A10)
3. The micro case for all the eight planets and dwarf planet (Figure 10a and 11a).
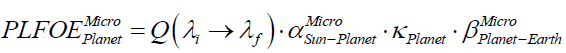 (A11)
(A11)
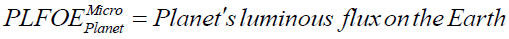 (A12)
(A12)
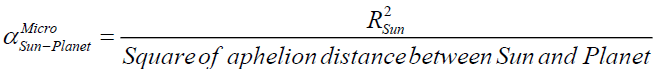 (A13)
(A13)
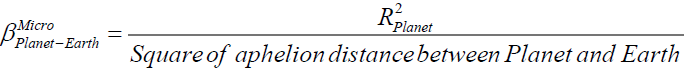 (A14)
(A14)
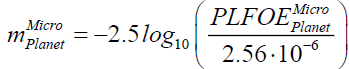 (A15)
(A15)
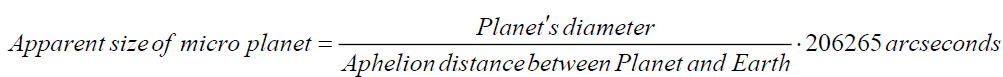 (A16)
(A16)
Aphelion distance between Planet and Earth = Aphelion distance between Sunand Planet + Apheliondistance between Sunand Earth (A17)
In case of micro planets in analogy with micro moon both for brightness and size the concerned planet and Earth should be on the opposite sides of the Sun at aphelion (Figure 10a and 11a) as evident with the positive sign in (A17). Employing characteristic data[32-40] of planets from Table I in the above mentioned expressions apparent magnitudes and apparent sizes of the eight planets of the solar system are estimated (Table II). The major findings are listed below.
| Planet and its mean radius in (106) meters | Perihelion distance from the sun in (109) meters | Aphelion Distance from the Sun in (109) meters | Visual albedo | Super apparent magnitude | Apparent super diameter in Arcseconds | Apparent micro diameter in Arcseconds |
|---|---|---|---|---|---|---|
| Mercury 2.44 |
46 | 69.8 | 0.142 | -1.9 | 13 | 4.5 |
| Venus 6.052 |
107.5 | 108.9 | 0.65 | -4.6 | 66 | 9.7 |
| Earth 6.371 |
147 | 152.1 | 0.367 | -3.86 | - | - |
| Mars 33.895 |
206.6 | 149.2 | 0.17 | -2.91 | 25.1 | 3.5 |
| Jupiter 69.911 |
740.5 | 816.6 | 0.52 | -2.94 | 50.1 | 29.8 |
| Saturn 58.232 |
1352.6 | 1514.5 | 0.47 | 0.43 | 20.1 | 14.5 |
| Uranus 25.362 |
2741.3 | 3003.6 | 0.51 | 5.32 | 4.1 | 3.3 |
| Neptune 24.622 | 4444.5 | 4545.7 | 0.41 | 7.78 | 2.4 | 2.2 |
| dwarf Pluto 1.187 | 4436.8 | 7375.9 | 0.6 | 13.65 | 0.11 | 0.06 |
Table 1. Astronomical data reproduced from NASA fact sheets [32-40] for the nine planets of the solar system
| Planet | Super apparent magnitude | Micro Apparent magnitude | Super apparent size | Micro apparent size |
|---|---|---|---|---|
| Mercury | -2.658 | -1.459 | 9.96 | 4.535 |
| Venus | -3.839 | -3.754 | 63.18 | 9.564 |
| Mars | -2.85 | -1.692 | 23.43 | 3.484 |
| Jupiter | -2.88 | -1.604 | 48.59 | 29.77 |
| Saturn | 0.474 | 1.422 | 19.93 | 14.41 |
| Uranus | 7.834 | 6.012 | 4.033 | 3.315 |
| Neptune | 7.834 | 8.077 | 2.364 | 2.162 |
| Dwarf Pluto | 14.0 | 16.32 | 0.114 | 0.065 |
Table 2. Estimate of apparent magnitudes and apparent sizes of the eight planets of the solar system
• The super apparent magnitudes of the entire eight planets match very well with the ones quoted in NASA fact sheets.
• The micro apparent magnitudes are also calculated for eight planets but the corresponding experimental numbers are not available in the literature, therefore, they could not be compared.
• The super apparent and micro apparent sizes of all the eight planets are also reproduced precisely as quoted by NASA.
• It is observed that the brightest planet in our solar system is the Venus.
• It may be inferred from the examination of super and micro apparent magnitudes of the planets Mercury, Mars, and Jupiter that either of the planets may be brighter than the other two depending upon their locations in the sky.
• The Uranus can be only just observed through naked eyes since its apparent magnitude is around six. An astronomical object can be observed through naked eyes up to apparent magnitude of six.
• Both Neptune and dwarf Pluto planets cannot be viewed from the Earth through naked eyes and one has to look through a telescope for observing Neptune and dwarf Pluto.
Appendix-Ii
Vega Star
For the sake of completeness, it will be worth extending the above formulation to the case of reference star Vega (Figure 12) for the benefit of the students. One may write expressions for luminous flux emanating from star Vega (vide 3), dilution factor for the flux arriving on Earth (vide 4), and magnitude of Vega star luminous flux observed from the Earth (vide 5) as follows
Figure 10. Vega is the brightest star in the constellation Lyra, the fifth brightest star in the night sky. It is a relatively close star at only 25 light-years from Earth. Credit- Matt Mercer (c) http://www.astronovice.com/vega/
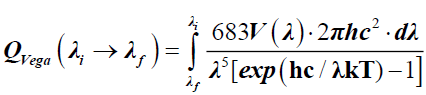 (A18)
(A18)
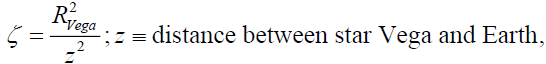 (A19)
(A19)
RVega ≡ Radius of star Vega
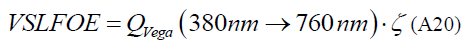
Taking values of the parameters of star Vega [41,42]
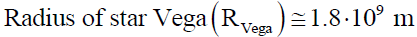 (A21)
(A21)
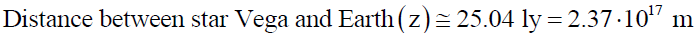 (A22)
(A22)
Temperature of Vega star (T) = 8152-10060 K (A23)
quantities of interest  VSLFOE and corresponding apparent magnitudes were computed for temperature range8152-10060 K ; the former being the polar temperature while the latter is equatorial temperature (Table III). It may be added that Vega is seen from the Earth nearly pole on [41]. Thus the surface visible to us is the one which is enclosed within equatorial perimeter; actually an oblate spheroid. For the sake of simplicity the mean of equatorial
VSLFOE and corresponding apparent magnitudes were computed for temperature range8152-10060 K ; the former being the polar temperature while the latter is equatorial temperature (Table III). It may be added that Vega is seen from the Earth nearly pole on [41]. Thus the surface visible to us is the one which is enclosed within equatorial perimeter; actually an oblate spheroid. For the sake of simplicity the mean of equatorial  radii of Vega has been adopted. The evaluated apparent magnitudes mVega have the range +0.76 to +0.06 which is comparable with magnitude +0.026 quoted by Bohlin and Gilliland [43], and the range -0.02-0.07 reported by Samus and Durlevich [44]. The apparent size of Vega star will be 0.00313 arcsecond.
radii of Vega has been adopted. The evaluated apparent magnitudes mVega have the range +0.76 to +0.06 which is comparable with magnitude +0.026 quoted by Bohlin and Gilliland [43], and the range -0.02-0.07 reported by Samus and Durlevich [44]. The apparent size of Vega star will be 0.00313 arcsecond.
| Temperature of Vega Star | 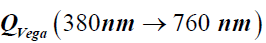 |
VSLFOE | mvega |
|---|---|---|---|
| 8152 K | 2.205?1010 | 1.273?10-6 | 0.76 |
| 10060 K | 4.196?1010 | 2.42?10-6 | 0.06 |
Table 3. Estimate of luminous flux emanating from star 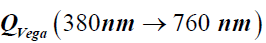 (vide A18), magnitude of Vega star luminous flux observed from the Earth mvega (vide A20), apparent magnitude mvega (vide 10) for dilution factor for the flux arriving on Earth (vide A19) æ= 5.77⋅10−17.
(vide A18), magnitude of Vega star luminous flux observed from the Earth mvega (vide A20), apparent magnitude mvega (vide 10) for dilution factor for the flux arriving on Earth (vide A19) æ= 5.77⋅10−17.