Original Article

, Volume: 16( 1)

• View PDF
• Download PDF

Mixed Convective Flow of a Non-Newtonian Fluid with Permeable Walls by Considering the Influence of Acceleration Due to Gravity

*Correspondence:

Kalpana S, Research Scholar, Department of Mathematics, Krishna University, Machilipatnam, India, Tel: 08672225963; E-mail: kalpana.sanampudi@gmail.com

Abstract

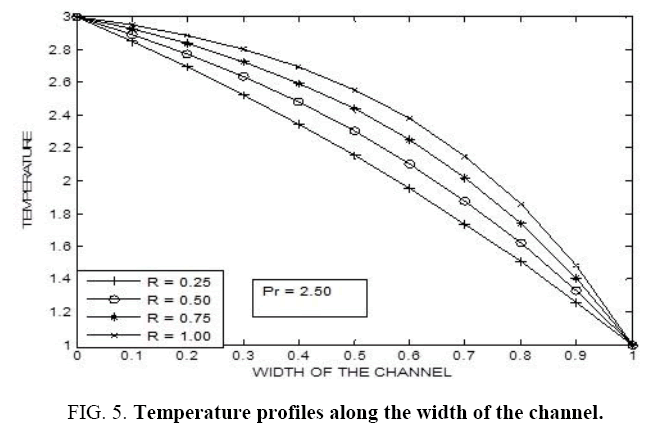
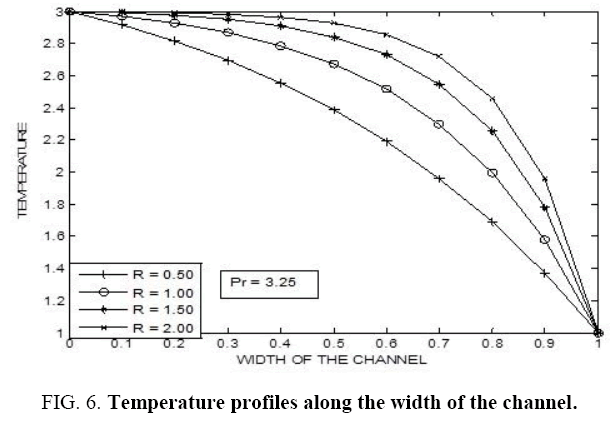
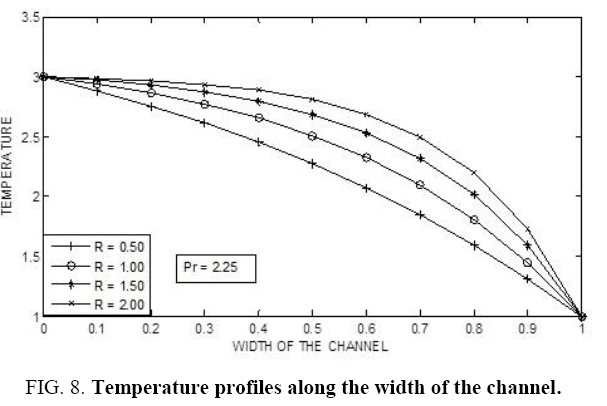
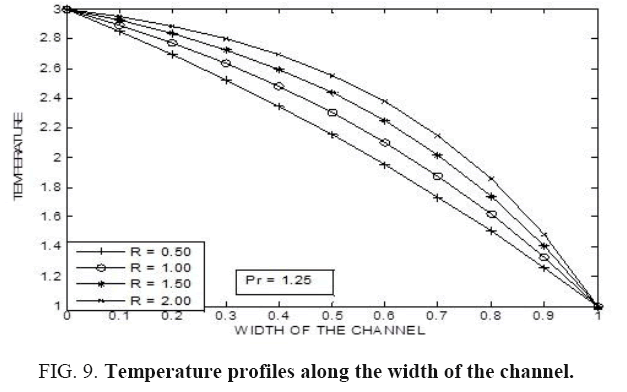
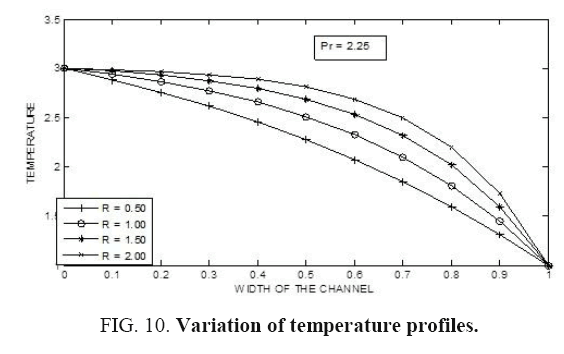
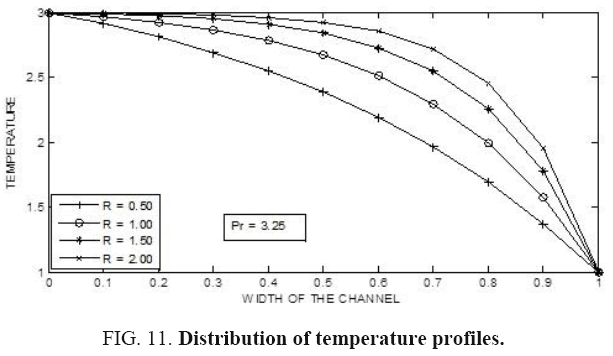
In this paper, the situation of Mixed Convective Flow of a Non-Newtonian Fluid with permeable walls by considering the influence of acceleration due to gravity has been examined in detail. It is noticed that, as Prandtl number increases the temperature also increases. Not much of significant change is observed when the radiation parameter (R) is slightly decreased. However, a drastic change is seen when the Prandtl number changes considerably along with the radiation parameter (R). Further, it is noticed that, as the radiation parameter (R) increases the temperature in the fluid also increases. However, not much of significant change is noticed for a small change in the Prandtl number. But, there is a significant change in the profiles for larger values of Prandtl number (Pr). It is seen that, as we move far away from the lower boundary then the temperature is found to be decreasing. Further, it is observed that, as the radiation parameter (R) increases the temperature of the fluid decreases.

Keywords

Newtonian fluid; Reynolds number; Prandtl number; Radiation parameter

Introduction

In recent years, fluid mechanics had made significant progress in many segments of engineering, science and technology sectors. In this paper, an attempt has been made to explain the possibility of supporting thermal transfer in many industrial and technological applications. Experimental situations related to relevant phenomena should be very specific. Engineering systems especially are generally complicated and experimentally confusing. It is characterized by the complex currents where the fluid stream currents often have a sudden change with reference to the geometry. This of course is not uncommon, but it needs to be studied in detail. In recent years, exploration of oil and the extraction of geothermal energy from the deepest part of the earth, evaluation of heat removal capacity from nuclear fuel debris, nuclear reactors, flow of liquids through ion-exchange beds, drug permeation through human skin and glands etc. are some of the wide-ranging applications. Further, due to extensive applications of physics, chemistry and chemical technology had shown considerable interest in theoretical and experimental investigations over the past few decades. In all experiments, where the transfer of liquid from one container to another is involved, the rate at which such transfer takes place and the thin film adhering to the surfaces of the container is to be taken in to account, for the purpose of chemical calculations. Failure to do so leads to experimental error. Therefore, such an analysis is required. Analyzing the skin friction that affects the boundary is responsible for the safety of chemical reactors which is a most important factor. Generally, in the chemical processing industries slurry adheres to the walls of the container and gets consolidated. As a result, the chemical compound within the reactor vessel percolates through the boundaries causing loss of production and then consuming more reaction time. The slurry thus formed inside the reactor vessel often acts as a porous boundary for the next cycle of chemical processing.

The porous medium can be considered as an ordered flow in a disordered geometry. A porous medium may be either an aggregate of large number of particles such as sand or a solid containing more capillaries such as a porous rock. When the fluid percolates through a porous material, because of complexity of microscopic flow in the pores, the actual part of an individual fluid particle cannot be analytically analyzed. However, the process can be defined in terms of equilibrium forces.

Experimental

The resistance force is characterized by Darcy's semi-empirical law set up by Darcy [1]. The simplest model for flow through a porous medium in one dimensional model derived by Darcy [1]. Heat transfer in the porous media has become most prominent due to the exploitation of geothermal energy, nuclear waste disposal, fossil fuel identification, regenerator bed, etc. Using the method of similarity solution, Murthy and Singh [2] studied the effect of lateral mass and thermal penetration in porous media. Later, Cheng and Minkowycz [3] analyzed sustainable free convection of vertical plates on porous dynamics in the form of dissipative inequality (Clausius – Duhem), and generally accepted idea of the specific Helmholtz free power balance must be minimum in the equilibrium state. Subsequently, Dupit and Frochheimer presented empirical evidence,

MacDonald et al. [4] and others presented the balance between speed and pressure variations, breaks down for large enough flow speed (compilation of many experimental results). This was subsequently emphasized by Joseph et al [5] who stressed that Frochheimer’s actions were forced to work in the opposite direction to the velocity vector. In a multi-stream flow, it follows that the momentum equations are at least predictable for each speed component derived by Frochheimer's expanded Darcy equation. The effects of the existence of solid boundary and the presence of initial forces on mass transfer in Porous Media were submitted by Vafai and Tien [6]. Later, Knupp and Lage [7] analyzed the theoretical generalization to the tensor permeability case of emphatically obtained Frochheimer's extended Darcy’s unidirectional flow model. Thereafter, MacDonald et al. [8] presented the balance between speed and pressure contradictions: a large enough flow rate (compilation of many experimental results).

The local volume average method was used to establish the governing equations. The numerical solution of governing equations is used to examine the mass concentration field in a porous media which is close to an impermeable boundary. A transitional mass transfer experiment was conducted to demonstrate boundary and inertial effects on mass transfer, combined with numerical solution. This is possible by estimating the average mass flux through a porous medium. Non-Darcy natural convection over a vertical plate in porous medium has been the subject of interest. Also, the effect of lateral mass and thermal penetration in thermal conduction was studied.

Further, they had discussed the combined effect of heat exchanges and liquid injection on Darcy mixed transfer. Hassain et al [9] studied the effects of heat dissemination and side effects on mixed synthesis problems and established the trend of heat transfer rate from a vertical plate in porous medium and researched in drain and temperature sectors. Later, Kuznetsov [10] examined the effect of transverse thermal dispersion on forced convection in porous media and found favourable conditions for heat transfer with dispersion effects. Mohahammadien and El-Amin [11] studied the dispersion and radiation effects in fluid saturated porous medium and the effects of radiation on the heat transfer rate for both Darcy and non-Darcy Medium. Cheng and Lin [12] in their observation pointed out that the rate of unsteady heat transfer can be accelerated by thermal dispersion. Without taking MHD into consideration Chamka and Quadri [13] examined the heat and mass transfer properties in mixed convective conditions. Wang et al [14] applied in explicit analytical techniques namely homotopy analysis to solve the Non-Darcy natural convection over a horizontal plate with surface mass flux and thermal diffusion and obtained a totally analytic and uniformly valid solution.

Formulation of the problem

We consider the laminar mixed convection flow of a Newtonian fluid through a porous medium in a vertical permeable channel, the space between the plates h being the same. It is expected that the rate of injection at a wall is equal to the suction rate at the other wall. A rectangular coordinate system (x, y) x-axis is parallel to the gravitational acceleration vector , the y-axis is perpendicular to the x-axis. The left wall (i.e., y=0) is maintained at constant temperature T₁ and the right wall (at y=h) is maintained at constant temperature T₂. It is always maintained that T₁>T₂. The flow is assumed to be laminar, steady and is fully developed, i.e., the transverse velocity is zero. Then the equation of continuity drops down to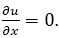

The basic equations of momentum and energy governing such a flow, subject to the Boussinesq approximation, are

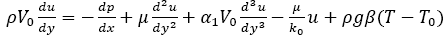(1)

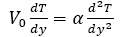(2)

Where p is the pressure, ρ is the density, μ is the dynamic viscosity of the fluid, g is the acceleration due to gravity, β coefficient of thermal expansion, α₁ is the viscoelastic parameter, k₀ is the permeability of the porous medium and V₀ is the transpiration cross flow velocity. Further, here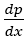 is a constant.

The boundary conditions are given by,

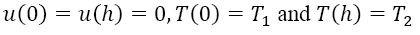(3)

Introducing the following non-dimensional variables:

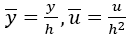and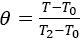 into the equations (1) and (2), we obtain

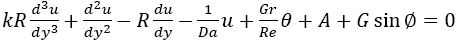(4)

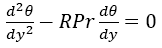(5)

where 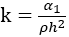is the viscoelastic parameter, 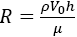is the cross flow Reynolds number, 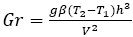is the Grashoff number, 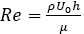is the Reynolds number, 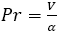is the Prandtl number, 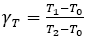is the wall temperature parameter, 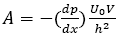is the constant pressure gradient.

The corresponding dimensionless boundary conditions are given by,

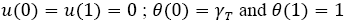(6)

Solution of the problem

We consider the first order perturbation solution of the BVP (1)-(2) for small . The perturbation solution obtained by retaining the terms up to the same order of smallness of k must be quite logical and reasonable. We write,

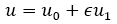(7)

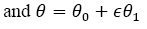(8)

Substituting equations (7) and (8) into equations (4) and (5) and boundary conditions (6) and then equating the like powers of, we obtain,

Zeroth-order system :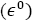

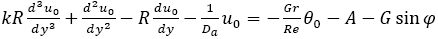
Under the assumption that 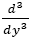is negligible the above equation reduces to

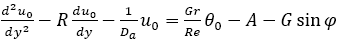(9)

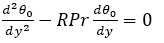(10)

Together with the set of boundary conditions:

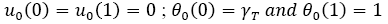(11)

First-order system :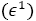

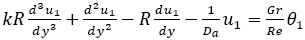
Under the assumption that 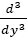is negligible the above equation reduces to,

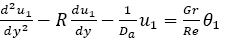(12)

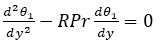(13)

Together with the set of boundary conditions,

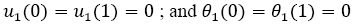(14)

Zeroth-order solution:

Solving equations (9) and (10) using the boundary conditions (11), we get,

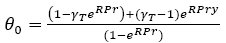(15)

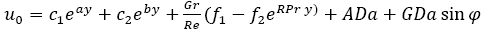(16)

Where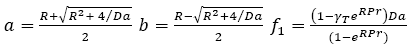

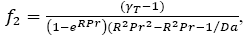
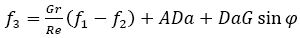
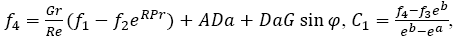
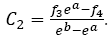
First order solution:

Solving equation (13) with boundary conditions, we obtain,

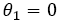(17)

Substituting equation (17) in the equation (12) and then solving the resulting equation with the corresponding conditions, we get,

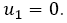
Results, Discussion and Conclusion

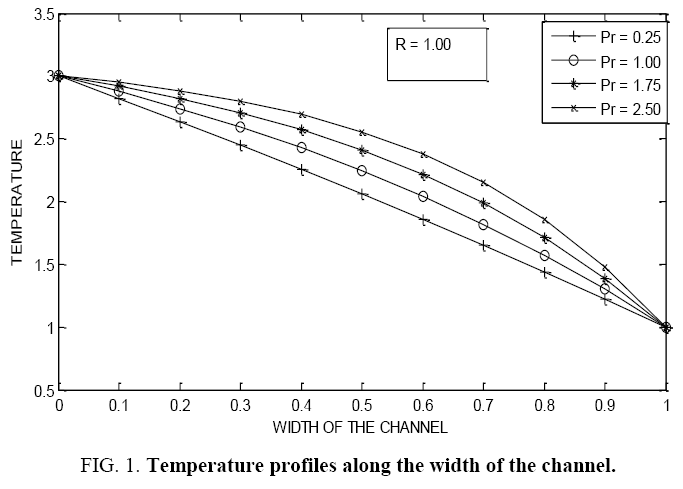
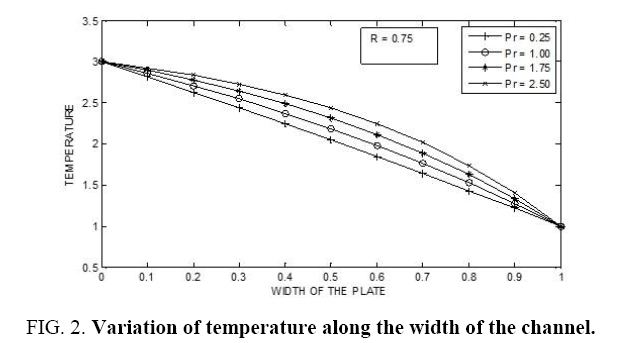
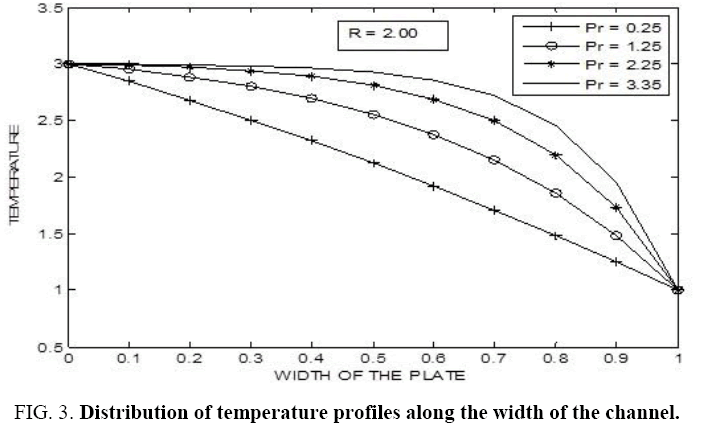
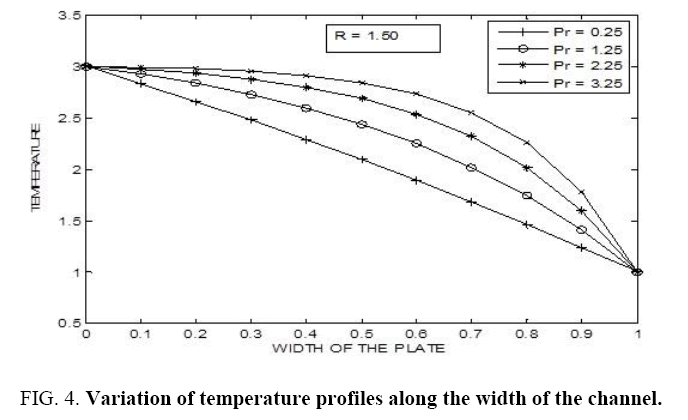
Figure 1-9 illustrates the variation of temperature with respect to Prandtl number for different values of radiation parameter. In each of these observations it is noticed that as a Prandtl number increases the temperature also increases. Not much of significant change is observed when the radiation parameter (R) is slightly decreased. However, a drastic change is noticed when the Prandtl number changes considerably along with the radiation parameter (R).

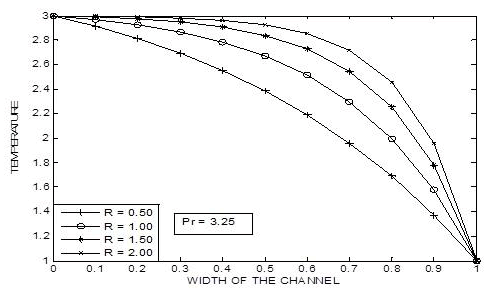
Figure 10 and Figure 11 demonstrates the distribution of temperature profiles in the fluid medium for different values of Prandtl number (Pr). In both of these illustrations it is observed that as we move far away from the lower boundary the temperature decreases. Further it is observed that as the radiation parameter (R) increases the temperature of the fluid decreases.

References

1. Darcy LesH.Fountaines Public of the city of Dijon, Victor Dultmont, Paris. 1856.
2. MurthyPVSN, SinghP. Thermal dispersion effects on non-Darcy natural convection with lateral mass flux. Heat and Mass Transfer.1977;33:1-5.
3. ChengP,MinkowyczW. Free convection about a vertical plate embedded in porous with application to heat transfer from a dike. J Geophy Res.1977;82:2040-9.
4. Donald M, EI-SayedIF, MowMS. Flow through porous medium the Ergun equation revisited. IndustChemFundam. 1979;18:199-208.
5. JosephDD, NieldDA,PapanicolaouG. Non-Linear equation governing flow in a saturated porous medium. Water Res Res. 1982;18:1049-52.
6. VafaiK,TienCL. Boundary and inertia effects on convective mass transfer in porous media. Int J Heat and Mass Transfer.1982;25:1183-90.
7. KnuppPM, LargeJL.Generali-zation of the Forchheimer-extended Darcy flow model to the tensor permiability case via a variational principle. J Fluid Mech. 1995;299:97-104.
8. MurthyPVSN. Thermal dispersion and viscous dissipation effects on non-Darcy mixed convection in a fluid saturated porous medium. Heat and Mass Transfer.1998;33:295-300.
9. Hassanien IA, BakierAY, GorlaRSR. Effects of thermal dispersion and stratification on non-Darcy mixed convection from a vertical plate in porous medium. Heat and Mass Transfer.1998;34:209-212.
10. Kuznetsov AV. Investigation of the effect of transverse thermal dispersion on forced convection in porous media. ActaMechania.2000;145:35-43.
11. MohammadienAA, El-AminMF. Thermal dispersion radiation effects on non-Darcy natural convection in a fluid saturated porous medium. Transport in porous media.2000;40:153-63.
12. Cheng WT,Hasio T. Lin, unsteady forced convection heat transfer on a flat plate embedded in the fluid saturated porous medium with inertia effect and thermal dispersion.IntJ Heat and Mass Trans.2002;45:1563-9.
13. Chamkha AJ, Mujtaba M, QuadriA. Simultaneous heat and mass transfer by natural convection from a plate embedded in a porous medium with thermal dispersion effects. Heat and Mass Transfer.2003;39:561-9.
14. WangC, LiaoSJ, ZhuJM. An explicit analytic solution for non-Darcy natural convection over horizontal plate with surface mass flux and thermal dispersion effects. ActaMechania.2003;165:139-50.