Original Article
, Volume: 15( 1)D-Radius and D-Diameter of Some Families of Graphs
- *Correspondence:
- Reddy Babu D Department of Mathematics(PPMat089), Rayalaseema University, Kurnool, India, Tel: +919441752543; E-mail: reddybabu17@gmail.com
Received: March 20, 2017 Accepted: April 10, 2017 Published: April 12, 2017
Citation: Reddy Babu D, Varma LNP. D-Radius and D-Diameter of Some Families of Graphs. Int J Chem Sci. 2017;15(1):116.
Abstract
The D-distance between vertices of a graph is obtained by considering the path lengths and as well as the degrees of vertices present on the path. In this article, we study the D-radius and D-diameter of some families of graphs with respect to D-distance. 2000 Mathematics Subject Classification: 05C12.
Keywords
D-distance; D-radius; D-diameter
Introduction
By a graph G=(V, E), we mean a finite undirected graph without loops and multiple edges. The concept of distance is one of the important concepts in study of graphs. It is used in isomorphism testing, graph operations, Hamilton city problems, extremal problems on connectivity and diameter, convexity in graphs etc. Distance is the basis of many concepts of symmetry in graphs [1].
In an earlier article authors introduced the concept of D-distance [2], by considering not only path length between vertices, but also the degrees of all vertices present in a path while defining the D-distance.
Preliminaries
Throughout this article, by a graph G(V, E) or simply G, we mean a non-trivial, finite, undirected graph without multiple edges and loops. Further all graphs we consider are connected [3].
Definition 2.1: If u, v are vertices of a connected graph G the D-length P of a u-v path S is defined as l(s)=d(u, v)+deg(u)+deg(v)+ deg(w) where sum runs over all intermediate vertices w of s.
Definition 2.2: (D-distance). The D − distance dD (u,v) between two vertices u,v of a connected graph G is defined as 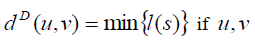 are distinct and
are distinct and 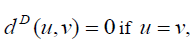 where the minimum is taken over all u − v paths s in G .
where the minimum is taken over all u − v paths s in G .
Definition 2.3: The D-eccentricity of any vertex v, eD (v) , is defined as the maximum distance from v to any other vertex, 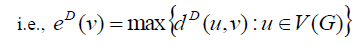
Definition 2.4: Any vertex u for which 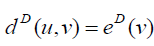 is called D eccentric vertex of v . Further, a vertex u is said to be D eccentric vertex of G if it is the D − eccentric vertex of some vertex.
is called D eccentric vertex of v . Further, a vertex u is said to be D eccentric vertex of G if it is the D − eccentric vertex of some vertex.
Definition 2.5: The D-radius, denoted by rD (G) , is the minimum D-eccentricity among all vertices of G i.e., 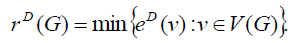 Similarly the D-diameter, dD (G) is the maximum D-eccentricity among all
vertices of G.
Similarly the D-diameter, dD (G) is the maximum D-eccentricity among all
vertices of G.
Definition 2.6: The D-center of G, CD (G) , is the sub graph induced by the set of all vertices of minimum D− eccentricity. A graph is called D-self-centered if CD(G) = G or equivalently rD (G) = dD(G). Similarly, the set of all vertices of maximum D-eccentricity is the D-periphery of G.
D-radius and D-diameter of families of graphs
There are some graphs for which D-radius and D-diameter are same, i.e., they are D-self-centered.
Theorem 3.1: For Complete graph, , Kn on n vertices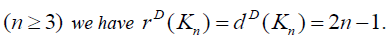
Proof: In complete graph Kn , degree of each vertex is n − 1.Thus D-distance between any two vertices is 1+ n-1+ n-1= 2n-1. Thus D-eccentricity of every vertex is 2n -1. Hence D-radius and D-diameter of Kn equal and is equal to 2n -1.
Theorem 3.2: For cycle graph, Cn ,with n vertices we have 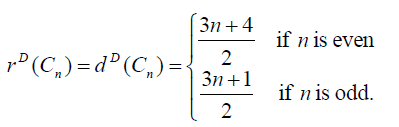
Proof: In cycle graph Cn, degree of each vertex is 2. the D-distance between the vertices is given below. We will consider even and odd cases separately.
Case 1: When n is even, the D-distance in Cn are as below.
 |
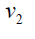 |
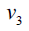 |
 |
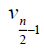 |
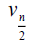 |
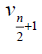 |
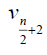 |
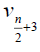 |
 |
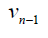 |
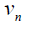 |
|
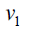 |
0 | 5 | 8 |  |
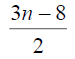 |
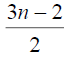 |
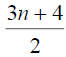 |
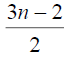 |
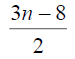 |
 |
8 | 5 |
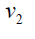 |
5 | 0 | 5 |  |
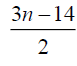 |
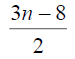 |
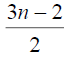 |
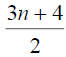 |
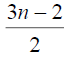 |
 |
11 | 8 |
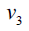 |
8 | 5 | 0 |  |
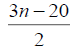 |
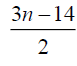 |
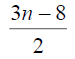 |
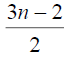 |
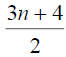 |
 |
14 | 11 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
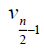 |
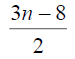 |
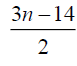 |
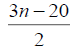 |
 |
0 | 5 | 8 | 11 | 14 |  |
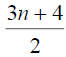 |
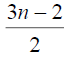 |
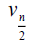 |
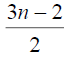 |
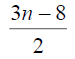 |
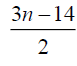 |
 |
5 | 0 | 5 | 8 | 11 |  |
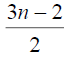 |
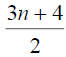 |
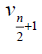 |
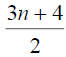 |
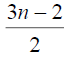 |
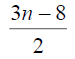 |
 |
8 | 5 | 0 | 5 | 8 |  |
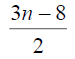 |
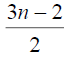 |
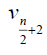 |
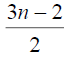 |
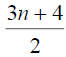 |
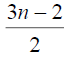 |
 |
11 | 8 | 5 | 0 | 5 |  |
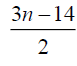 |
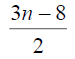 |
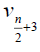 |
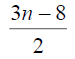 |
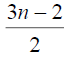 |
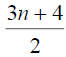 |
 |
14 | 11 | 8 | 5 | 0 |  |
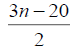 |
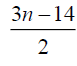 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
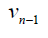 |
8 | 11 | 14 |  |
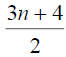 |
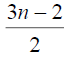 |
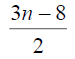 |
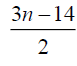 |
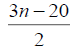 |
 |
0 | 5 |
 |
5 | 8 | 11 |  |
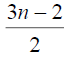 |
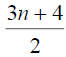 |
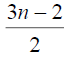 |
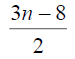 |
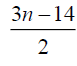 |
 |
5 | 0 |
Table 1. D-eccentricity of every vertex is 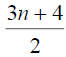 . Hence the D- radius and D-diameter is same, if n is even.
. Hence the D- radius and D-diameter is same, if n is even.
Case 2: When n is odd, the D-distance in Cn are as below
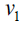 |
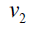 |
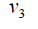 |
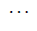 |
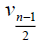 |
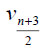 |
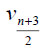 |
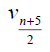 |
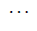 |
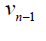 |
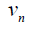 |
|
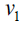 |
0 | 5 | 8 | 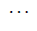 |
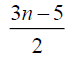 |
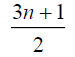 |
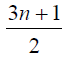 |
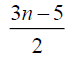 |
 |
8 | 5 |
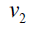 |
5 | 0 | 5 |  |
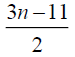 |
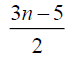 |
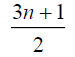 |
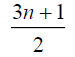 |
 |
11 | 5 |
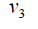 |
8 | 5 | 0 | 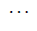 |
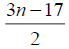 |
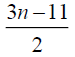 |
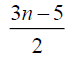 |
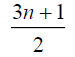 |
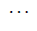 |
14 | 11 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
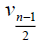 |
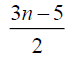 |
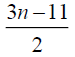 |
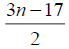 |
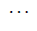 |
0 | 5 | 8 | 11 | 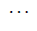 |
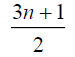 |
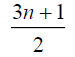 |
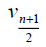 |
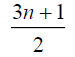 |
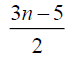 |
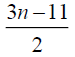 |
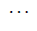 |
5 | 0 | 5 | 8 | 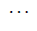 |
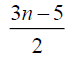 |
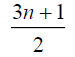 |
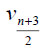 |
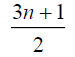 |
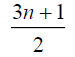 |
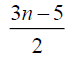 |
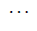 |
8 | 5 | 0 | 5 | 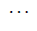 |
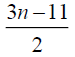 |
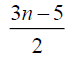 |
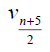 |
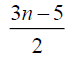 |
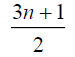 |
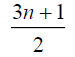 |
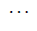 |
11 | 8 | 5 | 0 | 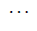 |
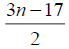 |
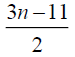 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
8 | 11 | 14 |  |
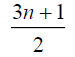 |
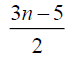 |
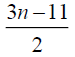 |
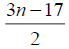 |
 |
0 | 5 |
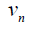 |
5 | 8 | 11 |  |
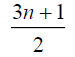 |
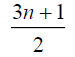 |
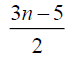 |
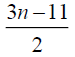 |
 |
5 | 0 |
Table 2. D-eccentricities of each vertex is 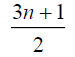 , if n is odd.
, if n is odd.
Hence D-radius and D-diameter is same. Thus 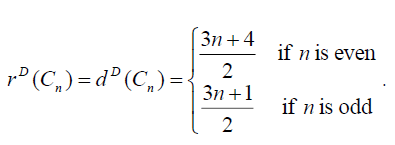
Next, we calculate D-radius and D-diameter of some families of graphs
Theorem 3.3: for complete biaparted graph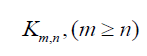 we have
we have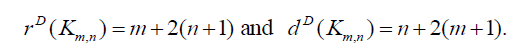
Proof: Without loss of generality assume that (m ≥ n) . N complete biparted graph Km,n degree of the vertices v1,v2,v3....vm is n and degree u1,u2,u3....un of the vertices m . Thus 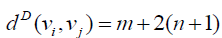
if 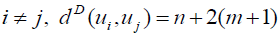 if
if 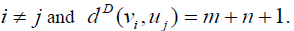
Therefore, 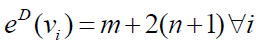 and
and 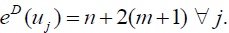 Hence the D-radius of Km,n is m + 2(n +1) and D-diameter of Km,n is n + 2(m + 1).
Hence the D-radius of Km,n is m + 2(n +1) and D-diameter of Km,n is n + 2(m + 1).
Theorem 3.4: For star graph, 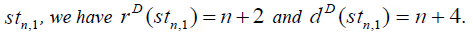
Proof: In star graph, stn,1 the degree of central vertex is n and degree of remaining vertices is 1. The D-distance from central vertex to other vertices is n + 2 and the D-distance between all other vertices is n + 4 Therefore the minimum Deccentricity is n + 2 and the maximum D-eccentricity is n + 4 Hence the D-radius of stn,1 is n + 2 of n + 4
Theorem 3.4: For path graph Pn , on n vertices (n ≥ 3) we have 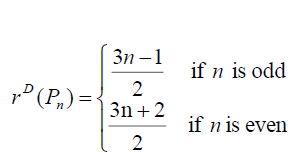 and
and 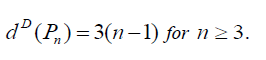 Further
Further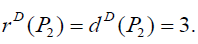
Proof: In path graph Pn , degree of end vertices is 1 and remaining vertices of degree is 2.
For 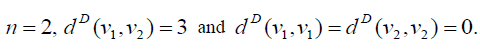 Thus the D-eccentricity of each vertex is 3. Hence the
D-radius and D-diameter of P2 are same and equal to 3.
Thus the D-eccentricity of each vertex is 3. Hence the
D-radius and D-diameter of P2 are same and equal to 3.
Next consider path graph with n ≥ 3. we can consider even and odd cases separately, in this case the D-distance between vertices are as given below.
Case 1: When n is odd, the D-distance in Pn are as below
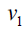 |
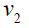 |
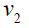 |
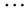 |
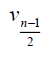 |
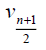 |
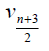 |
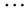 |
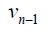 |
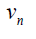 |
|
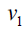 |
0 | 4 | 7 | 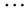 |
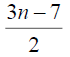 |
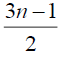 |
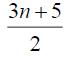 |
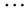 |
3n-5 | 3n-3 |
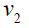 |
4 | 0 | 5 | 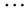 |
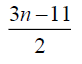 |
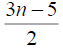 |
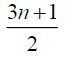 |
 |
3n-7 | 3n-5 |
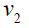 |
7 | 5 | 0 | 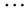 |
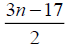 |
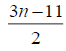 |
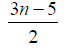 |
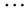 |
3n-10 | 3n-7 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
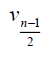 |
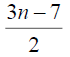 |
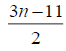 |
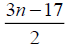 |
 |
0 | 5 | 8 |  |
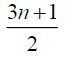 |
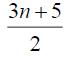 |
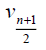 |
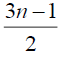 |
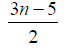 |
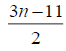 |
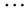 |
5 | 0 | 5 | 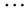 |
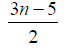 |
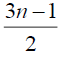 |
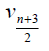 |
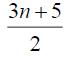 |
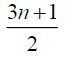 |
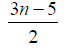 |
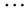 |
8 | 5 | 0 | 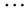 |
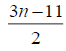 |
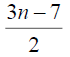 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
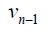 |
3n-5 | 3n-7 | 3n-10 | 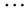 |
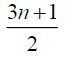 |
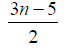 |
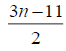 |
 |
0 | 4 |
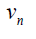 |
3n-3 | 3n-5 | 3n-7 | 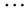 |
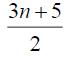 |
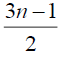 |
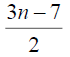 |
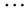 |
4 | 0 |
Table 3. D-eccentricities are 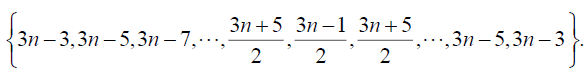
Thus the maximum D-eccentricity of Pn is 3n - 3 and minimum D-eccentricity is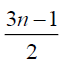 Hence the D-radius is
Hence the D-radius is 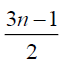 and the D-diameter is 3n - 3 if n is odd.
and the D-diameter is 3n - 3 if n is odd.
Case 2: When n is even, the D-distance in Pn are as below
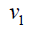 |
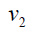 |
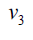 |
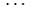 |
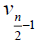 |
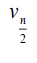 |
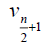 |
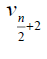 |
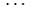 |
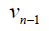 |
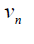 |
|
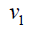 |
0 | 4 | 7 | 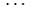 |
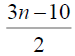 |
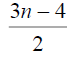 |
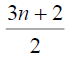 |
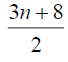 |
 |
3n-5 | 3n-3 |
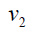 |
4 | 0 | 5 | 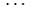 |
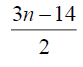 |
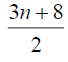 |
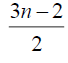 |
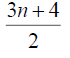 |
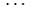 |
3n-7 | 3n-5 |
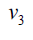 |
7 | 5 | 0 | 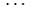 |
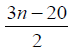 |
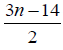 |
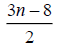 |
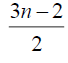 |
 |
3n-10 | 3n-7 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
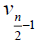 |
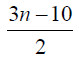 |
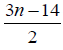 |
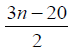 |
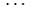 |
0 | 5 | 8 | 11 | 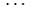 |
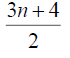 |
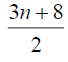 |
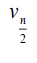 |
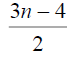 |
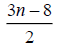 |
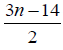 |
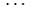 |
5 | 0 | 5 | 8 | 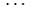 |
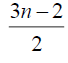 |
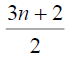 |
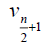 |
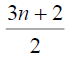 |
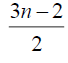 |
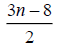 |
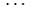 |
8 | 5 | 0 | 5 | 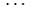 |
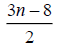 |
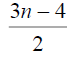 |
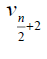 |
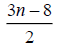 |
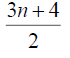 |
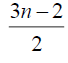 |
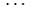 |
11 | 8 | 5 | 0 | 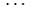 |
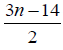 |
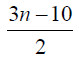 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
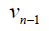 |
3n-5 | 3n-7 | 3n-10 | 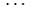 |
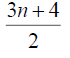 |
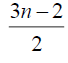 |
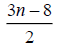 |
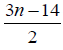 |
 |
0 | 4 |
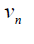 |
3n-3 | 3n-5 | 3n-7 | 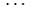 |
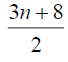 |
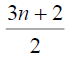 |
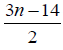 |
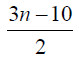 |
 |
4 | 0 |
Table 4. D-eccentricities are 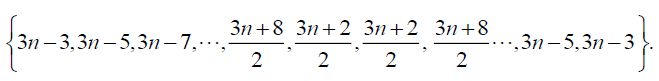
Thus the maximum D-eccentricity of Pn is 3n - 3 and minimum D-eccentricity is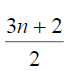 Hence the D-radius is
Hence the D-radius is 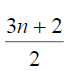 and the D-diameter is 3n - 3 if n is even.
and the D-diameter is 3n - 3 if n is even.
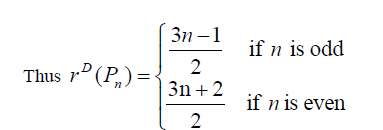
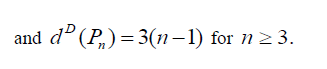
Theorem 3.5: For wheel graph, Wn,1 , with n + 1 vertices we have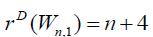 and
and 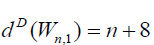 for n ≥ 6. Further we have
for n ≥ 6. Further we have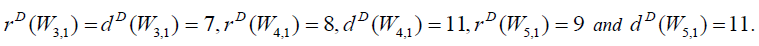
Proof: For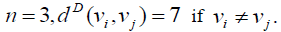 Thus the D-eccentricity of every vertex is 7. Hence the D-radius and Ddiameter
of W3,1 is 7 ( and hence W3,1 is self-centered ).
Thus the D-eccentricity of every vertex is 7. Hence the D-radius and Ddiameter
of W3,1 is 7 ( and hence W3,1 is self-centered ).
For 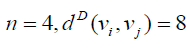 if vi is central vertex and
if vi is central vertex and 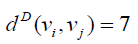 or 11, if vi is not central vertex. Thus the Deccentricity
central vertex is 8 and the D-eccentricity of other vertices is 11. hence the D-radius of W4,1 is 8 and Ddiameter
of W4,1 is 11.
or 11, if vi is not central vertex. Thus the Deccentricity
central vertex is 8 and the D-eccentricity of other vertices is 11. hence the D-radius of W4,1 is 8 and Ddiameter
of W4,1 is 11.
For 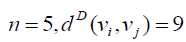 if vi is central vertex and
if vi is central vertex and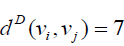 or 11, if i v is not central vertex. Thus the Deccentricity
central vertex is 9 and the D-eccentricity of other vertices is 11. hence the D-radius of W5,1 is 9 and Ddiameter
of W5,1 is 11.
or 11, if i v is not central vertex. Thus the Deccentricity
central vertex is 9 and the D-eccentricity of other vertices is 11. hence the D-radius of W5,1 is 9 and Ddiameter
of W5,1 is 11.
In wheel graph Wn,1 degree of central vertex is n and degree of remaining vertices is 3. Thus D-eccentricity of central vertex is n + 4 and D-eccentricity of remaining vertices is n + 8 for n ≥ 6. Thus the D-radius of Wn,1 is n + 4 and Ddiameter of Wn,1 is n + 8 for n ≥ 6.
