Original Article
, Volume: 10( 1)Computational Prediction of the Reactivity Sites of Alzheimer Amyloid b-Peptides Ab40 and Ab42
- *Correspondence:
- Daniel Glossman-Mitnik Department of Environment and Energy, NANOCOSMOS Virtual Laboratory, Chihuahua Industrial Complex, Mexico
Tel: +526144391151; E-mail: daniel.glossman@cimav.edu.mx
Received: March 13, 2017 Accepted: March 20, 2017 Published: March 23, 2017
Citation:Frau J, Glossman-Mitnik D. Computational Prediction of the Reactivity Sites of Alzheimer Amyloid b-Peptides Ab40 and Ab42. Chemxpress. 2017;10(1):120.
Abstract
Alzheimer’s illness is an advanced nervous syndrome that is connected to the existence of extracellular senile plaques. The extracellular senile plaques are predominantly composed of 40-42 residues of amino acid comprising polypeptides identified as b-peptides. The Theory of Chemical Reactivity together with MEDT (Molecular Electron Density Theory) and Conceptual DFT have been used to determine descriptors that permitted the forecast of the sites of reactivity of the Alzheimer amyloidb-Peptides Ab40 and Ab42 through QM:MM calculations with the ONIOM methodology.
Keywords
Alzheimer; Amyloid b-peptides; Ab40; Ab42; Computational chemistry; Molecular modeling; Conceptual DFT; Chemical Reactivity theory
Introduction
The non-enzymatic reaction between the amino groups of amino acids, peptides and proteins and reducing carbohydrates is referred to as glycation. A series of several reactions causes the AGEs (Advanced Glycation End products) formation. These molecules have been linked to certain illnesses such as diabetes, Parkinson and Alzheimer. The non-enzymatic glycation of proteins has been connected to the significant cause of the Alzheimer and diabetes ailment complications. It is recognized that glycation comprises of the reaction of the e-amino groups of the lysines present in the proteins.
The amino group immediate chemical environment controls the reaction of glycation. Some years ago, [1,2] studied several peptides of the Ab40 and Ab42 kind. The primary structure of these peptides is DAEFRHDSGYEVHHQKLVF-FAEDVGSNKGAIILGLMVGGVVIA. The major difference between these two peptides is the absence or presence of the C-terminal dipeptide (e.g. two hydrophobic residues Ile41-Ala42). The dipeptide has been described to make a significant effect on Ab(1-40) and Ab(1-42) oligomerization rates and mechanisms. Thus, it is critical to understand the molecular details of each species in early Ab combination for a coherent design of therapeutics to inhibit Alzheimer’s illness.
Therefore, it is considered necessary to develop a computational and theoretic tool that can be helpful in a forecast of the ideal sites of glycation for the diverse Ab peptides since they can assist in AGE inhibitors development [3]. The goal of this effort is studying the sites of glycation of the peptides through calculation of various Conceptual DFT descriptors such as the Fukui function indices, nucleophilic and electrophilic Parr functions and the condensed dual descriptor Df(r) [4]. As the preferred glycation sites, will be equivalent to the ones for the protonation reaction, the results of the calculations will permit us to qualitatively forecast the pKa variation of the lysine residues between the two peptides.
Theoretical Framework
As this work is part of an ongoing project, the theoretical background is similar to that presented in previous research [5-11] and will be shown here for the sake of completeness. The chemical potential m in the theoretical background of DFT is well defined as: 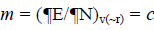 where c represents the electronegativity [12,13]. On the other hand, the global hardness h is:
where c represents the electronegativity [12,13]. On the other hand, the global hardness h is: 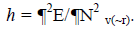 Through finite difference approximation, the two expressions may be written as: c=0.5 (I+A) and h=(I-A). I and A represents the ionization potential and electron affinity, respectively. The electrophilicity index w has been defined as [14]: w=m2/2h = (I+A)2/4(I A).
Through finite difference approximation, the two expressions may be written as: c=0.5 (I+A) and h=(I-A). I and A represents the ionization potential and electron affinity, respectively. The electrophilicity index w has been defined as [14]: w=m2/2h = (I+A)2/4(I A).
The electroaccepting (w+) and electrodonating (w) powers are stated as: [15] w+=(I+3A)2/16(I A) and w=(3I+A)2/16(I A). The larger value of w+ value corresponds to enhanced ability to accept charge, while a smaller value of w makes it an improved electron donor. The following net electrophilicity definition has been recommended [16] to make a comparison between w+ and w: Dw=w+ (w)=w++w, that is, a relation between the electro donating and electro accepting powers.
Settings and Computational Methods
Following the lines of our previous work, [5-11] the molecular structures of the amyloid b-peptides were optimized by starting with the readily available PDB structures), [17] and finding the most stable conformers by means of the Avogadro 1.2.0 program [18,19] through a random sampling technique with molecular mechanics and a consideration of all the torsional angles through the general AMBER force field [20].
The energies of the neutral, positive and negative peptides were obtained within the framework of QM:MM calculations performed through the ONIOM method [21] in the presence of water as a solvent, by doing IEF-PCM computations according to the SMD solvation model [22]. For the QM region, the MN12SX density functional [23] was selected in association with the Def2TZVP basis set [24,25]. All the ONIOM calculations were done and executed with the Gaussian 09 [26] series of programs.
Results and Discussion
Table 1 shows the ionization potentials I and electron affinities A (in eV), and global electronegativity c, total chemical hardness h, global electrophilicity w, electrodonating power, (w), electro accepting power (w+), and net electrophilicity Dw of the optimized conformers of the amyloid b-peptides Ab40 and Ab42 calculated with the ONIOM method (MN12SX/Def2TZVP:Amber) using water as solvent simulated with the SMD parameterization of the IEF-PCM model.
| Peptide | I | A | c | h | w | (w ) | (w+) | Dw |
|---|---|---|---|---|---|---|---|---|
| Ab40 | 6.412 | 0.137 | 3.275 | 6.275 | 0.855 | 3.739 | 0.464 | 4.202 |
| Ab42 | 6.410 | 0.238 | 3.324 | 6.172 | 0.895 | 3.838 | 0.514 | 4.352 |
Table 1. Ionization potentials I and electron affinities A (in eV), and global electronegativity c, total chemical hardness h, global electrophilicity w, electrodonating power, (w), electro accepting power (w+), and net electrophilicity Dw of the optimized conformers of the amyloid b-peptides Ab40 and Ab42 calculated with the ONIOM method (MN12SX/Def2TZVP:Amber) using water as solvent simulated with the SMD parameterization of the IEF-PCM model.
Within a molecule, the condensed Fukui functions may be used to define the chemical reactivity of each atom. The condensed Fukui functions are as follows: for nucleophilic attack, 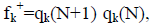 for electrophilic attack, fk=qk(N) qk(N 1), and for radical attack,
for electrophilic attack, fk=qk(N) qk(N 1), and for radical attack, 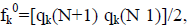 where qk represents the molecule’s gross charge of atom k. The definition of the condensed dual descriptor is
where qk represents the molecule’s gross charge of atom k. The definition of the condensed dual descriptor is 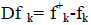 [27,28]. One can note from the analysis given by the Fukui function that the dual descriptor sign is significant to describe the site of reactivity in a molecule in the direction of an electrophilic or a nucleophilic attack. This means that the ideal reactivity sites for nucleophilic attack will be those associated to to Dfk>0, while for the case of electrophilic attack, the direction will be favored by Dfk<0 [27-29].
[27,28]. One can note from the analysis given by the Fukui function that the dual descriptor sign is significant to describe the site of reactivity in a molecule in the direction of an electrophilic or a nucleophilic attack. This means that the ideal reactivity sites for nucleophilic attack will be those associated to to Dfk>0, while for the case of electrophilic attack, the direction will be favored by Dfk<0 [27-29].
In 2014, Domingo proposed the Parr functions P(r) [30,31] which are given by the following expressions: P (r) = rrcs(r) (for electrophilic attacks) and P+(r)=rras(r) (for nucleophilic attacks), which are related to the atomic spin density (ASD) at the r atom of the radical cation or anion of a given molecule, respectively. The ASD over each atom of the radical cation and radical anion of the molecule gives the local nucleophilic Pk and electrophilic P+k Parr functions of the neutral molecule [32].
Table 2 shows the condensed Fukui functions fk, condensed dual descriptors D fk and electrophilic Parr functions Pk f over the N atoms of the amino groups of the Lys residues of the amyloid Ab40 and Ab42 peptides calculated with the ONIOM method (MN12SX/Def2TZVP:Amber) using water as solvent simulated with the SMD parameterization of the IEF-PCM model are presented in Table 2.
| Peptide | MPA | HPA | ||||
|---|---|---|---|---|---|---|
| fk | D fk | Pk | fk | D fk | Pk | |
| Ab40 | 0.718 | -0.718 | 0.804 | 0.633 | -0.633 | 0.776 |
| Ab42 | 0.717 | -0.722 | 0.804 | 0.633 | -0.640 | 0.776 |
Table 2. The condensed Fukui functions fk, condensed dual descriptors D fk and electrophilic Parr functions Pk f over the N atoms of the amino groups of the Lys residues of the amyloid Ab40 and Ab42 peptides calculated with the ONIOM method (MN12SX/Def2TZVP:Amber) using water as solvent simulated with the SMD parameterization of the IEF-PCM model. MPA: Mulliken Population Analysis-HPA: Hirshfeld Population Analysis.
From the examination of the results on Tables 1 and 2, it can be concluded that there are not significative differences in the chemical reactivity of both peptides. Nevertheless, the sites for glycation will be also the preferred sites for protonation. Therefore, the pKa’s of the Lys residues will also be reliant on the peptides conformational structures. Moreover, the trend in the pKa of the different conformers may be predicted in terms of the local hyper softness (LHS), which is a local reactivity descriptor that has been defined so that it permits to measure local reactivities according to the size of the molecule [33,34]. The equation is expressed as LHS D f (r)/h2 D f (r) S2 where S represents the global softness [4,35,36].
As the local hyper softness can be condensed over the atomic sites, the condensed local hyper softness is simply computed as LHS ' f+k fk (I A)2.
By considering the values for the condensed dual descriptor Dfk from Table 2 and the values for the chemical hardness h from Table 1, it can be predicted that the pKa of the Lys residue of Ab42 will be slightly higher than the pKa of the corresponding site of Ab40. This difference can be attributed to the presence of the C-terminal dipeptide and may be linked to the mechanisms and the rates of Ab (1-40) and Ab (1-42) oligomerizations.
Conclusions
In this paper, the reactivity sites of Alzheimer’s amyloid b peptides Ab40 and Ab42 have been forecasted and determined through the application of the Chemical Reactivity Theory, Conceptual DFT, and molecular electron density theory (MEDT). Amyloid b-peptides are dominant components of the extracellular senile plaques which is an indication of the Alzheimer’s illness. Additionally, this paper has looked at the structure and the participation of Ab40 and Ab42 peptides in glycation, their sites of glycation, and the oligomerization rate and mechanisms so as to gain an understanding of their role in Alzheimer’s illnesses. Partly, the motivation for the determination of the chemical reactivity sites was to inform about the development of AGE inhibitors.
The determination of the chemical reactivity sites was made possible through the computation of the QM:MM calculations using the ONIOM method with water acting as a solvent. The method was also used to calculate the energies of the positive, negative, and neutral peptides. The MN12SX density functional was selected in the QM region and for the MM region the Amber force field was considered and the calculations were done in accordance with the Gaussian 09 program.
From the whole of the results presented in this work, it can be seen that the sites of interaction of the amyloid b-peptides Ab40 and Ab42 can be predicted by using DFT-based reactivity descriptors such as the electronegativity, global chemical hardness, global electrophilicity, electrodonating and electroaccepting powers, net electrophilicity as well as Fukui functions, condensed dual descriptors, Parr functions and local hyper softness LHS. These descriptors were used in the characterization and successfully description of the preferred reactive sites and provide a firm explanation for the reactivity of those molecules, as well as about the pKa variation of the corresponding Lys residues of the two peptides.
Acknowledgement
This work has been partially supported by CIMAV, SC and National Council for Science and Technology (CONACYT, Mexico) through Grant 219566/2014 for Basic Science Research and Grant 265217/2016 for a Foreign Sabbatical Leave. Daniel Glossman-Mitnik con-ducted this work while a Sabbatical Fellow at the University of the Balearic Islands from which support is gratefully acknowledged. This work was cofunded by the Ministry of Economy and Competitiveness (MINECO) and the European Fund for Regional Development (FEDER) (CTQ2014-55835-R).
References
- Triguero L, Singh R, Prabhakar R. Comparative molecular dynamics studies of wild-type and oxidized forms of full-length Alzheimer amyloid β-peptides Aβ (1-40) and Aβ (1-42). J Phys Chem B. 2008;112(23):7123-31.
- Lee C, Ham S. Characterizing amyloid?beta protein misfolding from molecular dynamics simulations with explicit water. J Comput chem. 2011;32(2):349-55.
- Riek R, Güntert P, Döbeli H, et al. NMR studies in aqueous solution fail to identify significant conformational differences between the monomeric forms of two Alzheimer peptides with widely different plaque?competence, Aβ (1-40) ox and Aβ (1-42) ox. Eur J Biochem. 2001;268(22):5930-6.
- Parr RG. Density functional theory of atoms and molecules. In horizons of quantum chemistry 1980 (pp. 5-15). Springer Netherlands.
- Glossman-Mitnik D. A comparison of the chemical reactivity of naringenin calculated with the M06 family of density functionals. Chem Cent J. 2013;7(1):155-61.
- Martínez-Araya JI, Salgado-Mora?n G, Glossman-Mitnik D. Computational nanochemistry report on the oxicams conceptual DFT Indices and chemical reactivity. J Phys Chem B. 2013;117(21):6339-51.
- Glossman-Mitnik D. Computational study of the chemical reactivity properties of the Rhodamine B molecule. Procedia Comput Sci. 2013;18:816-25.
- Martínez-Araya JI, Salgado-Morán G, Glossman-Mitnik D. Computational Nutraceutics: Chemical reactivity properties of the flavonoid naringin by means of conceptual DFT. J Chem. 2013;2013:1-8.
- Glossman-Mitnik D. Chemical reactivity theory within DFT applied to the study of the prunin flavonoid. Eur Int J Sci Technology. 2014,3:195-207.
- Glossman-Mitnik D. Computational chemistry of natural products: A comparison of the chemical reactivity of isonaringin calculated with the M06 family of density functionals. J Mol model. 2014;20(7):2316.
- Frau J, Muñoz F, Glossman-Mitnik D. A molecular electron density theory study of the chemical reactivity of Cis-and trans-resveratrol. Molecules. 2016;21(12):1650.
- Parr RG, Yang W. Density functional approach to the frontier-electron theory of chemical reactivity. J Am chem soc. 1984;106(14):4049-50.
- Geerlings P, de Proft F, Langenaeker W. Conceptual density functional theory. Chem rev. 2003;103(5):1793-874.
- Parr R, Szentpaly L, Liu S. Electrophilicity index. J Am chem soc. 1999;121:1922-4.
- Gázquez JL, Cedillo A, Vela A. Electrodonating and electroaccepting powers. J Phys Chem A. 2007;111(10):1966-70.
- Chattaraj PK, Chakraborty A, Giri S. Net electrophilicity. J Phys Chem A. 2009;113(37):10068-74.
- Berman H, Henrick K, Nakamura H. Announcing the worldwide protein data bank. Nat Struct Mol Biol 2003;10(12):980.
- Avogadro [internet]. An Open-Source Molecular Builder and Visualization Tool-Version 1.2.0 [cited on: 2016, Dec 02]. Retrieved from: [http://avogadro.openmolecules.net.]
- Hanwell MD, Curtis DE, Lonie DC, et al. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J Chem inform. 2012;4(1):17.
- Wang J, Wolf RM, Caldwell JW, et al. Development and testing of a general amber force field. J comput Chem. 2004;25(9):1157-74.
- Chung LW, Sameera WM, Ramozzi R, et al. The ONIOM method and its applications. Chem Rev. 2015;115(12):5678-796.
- Marenich AV, Cramer CJ, Truhlar DG. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. The J Phys Chem B. 2009;113(18):6378-96.
- Peverati R, Truhlar DG. Screened-exchange density functionals with broad accuracy for chemistry and solid-state physics. phys chem ch ph. 2012;14(47):16187-91.
- Weigend F, Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. phys chem ch ph. 2005;7(18):3297-305.
- Weigend F. Accurate Coulomb-fitting basis sets for H to Rn. phys chem ch ph. 2006;8(9):1057-65.
- Frisch MJ, Trucks GW, Schlegel HB, et al. Gaussian 09 Revision D.01. Gaussian Inc., Wallingford CT, 2009.
- Morell C, Grand A, Toro-Labbé A. New dual descriptor for chemical reactivity. J Phys Chem A. 2005;109:205-12.
- Morell C, Grand A, Labbé AT. Theoretical support for using the Δf(r) descriptor. Chem phys lett. 2006;425(4):342-6.
- Gázquez JL. In chemical reactivity theory: A density functional view; Chattaraj P. K Ed. CRC Press-Taylor and Francis Group: Boca Raton, Fl. 2009; Chapter 2, pp 7-21.
- Domingo LR, Pérez P, Sáez JA. Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions. RSC Advances. 2013;3(5):1486-94.
- Chamorro E, Pérez P, Domingo LR. On the nature of Parr functions to predict the most reactive sites along organic polar reactions. Chem phys lett. 2013;582:141-3.
- Domingo LR, Ríos-Gutiérrez M, Pérez P. Applications of the conceptual density functional theory indices to organic chemistry reactivity. Molecules. 2016;21(6):748.
- Ayers PW, Morell C, De Proft F, Geerlings P. Understanding the Woodward-Hoffmann rules by using changes in electron density. Chem-Eur J. 2007 Oct 5;13(29):8240-7.
- Cárdenas C, Rabi N, Ayers PW, et al. Chemical reactivity descriptors for ambiphilic reagents: Dual descriptor, local hypersoftness, and electrostatic potential. J Phys Chem A. 2009;113(30):8660-7.
- Pearson RG. The principle of maximum hardness. Chemical Hardness. 1993;1:99-124.
- Chermette H. Chemical reactivity indexes in density functional theory. J comput chem.1999;20(1):129-54.
